A radius, generally denoted |r,| is a segment that joins any point of a circle to its centre.
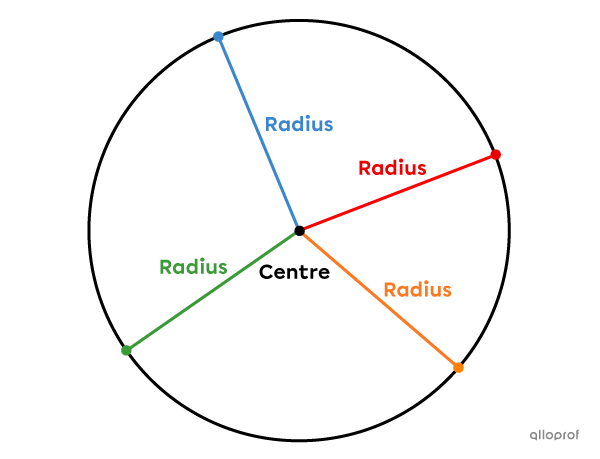
Since the circle is made of an infinite number of points, it has an infinite number of radii.
Extending a radius beyond the centre to join another point on the circle creates a diameter.
A diameter, generally denoted |d,| is a segment which connects 2 points of the circle and passes through the centre.
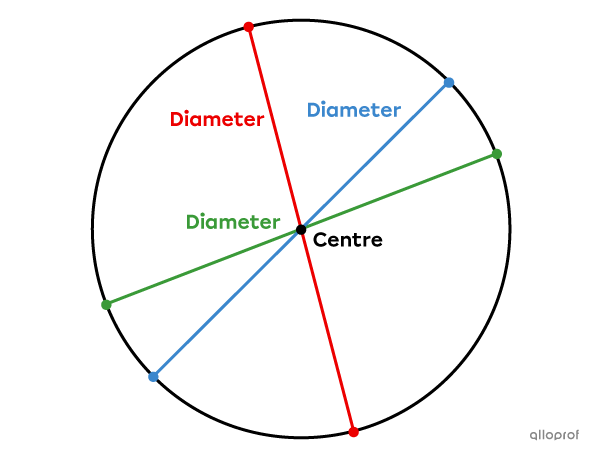
Since the circle has an infinite number of radii, it also has an infinite number of diameters.
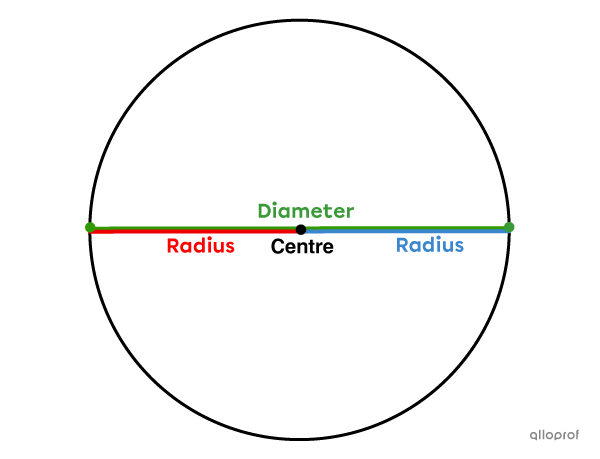
Since the radii and diameters pass through the centre of the circle, it is possible to find a relationship between these two measurements. In fact, the measure of the diameter is double the measure of the radius.
||d=2r\ \ \text{or}\ \ r=\dfrac{d}{2}||
A chord is a segment that connects any 2 points of the circle without necessarily passing through the centre.
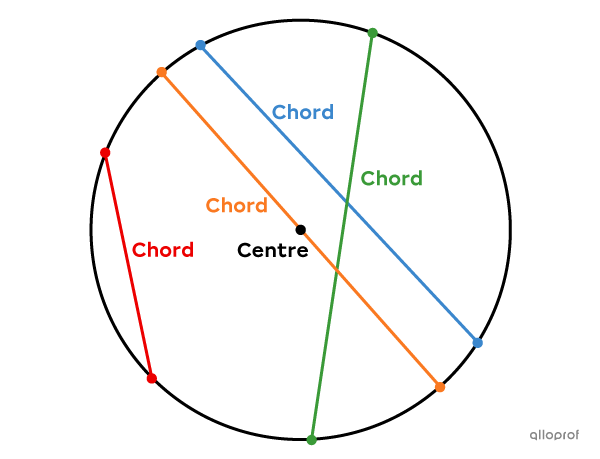
From this definition, we can deduce that a diameter is a chord, but not a radius. The diameter is in fact the longest chord of the circle.
Moreover, since the circle is composed of an infinite number of points, it also contains an infinite number of chords.
A central angle is formed by 2 radii.
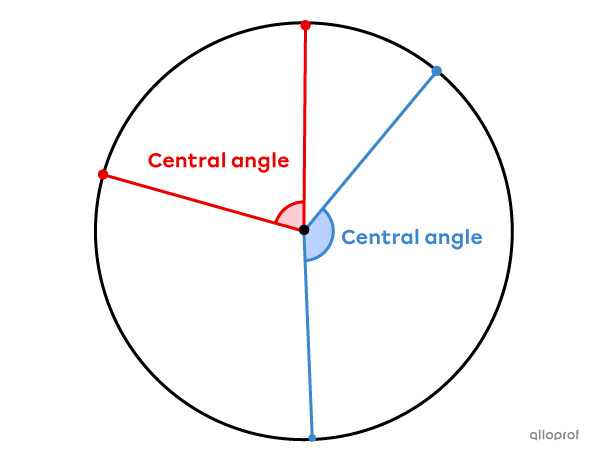
The measure of an angle at the centre is usually expressed as a value between |0^\circ| and |360^\circ.| Its vertex is at the centre of the circle.
The concept of a central angle is related to that of an arc of a circle and a circle sector. In fact, the central angle makes it possible to define a portion of the circle.
The circumference, generally denoted |C,| is the perimeter of a circle.
It is possible to unroll the circle to measure its circumference.
Note: The term perimeter refers to the outline of all plane figures, but the term circumference applies only to circles.
To calculate the circumference of a circle, we must use a formula that includes the measure of its radius or that of its diameter.
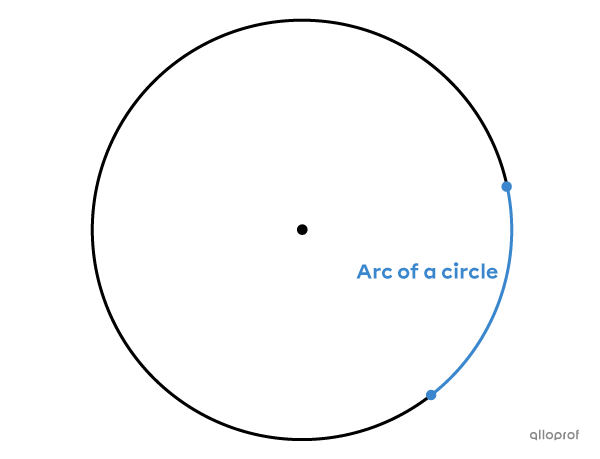
An arc of a circle is a portion of the circumference.
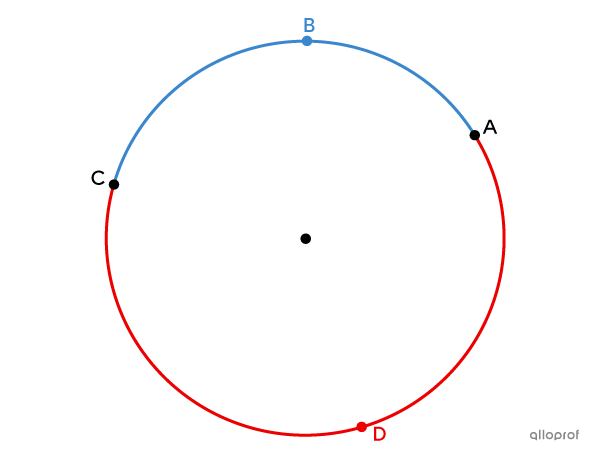
Does |\overset{\huge\frown}{AC}| refer to the arc that passes through point |B| or to the arc that passes through point |D|? To name an arc of a circle, we use the points that bound it. However, to avoid confusion, we sometimes add a 3rd letter to the name of an arc. In the following figure, we have 2 arcs of a circle: |\color{#3b87cd}{\overset{\Huge\frown}{ABC}}| and |\color{#ec0000}{\overset{\Huge\frown}{ADC}}.|
To find the measure of an arc of a circle, you must know the measure of the central angle that is associated with it.
The interior space of a circle refers to its area.
The area refers to the closed region inside the circle.
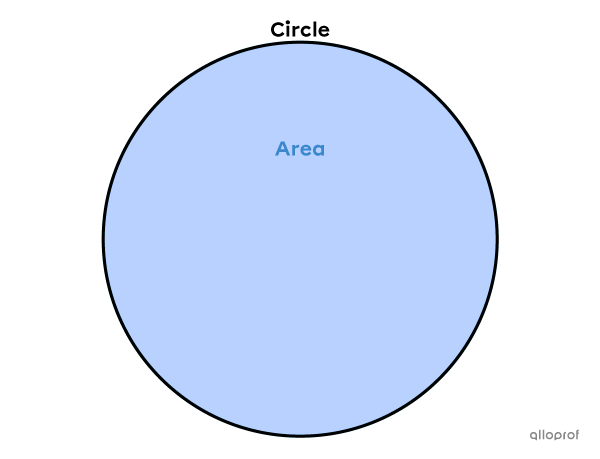
To calculate the area of a circle, we must use a formula that involves the measure of its radius.
A circle sector is a region bounded by an arc of a circle and 2 radii.
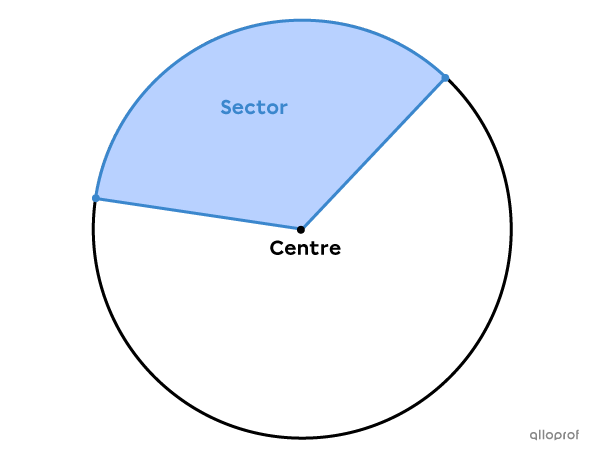
In other words, the circle sector is a fraction of the total area of the circle. To find its area, it is possible to determine a proportion with the total area of the circle.
In statistics, sectors are used to create pie charts.
An inscribed angle is formed by 2 chords and its vertex is located on the circle.
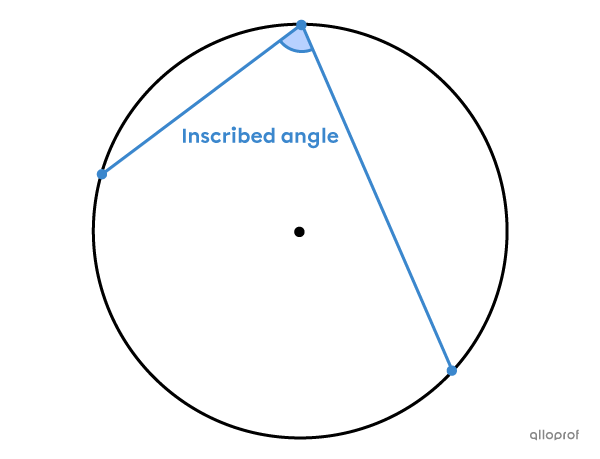
The vertex of the inscribed angle is on the circle and its sides intersect an arc of the circle.
To find the measure of an inscribed angle or the measure of the arc that is intersected, we use metric relations in the circle.
An inscribed circle is a circle tangent to all sides of a polygon.

In other words, it is the largest circle that lies inside a polygon. The circle must have a point in common with each side of the polygon. We can construct an inscribed circle using a method involving bisectors.
In regular polygons, we associate the radius of the circle with the apothem of the regular polygon.
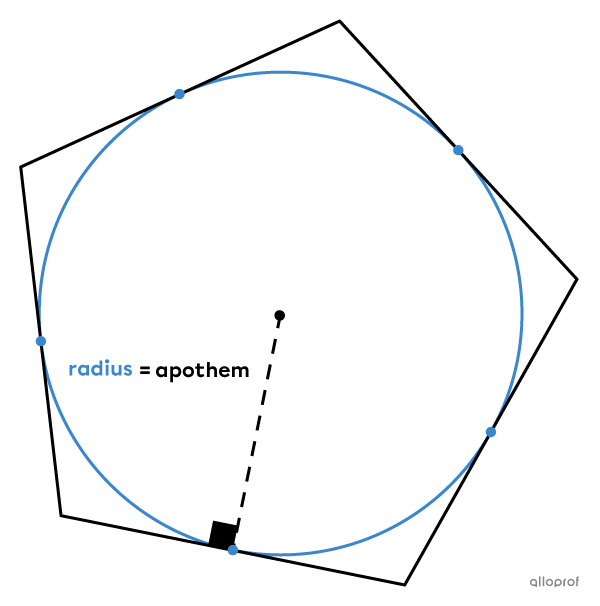
A circumscribed circle is a circle that passes through all the vertices of a polygon.

Unlike the inscribed circle, the circumscribed circle lies outside the polygon. We can construct a circumscribed circle using a method involving the medians.
In regular polygons, the radii of the circle are associated with the congruent sides of the isosceles triangles that compose it.

A tangent to a circle is a line that touches the circle at a single point. This line is perpendicular to the radius of the circle that passes through the point.
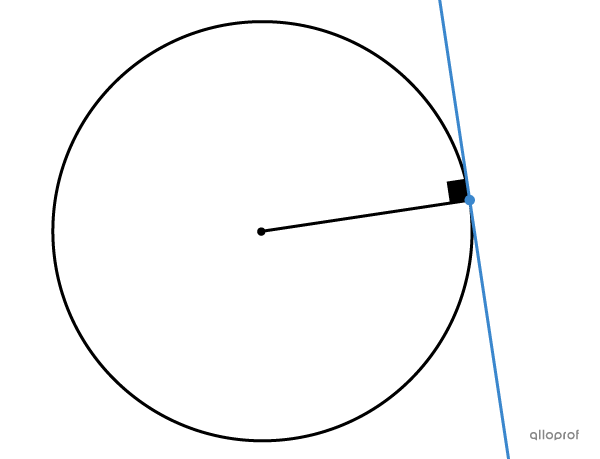
Analytic geometry is used to determine the equation of a tangent to a circle.
Pour réviser des notions de géométrie, joue à La foire.
