Once each of the geometric transformations have been mastered, they can be used with the same initial figure. In this case, it becomes a composition of transformations.
A composition of transformations is a sequence of transformations.
In terms of notation, for example, |t \circ s| is written "|t| composite |s|" and it means we must perform the reflection first and the translation second. In short, geometric transformations must be carried out from right to left.
It is important to follow the composition order presented to acquire the desired image figure.
According to the following drawing:
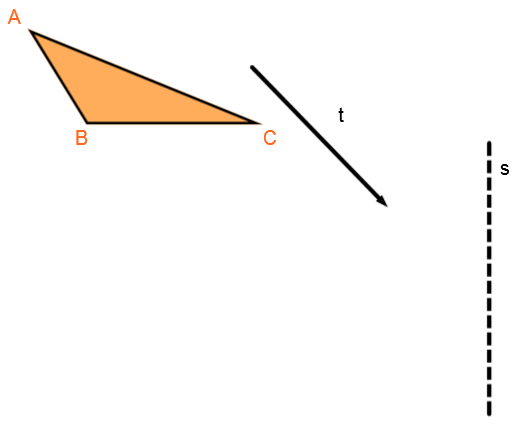
Perform the composition of transformations |s\circ t|
-
Identify the transformation order
Perform the translation |t| and apply a reflection across the axis |s|. -
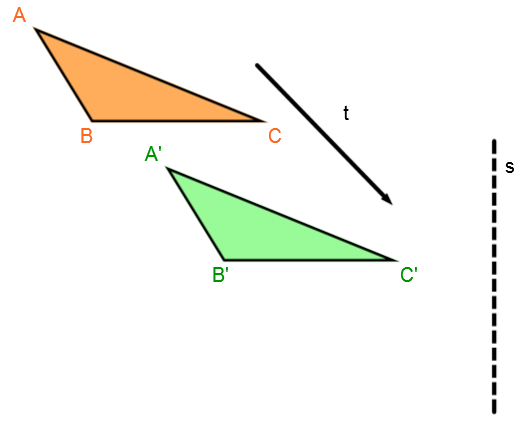
Perform the first transformation
Perform the translation |t| on the initial figure.
-
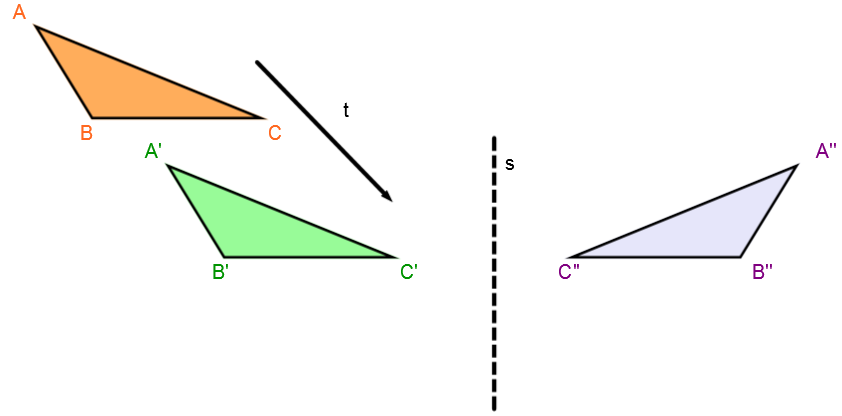
Perform the second transformation
Perform the reflection on the transformation image and not on the initial figure.
Among all the possible combinations, one has a particular name.
When a composition is made up of a translation and a reflection, and the translation arrow is parallel to the axis of reflection, the composition is called a glide reflection.
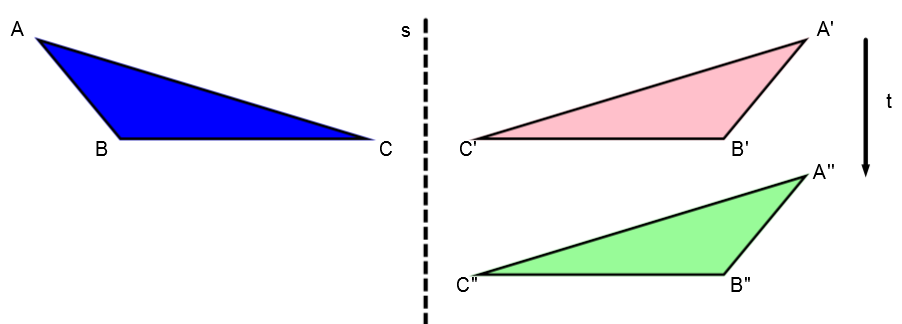
In this example, the axis of symmetry |s| is parallel to the translation arrow |t|.
To distinguish between the four basic geometric transformations, observe their properties.
