Une fois que l'on maîtrise chacune des transformations géométriques, on peut les utiliser avec une même figure initiale. Dans ce cas, il est question de composition de transformations.
Une composition de transformations est tout simplement un enchaînement de transformations.
Au niveau de sa notation, par exemple, |t \circ s| est lu «|t| rond |s| » et signifie qu'il faut faire la symétrie en premier et la translation en deuxième. Bref, il faut réaliser les transformations géométriques de la droite vers la gauche.
Il est important de bien suivre la chronologie de la composition présentée afin d'arriver à la figure image voulue.
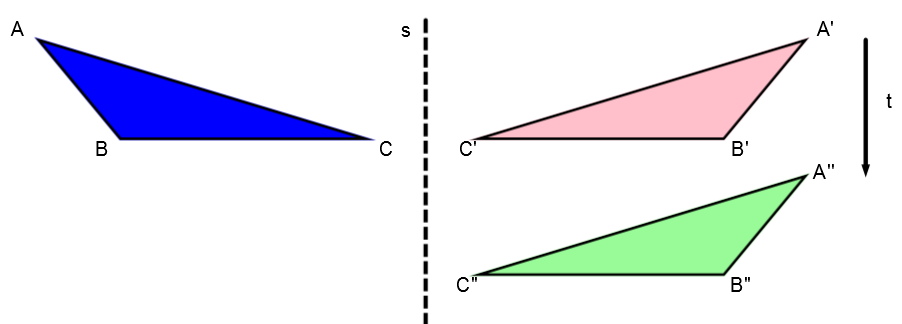
Selon le dessin suivant:
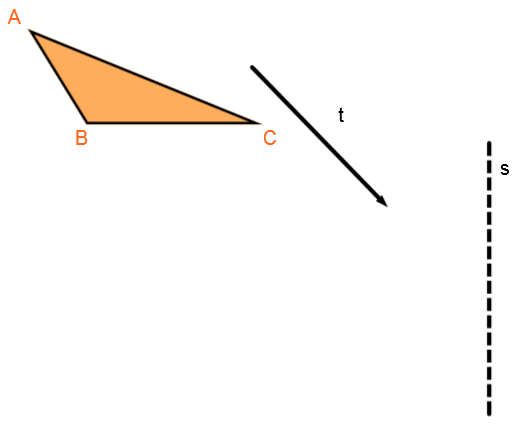
Réalise la composition de transformations |s\circ t|
1) Identifier la chronologie des transformations
On doit d’abord effectuer la translation |t| puis appliquer la symétrie par rapport à l'axe |s|.
2) Effectuer la première transformation
Pour cette étape, il faut effectuer la translation |t| sur la figure initiale.
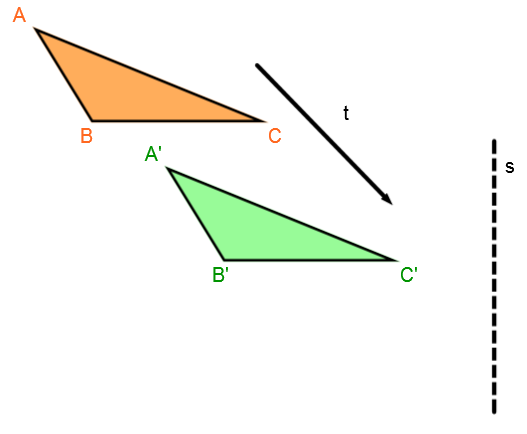
3) Effectuer la deuxième transformation
Pour cette étape, il faut effectuer la réflexion sur l'image de la première transformation et non sur la figure initiale.
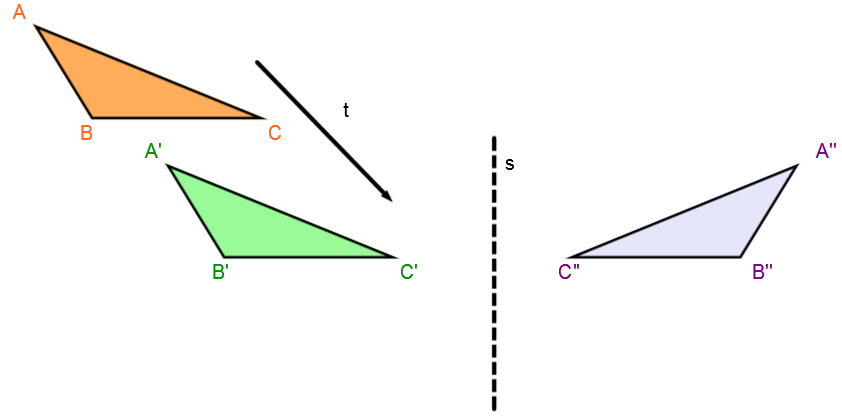
Parmi toutes les combinaisons possibles, il y en a une qui possède un nom particulier.
Lorsqu'une compositifion est formée d'une translation et d'une réflexion et que la flèche de translation est parallèle à l'axe de réflexion, cette composition se nomme une symétrie glissée.
Dans cet exemple, l'axe de symétrie |s| est parallèle à la flèche de translation |t.|
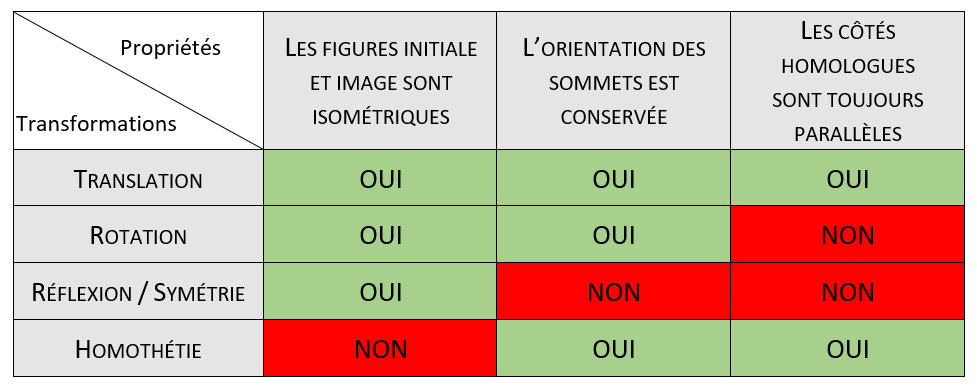
Pour distinguer les quatre transformations géométriques de base, on peut se fier à leurs propriétés.