The Perfect Square Trinomial

Factoring a perfect square trinomial is a technique for factoring a trinomial in the form of a squared binomial.

To be classified as a perfect square trinomial, the trinomial must have the following characteristics.

1. The first and third terms must be squares.

2. Regardless of the sign, the middle term must be equal to twice the product of the square roots of the first and third terms. ||\text{2}^\text{nd} \text{ term} = \pm \ 2\times \sqrt {a^2}\times \sqrt {b^2}=2ab||
   
   When factoring a perfect square trinomial, we obtain two identical factors that can be simplified into the form of a single squared binomial.||a^2\color{red}{+}2ab+b^2=(a\color{red}{+}b)(a\color{red}{+}b)=(a\color{red}{+}b)^2\\ \text{or } \\ a^2\color{red}{-}2ab+b^2=(a\color{red}{-}b)(a\color{red}{-}b)=(a\color{red}{-}b)^2||

A perfect square trinomial is a trinomial of the form: ||a^2\color{red}{+}2ab+b^2||or:||a^2\color{red}{-}2ab+b^2||

To factor a perfect square trinomial, we can follow these steps.

1. Find the square root of the 1^st and 3^rd terms, if possible. ||\sqrt{a^2}=\color{green}{a} \ \ \ \ \ \ \sqrt{b^2}=\color{blue}{b}||

2. Check if the 2^nd term, regardless of the value of its sign, corresponds to twice the product of |\color{green}{a}| and |\color{blue}{b}.| ||\text{2}^\text{nd} \text{ term}=2\color{green}{a}\color{blue}{b}||

3. Write the squared binomial using the results obtained in step 1, separated by the sign of the 2^nd term. ||(\color{green}{a}\color{red}{\pm} \color{blue}{b})^2||

Consider the following trinomial: |4x^2 +12xy + 9y^2|.

1. Find the square root of the first and third terms.
   ||\sqrt {4x^2} = \color{green}{2x}\ \text{ and }\ \sqrt {9y^2} = \color{blue}{3y}||
2. Check if the second term, regardless of its sign, corresponds to twice the product of |a| and |b|. ||\begin{align} \text{2}^\text{nd} \text{ term}&=2ab\\ 12xy&=2(\color{green}{2x})(\color{blue}{3y})\\ 12xy&=12xy \end{align}|| Since the verification works out, the trinomial is indeed a perfect square trinomial.
3. Write the squared binomial using the results obtained in step 1, separated by the sign of the 2^nd term.
   
   Sign of the second term: |\color{red}{+}| ||(\color{green}{2x}\color{red}{+}\color{blue}{3y})^2||

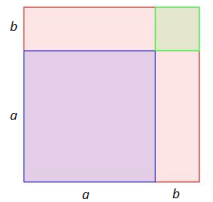
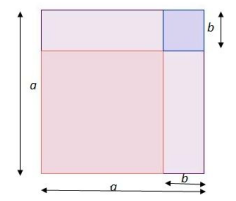
Here is a geometric representation of the two identities.

​|a^2+2ab+b^2=(a+b)^2|	​​|a^2-2ab+b^2=(a-b)^2|
The purple square has an area of |a^2,| the two rectangles each have an area of |ab|, and the green square has an area of |b^2.| The total area of ​​the 4 figures that make up the large square is:  ||a^2+ab+ab+b^2=a^2+2ab+b^2|| Since the side of the large square measures |a+b,| its area is |(a+b)^2.| The conclusion is the following. ||a^2+2ab+b^2=(a+b)^2||	The area of ​​the square in the bottom left can be obtained 2 different ways. The area of ​​the rectangle at the top whose length is the entire length of the figure is |ab|, just like the rectangle on the right whose height is the entire height of the figure. So, to get the area of ​​the square at the bottom left, we take the area of ​​the entire square |(a^2)| and subtract the area of ​​the two long rectangles. By subtracting like this, the area of the little blue square is removed twice instead of once. We therefore need to add the area of ​​this square |(b^2)| to compensate. Therefore, the area of ​​the square on the left is the following. ||a^2-ab-ab+b^2=a^2-2ab+b^2|| Since the measurement of the side of this same square is |a-b|, its area is |(a-b)^2|. By combining the 2 different ways, the identity can be written as follows. ||a^2-2ab+b^2=(a-b)^2||