When searching for the length of a contour or the measure of the interior surface of a plane figure, we can use different formulas to help. However, it is important to distinguish between the concepts of perimeter and area.
When a plane figure is formed by either broken or curved lines, it is possible to calculate the total length of the lines that form the contour.
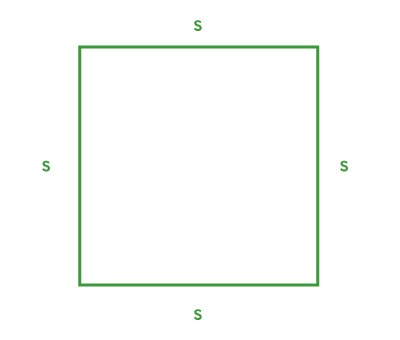
The perimeter (generally denoted by |P|) is the measure of the contour of a figure. To calculate it, we add together the measures of all the sides. In the case of a circle, the measure of the contour is called the circumference and is denoted by |C.|
Perimeter is expressed using measurement units such as |cm| and |m.|
To determine the total length of a fence for an enclosure, we must measure the length of the broken line forming the contour. Therefore, we must calculate the perimeter.
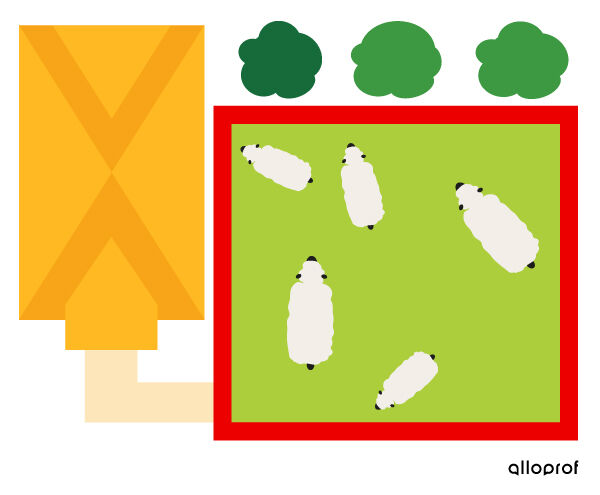
While the perimeter refers to the contour (outline) of a figure, the area refers to its surface.
Area (generally denoted as |A|) is the measure of the surface inside a plane figure.
Area is expressed using squared measurement units, such as |cm^2| and |m^2.|
To determine the price of the land, we start by calculating the area, i.e., the measure of the area of the land.
Pour valider ta compréhension de l'aire et du périmètre des figures planes de façon interactive, consulte la MiniRécup suivante :

Pour valider ta compréhension des mesures manquantes dans les figures planes de façon interactive, consulte plutôt la MiniRécup suivante :

To calculate the perimeter or the area, we can use different formulas.
|
Plane Figure |
Perimeter |
Area |
|---|---|---|
|
|P=\color{#3A9A38}{a}+\color{#3B87CD}{b}+\color{#FF55C3}{c}| |
|A=\dfrac{\color{#3B87CD}{b}\times\color{#EC0000}{h}}{2}| |
|
|
|\begin{align} |
|\begin{align} |
|
|
|\begin{align} |
|A=\color{#3B87CD}{b}\times\color{#EC0000}{h}| |
|
|
|\begin{align} |
|A=\color{#3B87CD}{b}\times\color{#EC0000}{h}| |
|
|
|\begin{align} |
|A=\dfrac{\color{#FF55C3}{D}\times\color{#3B87CD}{d}}{2}| |
|
|
|P=\color{#3B87CD}{b}+\color{#3A9A38}{a}+\color{#FA7921}{B}+\color{#FF55C3}{c}| |
|A=\dfrac{(\color{#3B87CD}{b}+\color{#FA7921}{B})\times\color{#EC0000}{h}}{2}| |
|
|
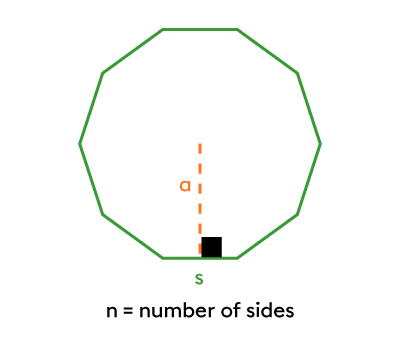
|P=n\times\color{#3A9A38}{s}| |
|A=\dfrac{\color{#3A9A38}{s}\color{#FA7921}{a}n}{2}| |
|
|
|C=2\pi\color{#3A9A38}{r}| |
|A=\pi\color{#3A9A38}{r}^2| |