A piecewise function is a function whose rule differs according to the interval where the variable |x| is located.
As the name suggests, a piecewise function is made up of several pieces – or parts.
Usually, each part is defined by its own equation over a specific interval. Thus, we obtain
| f(x)=\left\{ \begin{align} \text{equations} & && \text{domain}\\ \color{blue}{ 1^{\text{st}} \ \text{part}}&& & \color{blue}{\text{values of} \ x} \\ \color{red}{2^{\text{nd}} \ \text{part}}&& & \color{red}{\text{values of} \ x }\\ \color{green}{3^{\text{rd}} \ \text{part}}&& & \color{green}{\text{values of} \ x }\\ ... &&& ... \end{align} \right.||
Therefore, a multitude of functions can be combined to form a single one.
Here is a graph representing a piecewise function:
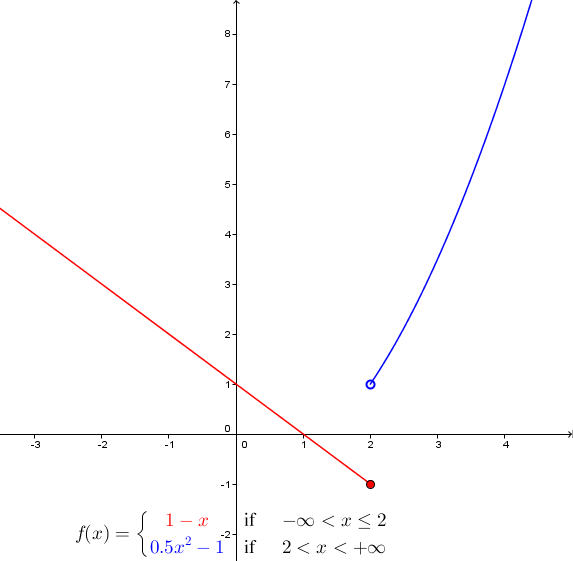
The function plotted in red exists over the interval |]-\infty,2]|. The function plotted in blue exists over the interval |]2, + \infty[|.
The basic idea behind the construction is to plot each of the given equations, then restrict them to the interval defining them.
Use the following information to plot the piecewise function:
||f(x)=\left\{ \begin{align}
&\color{purple}{ 2x + 3}& \ \text{if} && \color{purple}{0 \leq x < 4}\\
&\color{blue}{x^2-3x-1}& \ \text{if} && \color{blue}{4 \leq x < 6}\\
&\color{green}{x}& \ \text{if} && \color{green}{6 \leq x \leq 8}\end{align} \right.||
-
Draw each of the functions without considering their domain
-
Break down each of the functions according to their domain
During this step, do not forget to indicate which part of each of the functions should be kept.
-
Identify the included (full point) and excluded (empty point) values
To achieve this, refer to the inequalities present for each interval.
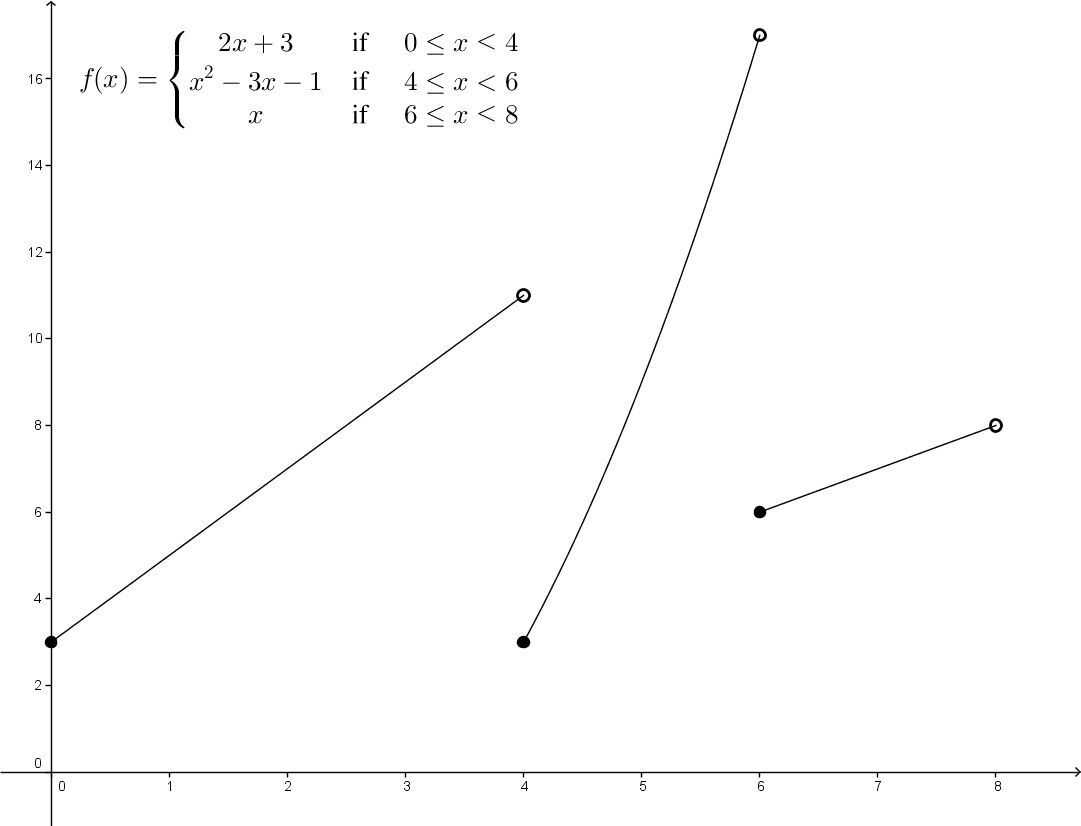
In the first parts, |0| is less than or equal to |x| (|0| is included) and |4| is taller than |x| (|4| is excluded). The same reasoning is used for the other critical points.
The following process structure can help resolve the majority of situations involving a piecewise function.
During a hot air balloon ride, the altitude above ground is illustrated according to the following function:

Since it is at the mercy of the strength and direction of the wind, it is sometimes difficult to control a hot air balloon. To avoid interfering with the flight corridors of various aircraft, a hot air balloon must not fly higher than |1 \ 200 \ m|.
How long were the hot air balloon and its occupants at a dangerous altitude?
-
Determine the equation(s) of the essential parts
Equation of |\overline{AB}| with the form |y = ax + b|:
||\begin{align} a &= \frac{y_2-y_1}{x_2-x_1} \\ &= \frac{1272 - 864}{14-8} \\
&= 68 \end{align}|| ||\begin{align}
y &= 68x + b \\ \Rightarrow 1272 &= 68 (14) + b \\
1272 &= 952 + b \\
320 &=b \end{align}||
Thus, the equation of |\overline{AB}| is | y = 68x + 320|.Equation of |\overline{CD}| with the form |y = ax + b|:
||\begin{align}
a &= \frac{y_2-y_1}{x_2-x_1} \\ &= \frac{1314- 0}{28-64} \\
&= -36.5\\
\end{align}|| ||\begin{align} y &= -36.5x+ b \\ \Rightarrow 0 &= -36.5 (64) + b \\
0 &= -2 \ 336 + b \\
2\ 336 &= b \end{align}||
Thus, the equation of |\overline{CD}| is | y = -36.5x + 2 \ 336|. -
Solve the equation(s) according to the context
Since we are interested in the time |x| when the altitude |y| was |1 \ 200 \ m|, we obtain:According to |\overline{AB}| : ||\begin{align} y &= 68x + 320 \\
\Rightarrow 1 \ 200 &= 68x + 320 \\
880 &= 68 x \\
12.94 &\approx x \end{align}||According to |\overline{CD}| : ||\begin{align} y &= -36.5x + 2 \ 336 \\
\Rightarrow 1 \ 200 &= -36.5x + 2 \ 336 \\
-1 \ 136 &= -36.5x \\
31.12 &\approx x \end{align}|| -
Formulate an adequate answer
The hot air balloon was at a dangerous altitude for about |31{.}12 - 12{.}94 = 18{.}18| min.
Pour valider ta compréhension à propos de la résolution graphique de fonctions définies par parties, périodiques et en escalier de façon interactive, consulte la MiniRécup suivante.
