La fonction définie par parties

Une fonction définie par parties est une fonction dont la règle diffère selon l'intervalle où se situe la variable |x|.

Généralement, chacune des parties est définie par une équation qui lui est propre sur un intervalle précis. Ainsi, on obtient
|| f(x)=\left\{ \begin{align} \text{équations} & && \text{domaine}\\ \color{blue}{ 1^{\text{re}} \ \text{partie}}&& & \color{blue}{\text{valeurs de} \ x} \\ \color{red}{2^{\text{e}} \ \text{partie}}&& & \color{red}{\text{valeurs de} \ x }\\ \color{green}{3^{\text{e}} \ \text{partie}}&& & \color{green}{\text{valeurs de} \ x }\\ ... &&& ... \end{align} \right.||

Voici un graphique représentant une fonction définie par parties :

La fonction tracée en rouge est celle qui vit sur l'intervalle |]-\infty,2]|. La fonction tracée en bleue est celle qui vit sur l'intervalle |]2, + \infty[|.

Utilise les informations suivantes pour tracer la fonction définie par parties :
||f(x)=\left\{ \begin{align}
&\color{purple}{ 2x + 3}& \ \text{si} && \color{purple}{0 \leq x < 4} \\
&\color{blue}{x^2-3x-1}& \ \text{si}  && \color{blue}{4 \leq x < 6}\\
&\color{green}{x}& \ \text{si}  && \color{green}{6 \leq x \leq 8}\end{align} \right.||

1. Tracer chacune des fonctions sans tenir compte de leur domaine

2. Découper chacune des fonctions selon leur domaine

Lors de cette étape, ne pas oublier d'indiquer quelle partie de chacune des fonctions doit être conservée.

3. Identifier les valeur incluses (point plein) et exclues (point vide)

Pour y arriver, on doit se référer aux inéquations présentes dans chacune des intervalles.

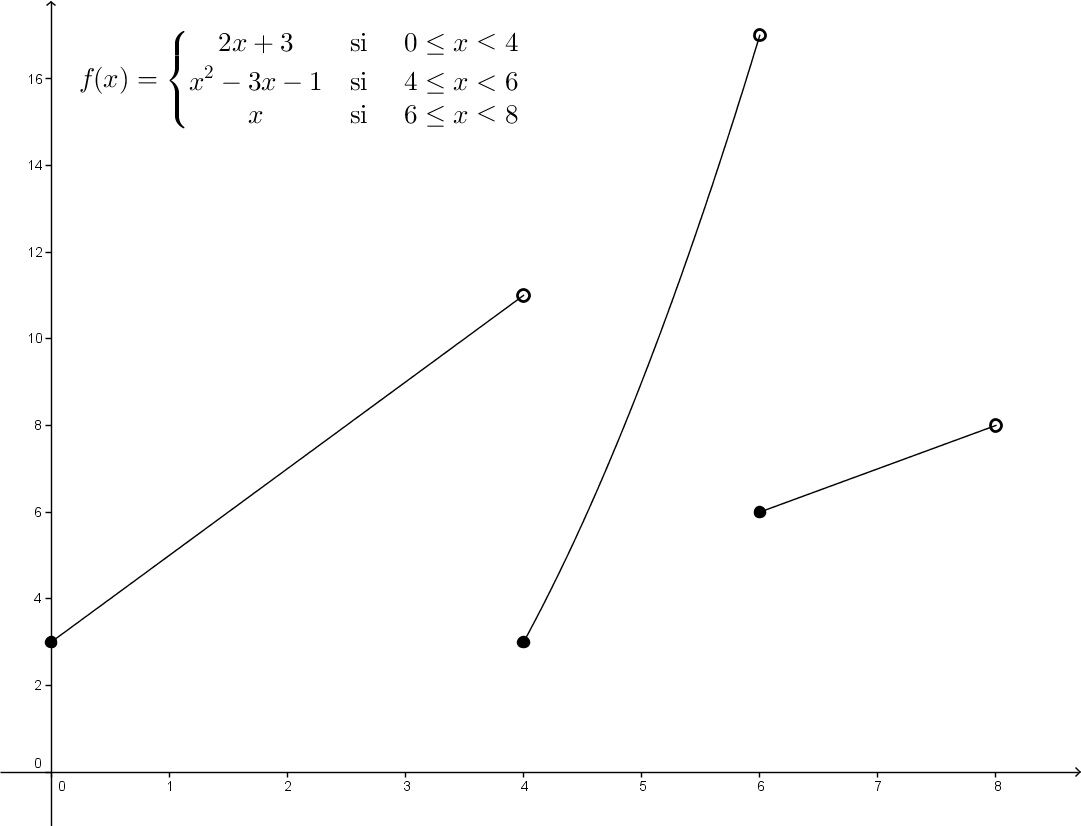
Dans le cas de la première parties, |0| est plus petit ou égal à |x| (|0| est inclus) et |4| est plus grand que |x| (|4| est exclu). On utiliser le même genre de raisonnement pour les autres points critiques.
 

Lors d'un tour en montgolfière, l'altitude par rapport au sol est modélisé selon la fonction suivante :

Étant à la merci de la force et de la direction du vent, il est parfois difficile de contrôler une montgolfière. Afin de ne pas interférer avec les corridors de vol des différents aéronefs, une montgolfière ne doit pas voler à plus de |1 \ 200 \ m| d'altitude.
Pendant combien de temps la montgolfière et ses voyageurs étaient-ils à une altitude à risque?

1. Déterminer la ou les équations des parties essentielles
   
   Équation de |\overline{AB}| sous la forme |y = ax + b:| ||\begin{align} a &= \dfrac{y_2-y_1}{x_2-x_1} \\ &= \dfrac{1\ 272 - 864}{14-8} \\ &= 68 \end{align}|| ||\begin{align} y &= 68x + b \\ \Rightarrow 1\ 272 &=  68(14) + b \\ 1\ 272 &= 952 + b \\ 320 &=b \end{align}||Ainsi, l'équation de |\overline{AB}| est | y = 68x + 320.|
   
   Équation de |\overline{CD}| sous la forme |y = ax + b:| ||\begin{align} a &= \dfrac{y_2-y_1}{x_2-x_1} \\ &= \dfrac{1\ 314- 0}{28-64} \\ &=  -36{,}5\\ \end{align}|| ||\begin{align} y &= -36{,}5x+ b \\ \Rightarrow 0 &= -36{,}5 (64) + b \\ 0 &= -2\ 336 + b \\ 2\ 336 &= b \end{align}||Ainsi, l'équation de |\overline{CD}| est | y = -36{,}5x + 2\ 336.|

2. Résoudre la ou les équations selon le contexte
   
   Puisqu'on s'intéresse au temps |x| quand l'altitude |y| était de |1\ 200\ \text{m},| on obtient :
   
   Selon |\overline{AB}:| ||\begin{align} y &=  68x + 320 \\ \Rightarrow 1 \ 200 &=  68x + 320 \\ 880 &= 68 x \\ 12{,}94 &\approx x \end{align}||Selon |\overline{CD}:| ||\begin{align} y &= -36{,}5x + 2\ 336 \\ \Rightarrow 1\ 200 &=  -36{,}5x + 2 \ 336 \\ -1\ 136 &= -36{,}5x \\ 31{,}12 &\approx  x \end{align}||

3. Formuler une réponse adéquate
   
   Au final, la montgolfière se trouvait à une altitude à risque pendant environ |31{,}12 - 12{,}94 = 18{,}18| min.