Adding the parameters |a,| |b,| |h|, and |k| to the base function |f(x)=[x]| results in what is called the standard form (or transformed form) of the step function.
The standard form of the step function is: ||f(x)=a[b(x-h)]+k|| where |a,| |b,| |h,| and |k| are real numbers that function as parameters.
Note: The parameters |a| and |b| are always non-zero.
In the following interactive animation, experiment with the parameters |a|, |b|, |h,| and |k| of the step function. Observe the changes that take place on the transformed curve (in green) compared to the basic function (in black). Try to analyze the function’s properties. Afterwards, look at the concept sheet for information about each of the parameters.
When |{\mid}a{\mid} >1|:
The larger the absolute value of the parameter |a|, the greater the distance between the steps. The function curve stretches vertically compared to the basic function.

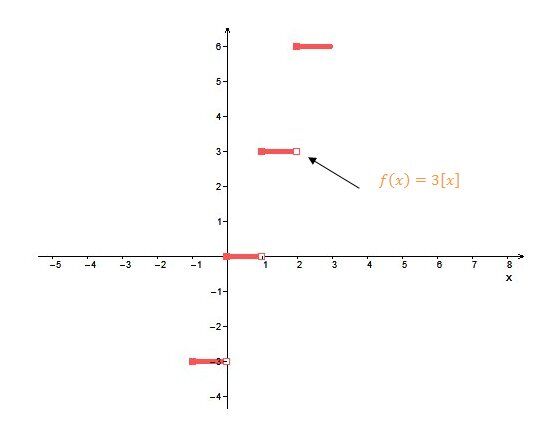
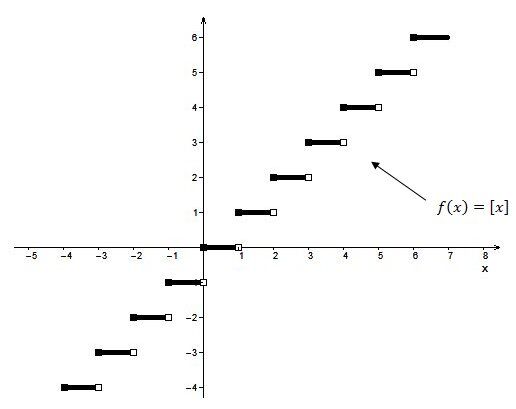
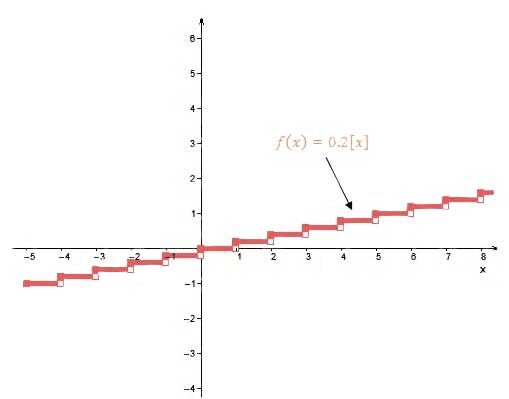
When |0< {\mid}a{\mid} <1|:
The smaller (closer to |0|) the absolute value of the parameter |a|, the shorter the distance between the steps. The function approaches the |x|-axis.
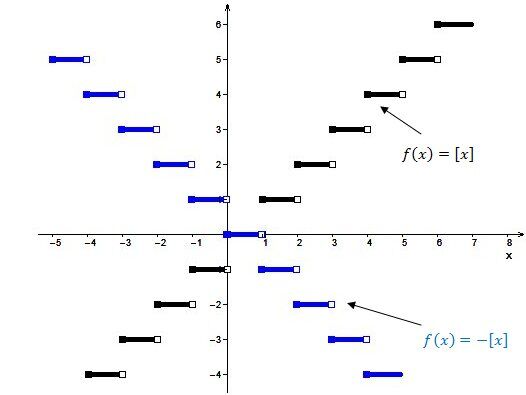
Reflection across the |x|-axis
The parameter |a| is also responsible for the orientation of the step function.
When |a| changes sign, the step function is reflected across the |x|-axis.
When |{\mid}b{\mid} >1|:
If the absolute value of |b| increases, then the length of the steps becomes smaller. The steps shorten horizontally relative to the base function.
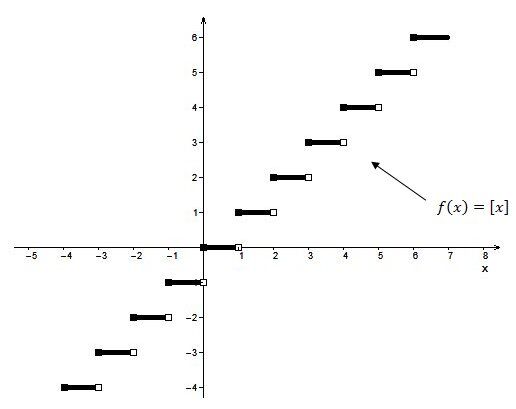
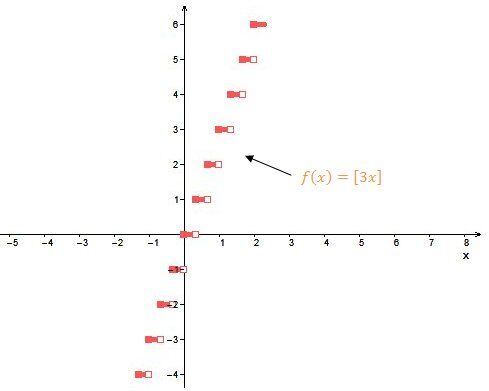
When |0< {\mid}b{\mid} <1|:
The length of the segments extends by a factor of |\dfrac{1}{b}| compared to the base function. The steps lengthen horizontally. The smaller (closer to |0|) the absolute value of |b|, the greater the length of the steps.
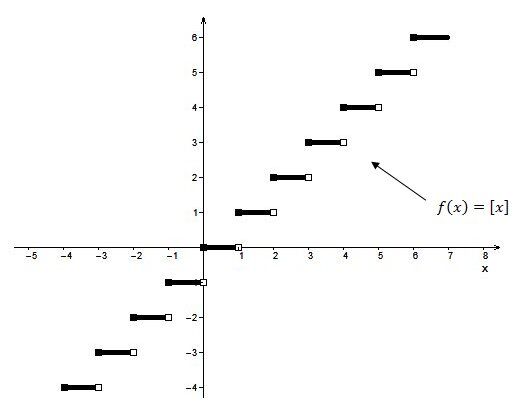
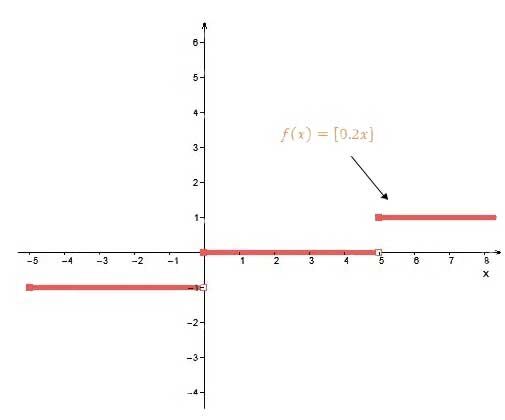
The parameter |b| is also responsible for the orientation of the step function. When |b| changes sign, the steps are reflected across the |y|-axis.
When |b| is positive |(b>0)|:
Each segment has a closed point on the left and an open point on the right.
When |b| is negative |(b<0)|:
Each segment has an open point on the left and a closed point on the right.

When |h| is positive |(h>0)|:
The steps move to the right.
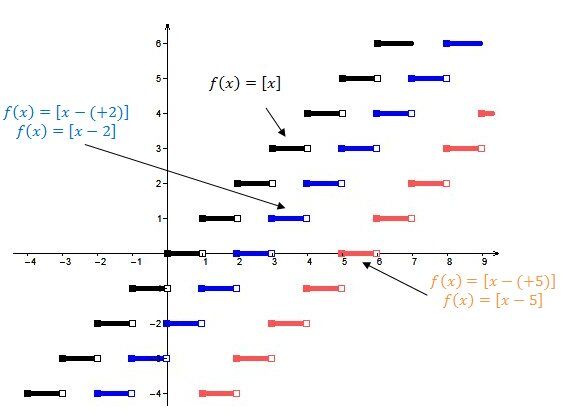
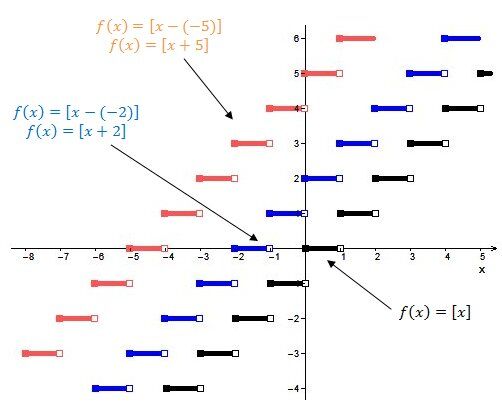
When |h| is negative |(h<0)|:
The steps move to the left.
When |k| is positive |(k>0)|:
The steps shift vertically upwards.
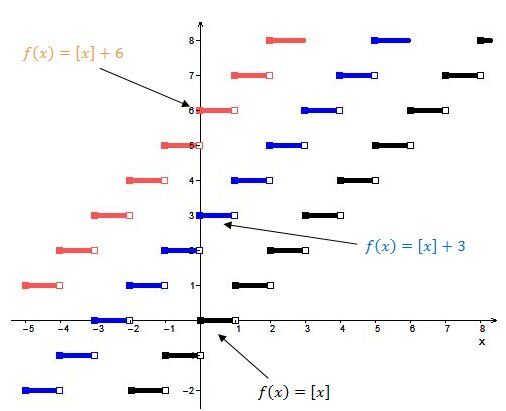
When |k| is negative |(k<0)|:
The steps shift vertically downwards.
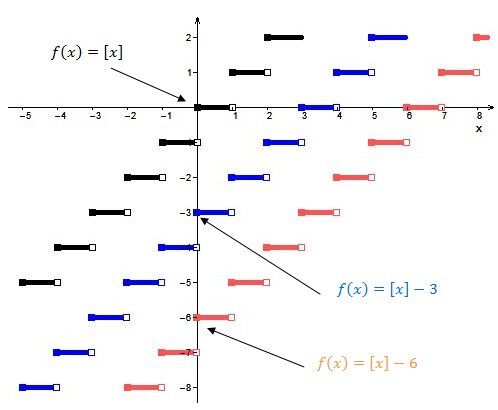
It is useful to note that we can determine if a step function is increasing or decreasing as follows.
“Slope” of the steps |= a b|
-
If |ab| is positive, the function is increasing.
-
If |ab| is negative, the function is decreasing.