After adding in the parameters |a,| |b,| |h,| and |k| to the base function|f(x)=\tan(x),| the resulting function is said to be written in the standard form (also called the transformed form) of the tangent function.
The standard form of a tangent function is:
||f(x)=a \tan(b(x-h))+k||
where |a,| |b,| |h| and |k| are real numbers that act as parameters.
Note: The parameters |a| and |b | are never zero.
In the following animation, experiment with the parameters |a| , |b| , |h|, and |k| of the tangent function. Notice the changes that take place on the transformed curve (in black) relative to the base function (in orange). Observe the effect that manipulating the parameters has on the function’s properties. After experimenting, continue to read this concept sheet for information on each parameter.
When |{\mid}a{\mid} >1:|
As the absolute value of |a| gets larger, the function’s inflection points get further away from the horizontal axis and the function stretches vertically.
When |0< {\mid}a{\mid} <1:|
As the absolute value of |a| approaches 0, the function’s inflection points approach the horizontal axis. The function becomes less vertical.
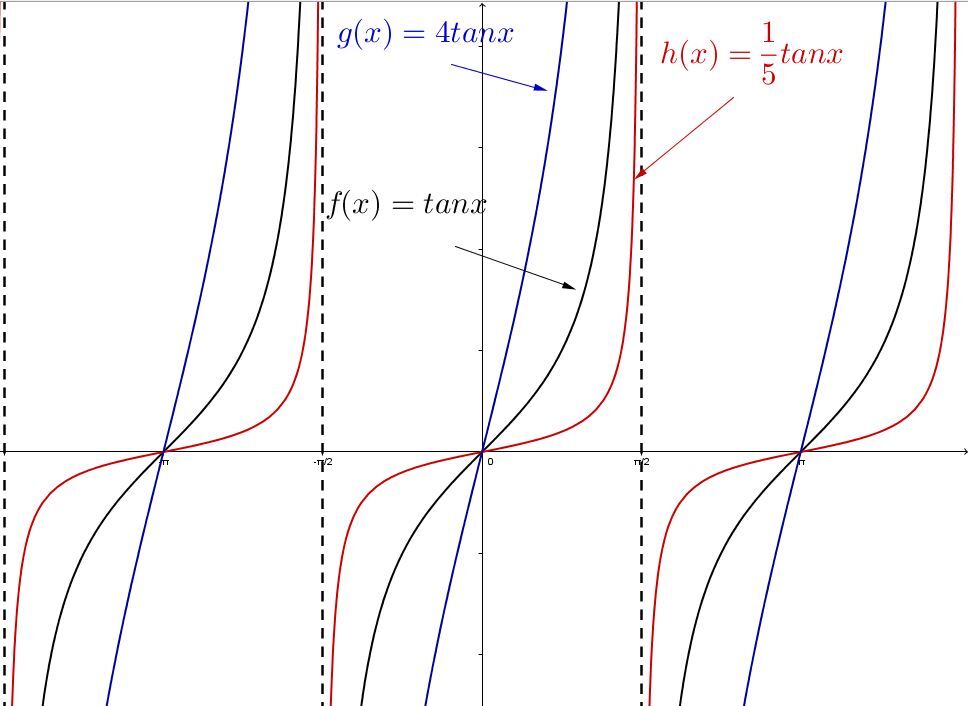
The parameter |a| is responsible for the orientation of the graph of the tangent function.
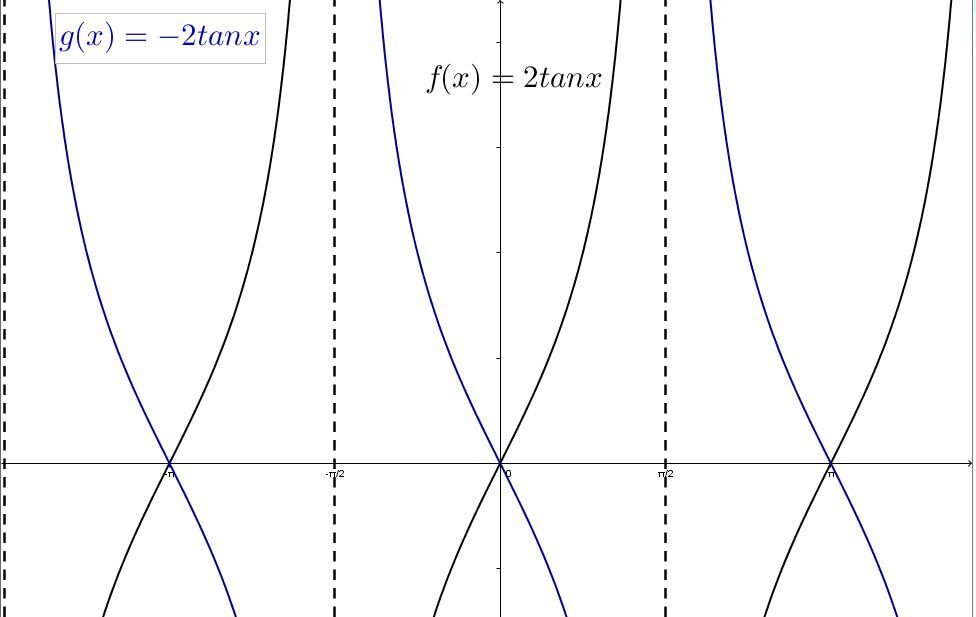
When |a| is negative |(a<0):|
The function is reflected across the |x|-axis.
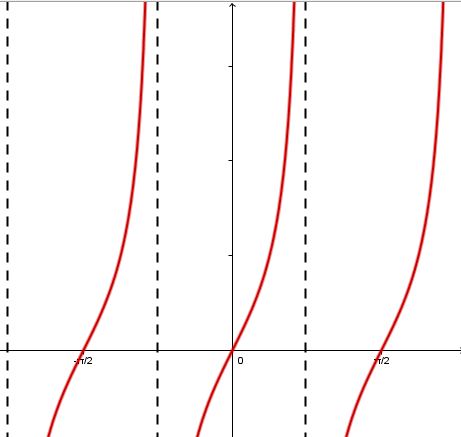
When |{\mid}b{\mid} >1:|
As the absolute value of |b| becomes larger, the period becomes smaller. The distance between two zeroes in the function also becomes smaller.
When |0< {\mid}b{\mid} <1:|
As the absolute value of |b| gets smaller (closer to 0), the period becomes larger. The distance between two zeroes of the function thus becomes larger.
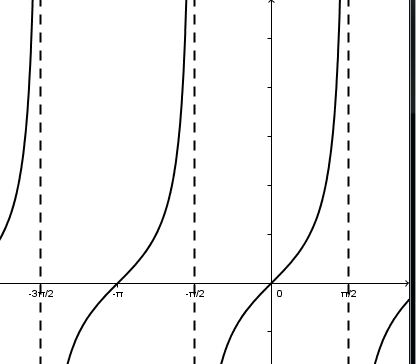
| |g(x)=\tan(2x)| |P=\dfrac{\pi}{2}| |
|f(x)=\tan(x)| |P=\pi| |
|h(x)=\tan(\frac{1}{2}x)| |P=2\pi| |
|---|---|---|
 |
 |
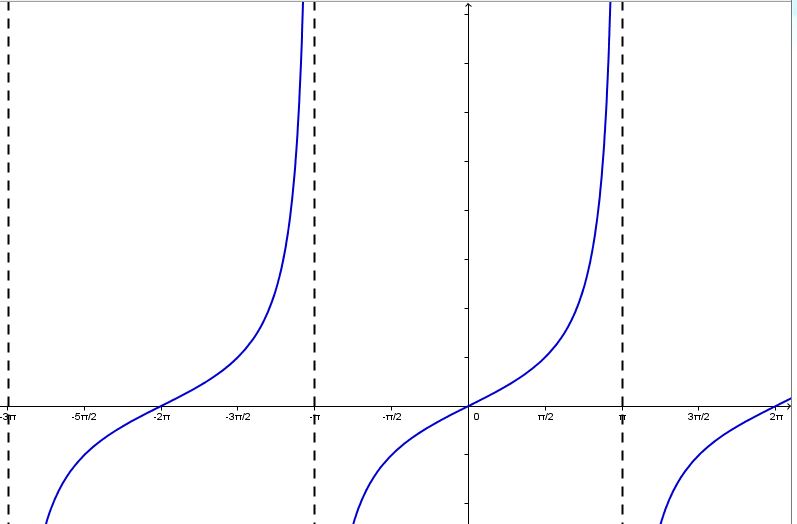 |
The parameter |b| is also responsible for the orientation of the graph of the tangent function.
When |b| is negative |(b<0):|
The function is reflected across the |y|-axis.

Since the curve of a tangent function can be reflected, the sign of the parameters |a| and |b| predicts whether the function increases or decreases between two asymptotes.
When |a| and |b| have the same sign |(ab>0):|
The function increases between two asymptotes.
When |a| and |b| have opposite signs |(ab<0):|
The function decreases between two asymptotes.
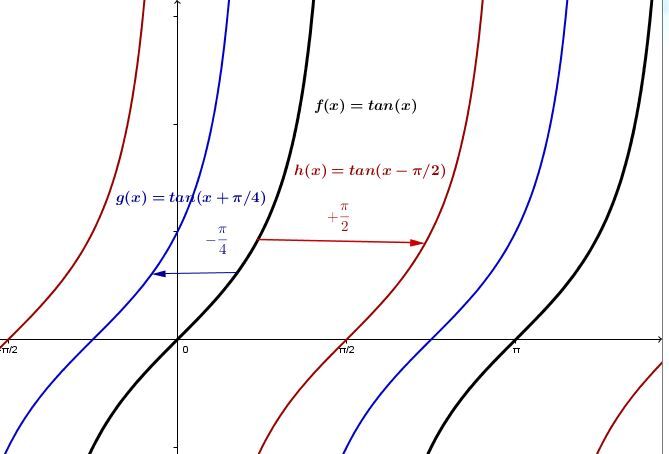
The parameter |h| is responsible for the horizontal displacement of the curve. This is also called the phase shift of a periodic function.
When |h| is positive |(h>0):|
The curve of the tangent function moves to the right.
When |h| is negative |(h<0):|
The curve of the tangent function moves to the left.
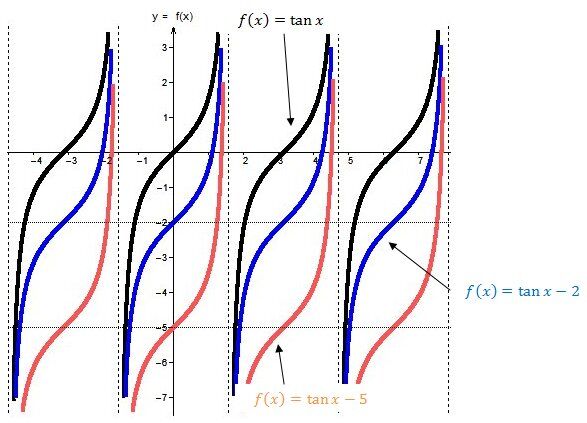
When |k| is positive |(k>0):|
The curve of the tangent function moves upwards.

When |k| is negative |(k<0):|
The curve of the tangent function moves downward.