When we consider the value of the slope of the line connecting the centre of the unit circle to a precise point on that circle, the tangent function is used.
In other words, |\tan(\theta)=\dfrac{\Delta y}{\Delta x}=\dfrac{\sin(\theta)}{\cos(\theta)}| where |\theta| is the measurement of the central angle of the trigonometric circle.
-
The dotted lines correspond to the asymptotes of the basic tangent function. The equations of the asymptotes in red are |x=-\dfrac{\pi}{2}| and |x=\dfrac{\pi}{2}.|
-
The period of the basic tangent function is |\pi| radians.
-
The point |(0,0)| is the inflection point of the function.
The tangent function in standard form is written as: ||f(x)=a \tan\big(b(x-h)\big)+k||
where
||\begin{align}\vert b\vert&=\dfrac{\pi}{\text{Period}}\\h&:\text{Function’s horizontal phase shift}\\k&:\text{Function’s vertical translation}\end{align}||
Notes:
The point |(h,k)| corresponds to the inflection point of the function.
The parameters |a| and |b| are not equal to |0.|
The Period
The period is the distance between two consecutive asymptotes.
The period of the function is found from the following formula: ||P= \dfrac{\pi}{\mid b \mid}||
Thus, the value of |b| can be found by isolating it in the formula, resulting in: ||{\mid}b{\mid} = \dfrac{\pi}{P}||
Next, the sign of |b| is adjusted depending on the variation of the curve.
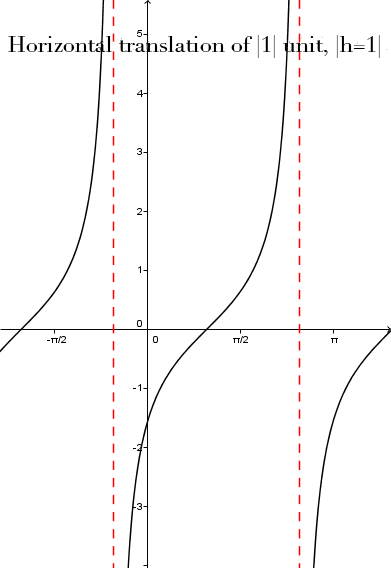
The Phase Shift
The phase shift is the horizontal translation from the point of origin |(0,0)| of the basic function. It is denoted by the letter |h| in the tangent function equation’s standard form. Asymptotes also move by |h| units.
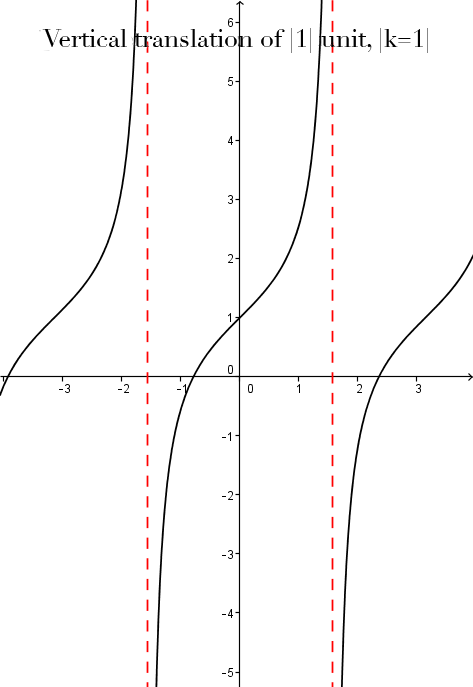
Parameter |k|
The parameter |k| corresponds to the vertical translation from the point of origin |(0,0)| of the basic function.
The asymptotes of a tangent function
The asymptotes of the tangent function are vertical lines. Since the tangent function is a periodic function, the cycle (pattern) repeats indefinitely. Therefore, there are an infinite number of asymptotes which are defined by an equation of the form: |x=\left(h+\dfrac{P}{2}\right)+nP|, where |n\in\mathbb{Z}| and |P| is the period of the function. The distance between the asymptotes is |P.|
