The slope (rate of change) of a segment or a line, generally denoted by the variable |m,| corresponds to the value of its incline with respect to the |x|-axis.
The slope of a line corresponds to the ratio of the difference of the |y|-coordinates and the difference of the |x|-coordinates of two points on the line.
When the two points |A(x_1,y_1)| and |B(x_2,y_2)| are given, the slope can be calculated using the following formula.
|slope=m=\displaystyle \frac{\Delta y}{\Delta x}=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}}|
Calculate the slope of the following segment.
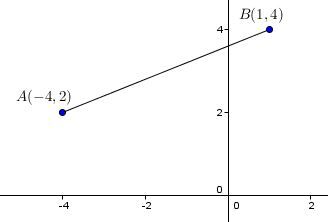
|slope=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}}|
|slope=\displaystyle \frac{4-2}{1-(-4)}|
|slope=\displaystyle \frac{2}{5}|
The rate of change (slope) is therefore 2/5. This means that every time 5 units are moved on the positive |x|-axis, 2 units are moved up on the |y|-axis.

Four different inclines can be found depending on the type of slope that is observed.
-
An increasing line has a positive slope.
-
A decreasing line has a negative slope.
-
A horizontal line has a slope of zero.
-
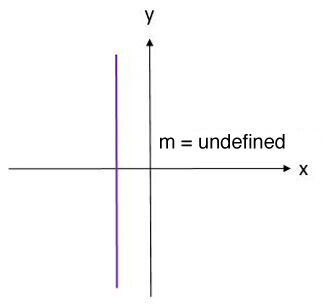
A vertical line has an undefined slope.

With a horizontal segment, the slope is |0,| because the numerator is equal to zero ( |y_2 – y_1 = 0| ).
With a vertical segment, the slope is undefined, because the denominator in the slope calculation is zero ( |x_2 – x_1 = 0| ). The result of a division by |0| is undefined.
It is possible to determine the slope of a line from the parameters of the equation when the latter is given.
|
|
General form |Ax + By + C = 0| |
Functional form |y = mx + b| |
Symmetric form |\dfrac{x}{a} + \dfrac{y}{b} = 1| |
|
Slope |
|\dfrac{-A}{B}| |
|m| |
|\dfrac{-b}{a}| |
In a relation between two variables represented by a linear function, the slope is defined as the rate of change.