La pente d’un segment ou d'une droite, généralement symbolisée par la variable |m,| correspond à la valeur de son inclinaison par rapport à l'axe des abscisses.
La pente d'une droite correspond au rapport de la différence des ordonnées et de la différence des abscisses entre deux points de cette droite.
Lorsqu'on connait deux points |A(x_1,y_1)| et |B(x_2,y_2),| il est possible de calculer la pente à l'aide de la formule suivante :
|pente=m=\displaystyle \frac{\Delta y}{\Delta x}=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}}|
Calculer la pente du segment suivant :
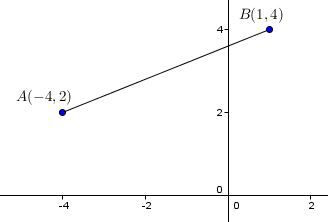
|pente=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}}|
|pente=\displaystyle \frac{4-2}{1-(-4)}|
|pente=\displaystyle \frac{2}{5}|
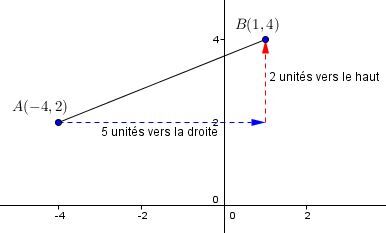
Le taux de variation est donc de 2/5. Cela signifie qu’à chaque fois que l’on se déplace de 5 unités sur l’axe des x positif, on monte de 2 unités sur l’axe des y.
On peut retrouver 4 inclinaisons différentes selon le type de pente que l'on observe.
-
Une droite ascendante a une pente positive.
-
Une droite descendante a une pente négative.
-
Une droite horizontale a une pente nulle.
-
Une droite verticale a une pente indéterminée.

Dans le cas d’un segment horizontal, la pente est de 0, car le numérateur est égal à zéro (|y_2 – y_1 = 0|).
Dans le cas d’un segment vertical, la pente est indéfinie, car le dénominateur dans le calcul de la pente est égal à zéro (|x_2 – x_1 = 0|). Le résultat d'une division par 0 est indéfini.
Il est possible de déterminer la pente d'une droite à partir des paramètres de l'équation, lorsque celle-ci est donnée.
|
|
Forme générale |Ax + By + C = 0| |
Forme fonctionnelle |y = mx + b| |
Forme symétrique |\dfrac{x}{a} + \dfrac{y}{b} = 1| |
|
Pente |
|\dfrac{-A}{B}| |
|m| |
|\dfrac{-b}{a}| |
Dans une relation entre deux variables représentée par une fonction afine, on définit la pente comme étant un taux de variation :