Mathematical equations and inequalities are not always given in a word problem. To solve such a situation, it is first necessary to translate the written statements using one or more equations, or one or more inequalities. We can then find the solution(s) to the problem by solving the equations or inequalities.
Going from a word problem to a mathematical equation is like translating from one language to another. In fact, the term “translate" is used when asked to change a written statement into a mathematical equation.
The following steps must be taken to translate a written statement into an equation:
-
Carefully read the word problem and identify the given data and variables.
-
Identify the relationship between the variables.
-
Translate this relationship into an equation or an algebraic expression.
When translating a written statement into an equation, certain keywords give clues about which operations to perform.
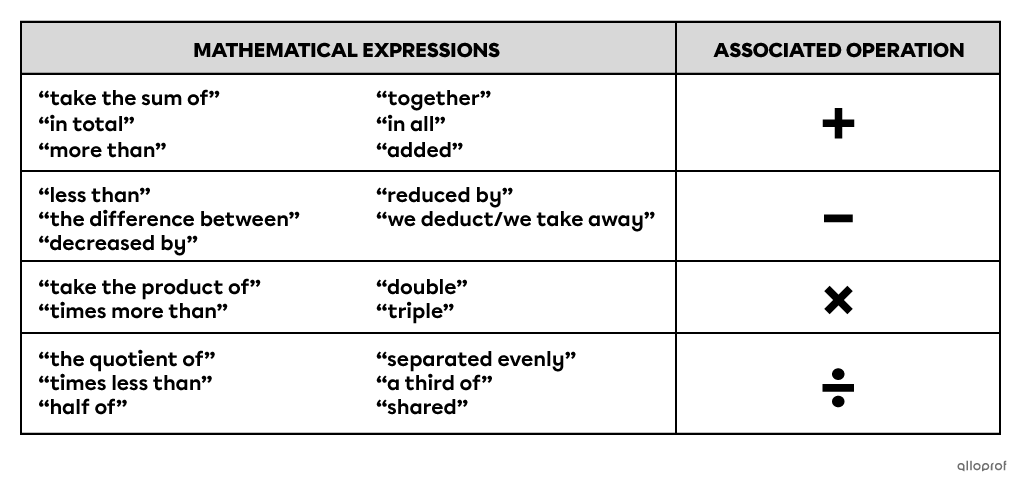
Only the most common expressions are written in this table. For a more comprehensive list of each operation (i.e., adding, subtracting, multiplying and dividing), the virtual library’s concept sheets for such operations are a good resource.
Some problem statements produce relationships amongst data. In this case, you need to establish the algebraic expressions for each variable before writing an equation.
Translation of Statements Into Algebraic Expressions
-
If it reads "three times as many cats as dogs," we can write the following equation:
Cats = |3| times dogs
The relationship between the number of cats and dogs will be as follows:
If |n| is the number of dogs, the number of cats is |3n.|
|\text{Number of dogs} = n|
|\text{Number of cats} = 3n| -
If it reads “three times fewer dogs than cats,” we can write the following equation:
Dogs = |\dfrac{1}{3}| times cats
The relationship between the number of dogs and cats will be the following:
If |m| is the number of cats, the number of dogs is |\dfrac{m}{3}| or |\dfrac{1}{3}\times m.|
|\text{Number of dogs} = \dfrac{m}{3}|
|\text{Number of cats} = m| -
If it reads “Luke is four years older than Kim,” we can write the following equation:
|\text{Luke's age} = \text{Kim's age} + 4|
The relationship between Luke's age and Kim's age will be the following:
If |x| is Kim's age, Luke's age is |x + 4.|
|\text{Kim’s age} = x|
|\text{Luke’s age} = x + 4| -
If it reads “Kim is four years younger than Luke,” we can write the following equation:
|\text{Kim's age} = \text{Luke's age} - 4|
The relationship between Kim's age and Luke's age will be the following:
If |y| is Luke's age, Kim's age is |y – 4.|
|\text{Luke’s age} = y|
|\text{Kim’s age} = y - 4|
After determining the mathematical expression of the variables, the problem can be translated into an equation.
Martine mows lawns to collect pocket money. She charges |\$5| to mow one lawn. What equation can be used to translate the situation?
-
We identify and declare the variables (which can vary in the problem):
Variable 1: Number of lawns mowed by Martine (|x|).
Variable 2: Money raised by Martine according to the number of lawns mowed (|y|). -
We identify the relationship between the variables.
Martine receives |$5| for each lawn she mows.
We can also say that the more lawns she mows, the more the sum earned increases. -
We translate the relationship into an equation:
The money earned by Martine = |\$5| multiplied by the number of lawns mowed
|y = 5x|
In two years, Charles will be half the age Danny is now. What equation can be used to translate the situation?
-
Identify the variables (which can vary in the problem):
Variable 1: Charles' age at the moment |(x)|.
Variable 2: Danny's age at the moment |(y)|. -
Identify the relationship between the variables:
In two years, Charles will be half the age Danny is now.
We can also say Charles’ current age plus |2| years will be equal to half of Danny’s current age plus |2| years. -
Translate the relationship into an equation:
Charles' age in |2| years = |\dfrac{1}{2}| of Danny's age in |2| years.||x+2=\dfrac{1}{2}(y+2)||
To confirm your understanding about solving algebraic problems, see the following interactive Crash Lesson:

Be careful: some statements will not translate into an equation. Instead, they will translate into an inequality.
Going from a word problem to a mathematical inequality is like translating from one language to another. In fact, the term “translate" is used when asked to change a written statement into a mathematical inequality.
The following steps must be taken to translate a statement into an equality:
-
Carefully read the written problem and identify the known data and variables.
-
Identify the relationship between the variables.
-
Translate the relationship into an inequality or an algebraic expression.
When translating a written statement into an inequality, pay attention to certain keywords which provide clues about which inequality symbol to use.
-
There are more than |5| people. |\to\ x > 5|
-
The sum of two numbers is less than |36.| |\to\ x + y < 36|
-
There are at least |150| spectators. |\to\ x \ge 150|
-
He cannot work more than |40| hours per week. |\to\ x \le 40|