Multiplication is an operation that makes it possible to repeat a number or a quantity a certain number of times.
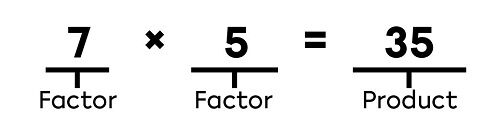
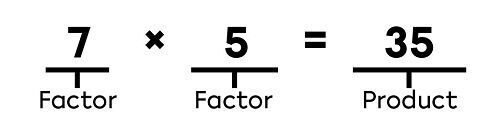
In multiplication, the multiplied numbers are called factors. The result of a multiplication is called the product.
To find out what the × and = symbols mean, you can read the concept sheet Glossary of Mathematical Symbols (coming soon).
To find the product, a multiplication can be represented as a series of repeated additions using a picture or objects. For example, tokens or cubes can be used to help with the calculations.
The multiplication statement 5 × 7 means adding a group of 7 five times.

5 × 7 = 35
The multiplication statement 4 × 244 means adding a group of 244 four times.

244 + 244 + 244 + 244 = 976
4 × 244 = 976
-
I write the numbers one below the other, aligning the digits according to their place value. The smaller number should be written at the bottom.
-
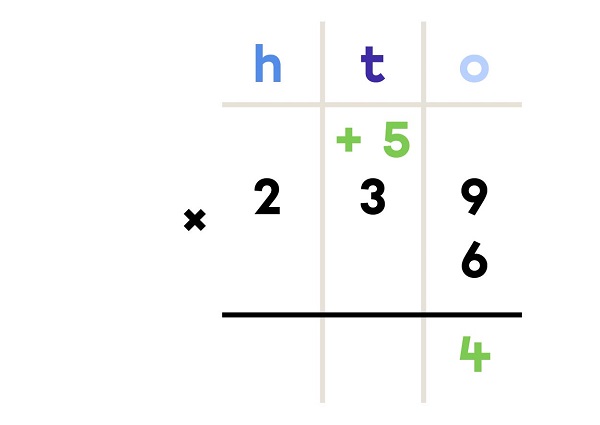
I multiply the bottom number by the digit in the ones position of the top number. If there are tens in the result, “regroup” them above the number in the tens position of the top number.
-
I repeat step 2 for all digits. Do not forget to add the regrouped number (if present).
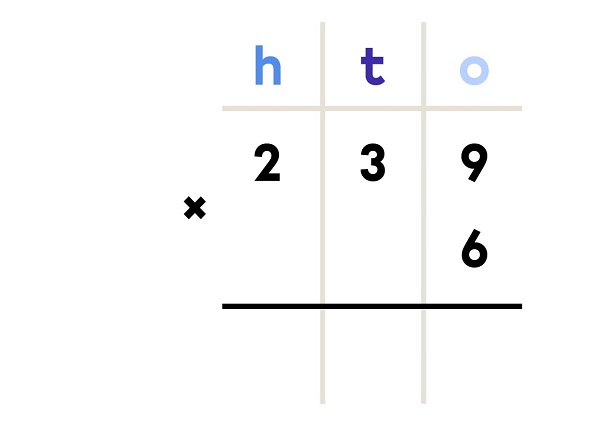
6 × 239 = ?
|
|
|
|
|
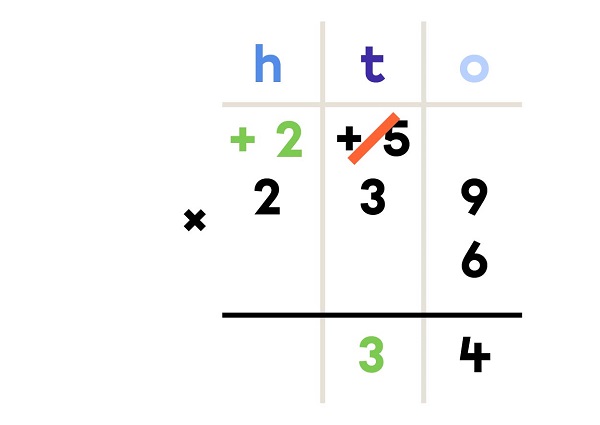 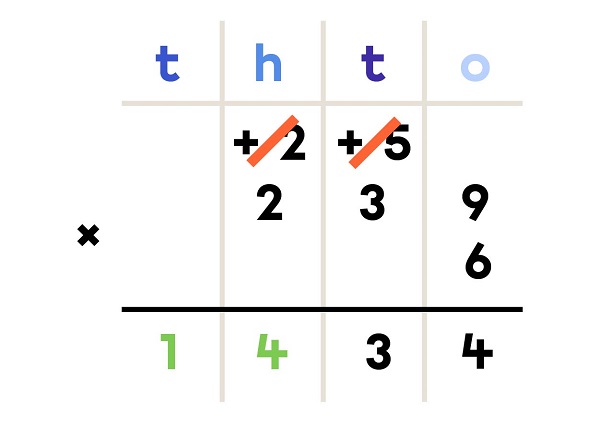 |
6 × 239 = 1 434
Multiplication is an operation that makes it possible to repeat a number or a quantity a certain number of times.
In multiplication, the multiplied numbers are called factors. The result of a multiplication is called the product.
To find out what the × and = symbols mean, you can read the concept sheet Glossary of Mathematical Symbols (coming soon).
To find the product, a multiplication can be represented as a series of repeated additions using a picture or objects. For example, tokens or cubes can be used to help with the calculations.
The multiplication statement 5 × 7 means adding a group of 7 five times.
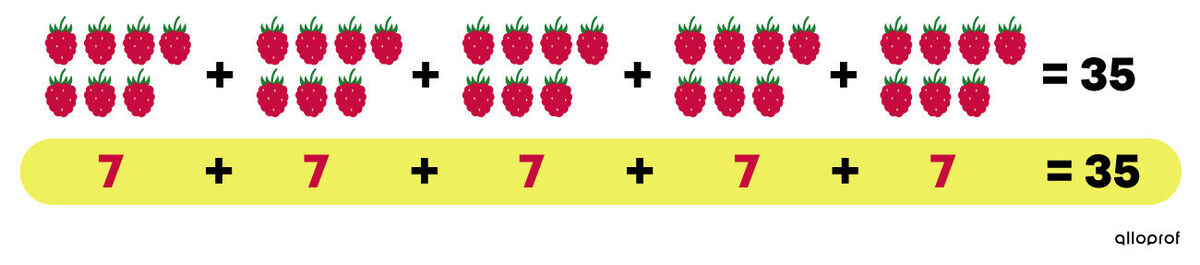
5 × 7 = 35
The multiplication statement 4 × 244 means adding a group of 244 four times.
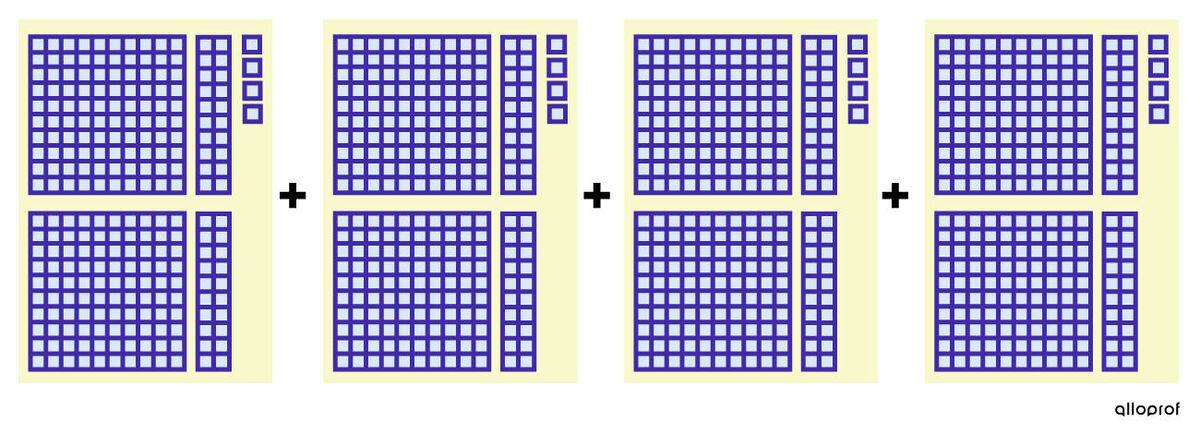
244 + 244 + 244 + 244 = 976
4 × 244 = 976
-
I write the numbers one below the other, aligning the digits according to their place value. The smaller number should be written at the bottom.
-
I multiply the bottom number by the digit in the ones position of the top number. If there are tens in the result, “regroup” them above the number in the tens position of the top number.
-
I repeat step 2 for all digits. Do not forget to add the regrouped number (if present).
6 × 239 = ?
|
 |
|
 |
|
  |
6 × 239 = 1 434
Multiplication is an operation that makes it possible to repeat a number or a quantity of objects several times.
In multiplication, the multiplied numbers are factors. The result of a multiplication is called the product.

- I write the numbers one below the other, aligning the digits according to their place value. The smaller number should be written at the bottom.
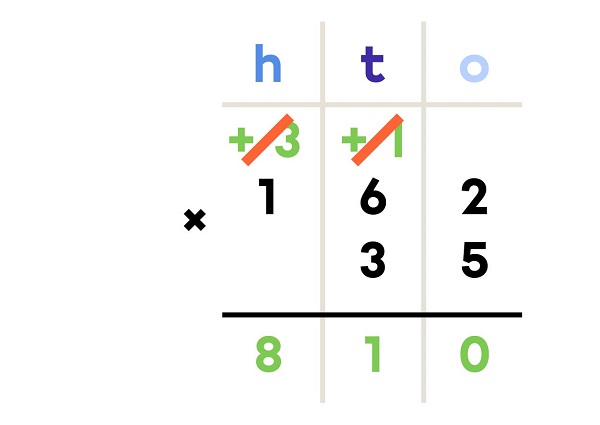
- I multiply the digit in the ones position of the bottom number by each of the digits in the top number.
- I write 0 in the ones place under the result.
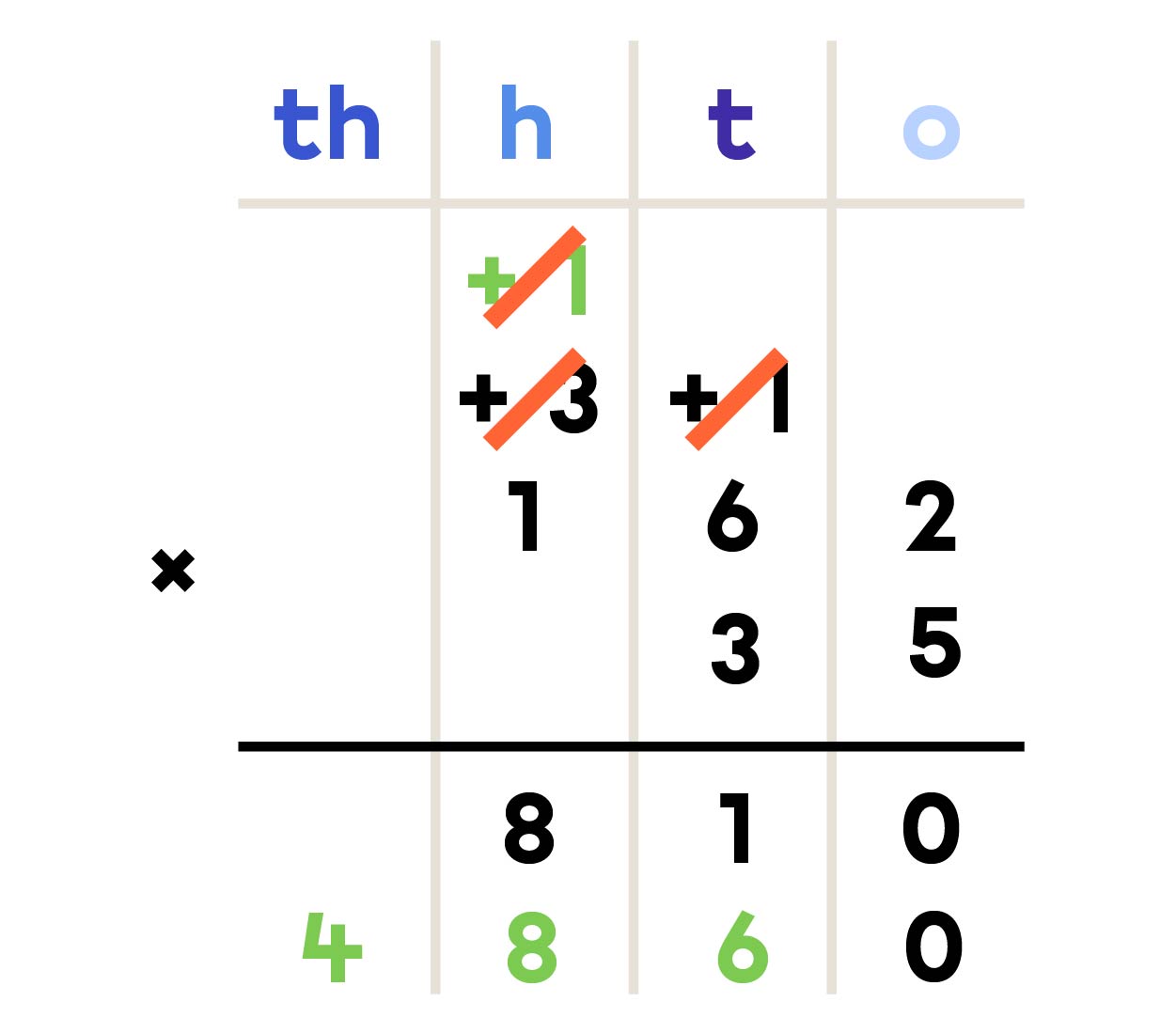
- I multiply the number in the tens position of the bottom number by each of the digits in the top number.
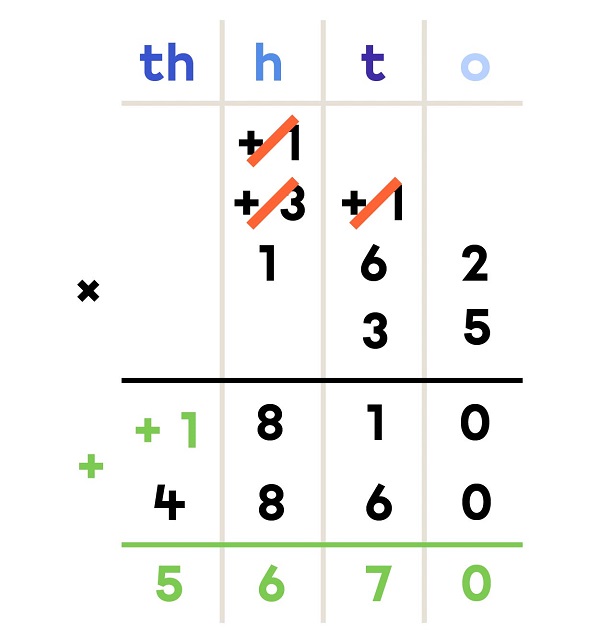
- I add the 2 results written below the line to get the final product.
35 × 162 = ?
|

|
|
|
|

|
|
|
|
|
162 × 35 = 5 670
Multiplication is an operation that makes it possible to repeat a number or a quantity of objects several times.
In multiplication, the multiplied numbers are factors. The result of a multiplication is called the product.
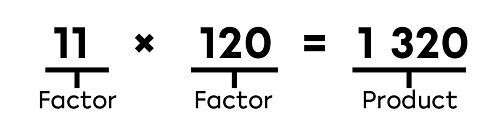
-
I write the numbers one below the other, aligning the digits according to their place value. The smaller number should be written at the bottom.
-
I multiply the digit in the ones position of the bottom number by each of the digits in the top number.
-
I write 0 in the ones place under the result.
-
I multiply the number in the tens position of the bottom number by each of the digits in the top number.
-
I add the 2 results written below the line to get the final product.
35 × 162 = ?
|
 |
|
 |
|
 |
|
 |
|
 |
162 × 35 = 5 670