A translation is a geometric transformation that associates an initial figure with an image figure through three characteristics: direction, sense, and length.
The translation of a figure consists of sliding it according to a translation arrow. This geometric transformation is an isometry.
A translation is represented by |t|. The horizontal shift which the initial figure undergoes is indicated by |a| and the vertical shift is indicated by |b|.
The transformation rule is |t_{(a,b)}:(x,y) \mapsto (x+a,y+b)|.
To translate an initial figure, apply the transformation rule to each vertex.
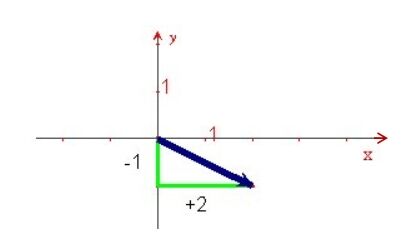
The rule is |t_{(2,-1)}: (x , y) \mapsto (x + 2 , y – 1)|.
First, we must understand that the point with coordinates |(x , y)| has undergone this transformation and will henceforth have the coordinates |(x + 2 , y – 1)|: Second, add |2| to its |x|-coordinate and then subtract |1| from its |y|-coordinate.
Here is the translation arrow associated with this rule:
To apply a translation to a figure, it is enough to know the coordinates of the vertices of the initial figure and to apply the translation rule or its arrow to these points.
The vertices of the image figure (final figure) are accompanied by an apostrophe called prime. The vertices |A|, |B|, and |C| become |A’| , |B’| , and |C’|, which is read as “A prime, B prime and C prime”.
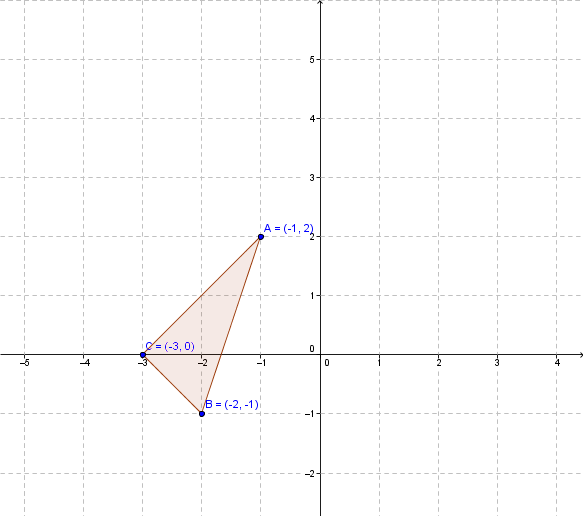
Translate the Triangle Below.
The rule is |t_{(-1,3)}: (x , y) \mapsto (x – 1, y + 3)|.
-
First, write the coordinates of all the vertices:
|A (-1 , 2)|
|B (-2 , -1)|
|C (-3 , 0)| -
Then, apply the rule to each vertex to find the coordinates of the image triangle:
|A (-1 , 2) \mapsto (-1 – 1, 2 + 3)| so |(-2, 5) = A’|;
|B (-2 , -1)\mapsto (-2 – 1, -1 + 3)| so |(-3, 2) = B’|;
|C (-3 , 0)\mapsto (-3 – 1, 0 + 3)| so |(-4, 3) = C’|. -
Finally, draw the new triangle (blue) on the Cartesian plane.
The translation arrow starts from an initial point to an end point and corresponds to the translation defined above: |(x – 1, y + 3)|, i.e., the arrow travels one unit to the left (shift of |x|) and three units up (shift of |y|):
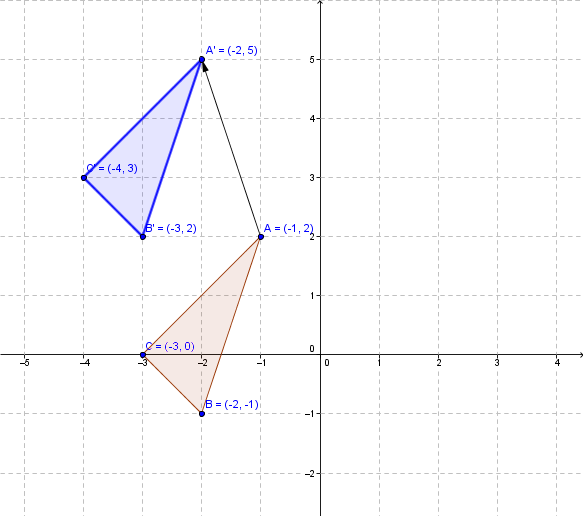
The translation carried out by the translation arrow is completed on each of the vertices of the initial figure.
Clearly, the image figure will be the same whether the translation is carried out using a ruler or the arrow. Indeed, the translation is isometric so it preserves all of the measurements.