<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>On appelle <a href="/fr/eleves/bv/mathematiques/la-translation-m1405"> <strong>translation</strong></a> une transformation géométrique qui associe une figure initiale à une figure image selon trois caractéristiques: une direction, un sens et une longueur.<br>
<br>
La translation d'une figure consiste à faire glisser celle-ci selon une flèche de translation. Cette transformation géométrique est une isométrie. </span></p>
</body></html>
On note une translation par |t| et on indique le glissement horizontal qu'elle fait subir à la figure initiale par |a| et le glissement vertical par |b|.
La règle de transformation est |t_{(a,b)}:(x,y) \mapsto (x+a,y+b)|.
Pour effectuer la translation d'une figure initiale, on applique la règle de transformation à chaque sommet.
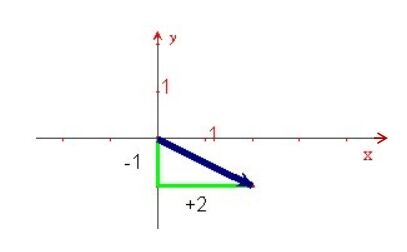
La règle est |t_{(2,-1)} : (x , y) \mapsto (x + 2 , y – 1)|.
On doit comprendre que le point de coordonnées |(x , y)| ayant subi cette transformation sera dorénavant de coordonnées |(x + 2 , y – 1)| : on ajoute |2| à sa coordonnée en |x| et on soustrait |1| à sa coordonnée en |y|.
Voici la flèche de translation reliée à cette règle :
Pour appliquer une translation à une figure, il suffit de connaître les coordonnées des sommets de la figure initiale et d’appliquer sur ces points la règle de translation ou sa flèche.
Les sommets de la figure image (figure finale) sont accompagnés d’une apostrophe que l’on nomme prime. Les sommets |A|, |B| et |C| deviennent |A’|, |B’| et |C’| que l'on peut lire «A prime, B prime et C prime».
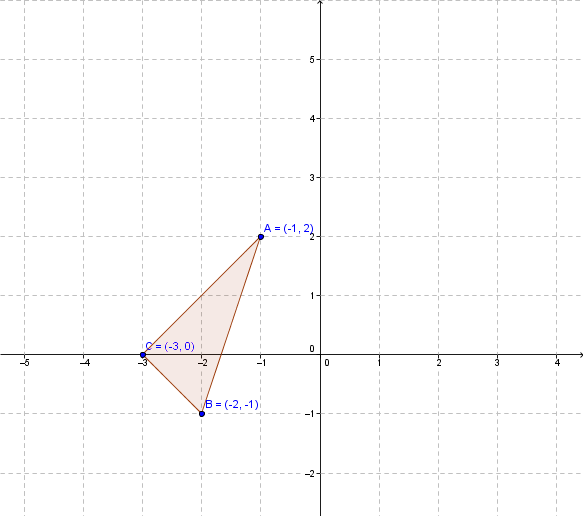
Effectue une translation du triangle ci-dessous.
La règle est |t_{(-1,3)} : (x , y) \mapsto (x – 1, y + 3)|.
Étape 1 : On écrit les coordonnées de tous les sommets :
|A (-1 , 2)|
|B (-2 , -1)|
|C (-3 , 0)|
Étape 2 : On applique la règle sur chaque sommet afin de trouver les coordonnées du triangle image :
|A (-1 , 2) \mapsto (-1 – 1, 2 + 3)| donc |(-2, 5) = A’|;
|B (-2 , -1)\mapsto (-2 – 1, -1 + 3)| donc |(-3, 2) = B’|;
|C (-3 , 0)\mapsto (-3 – 1, 0 + 3)| donc |(-4, 3) = C’|.
Étape 3 : On trace le nouveau triangle (bleu) dans le plan cartésien.
La flèche de translation part d’un point initial à un point final et correspond à la translation définie plus haut : |(x – 1, y + 3)|, c'est-à-dire que la flèche parcourt une unité vers la gauche en |x| et trois unités vers le haut en |y| :
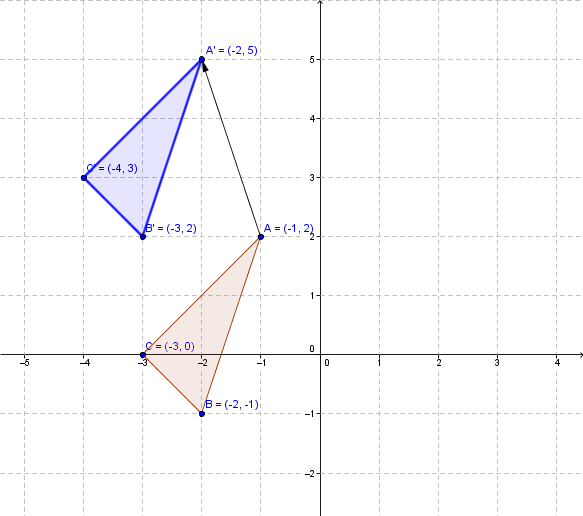
La translation effectuée avec la flèche de translation est réalisée à partir de chacun des sommets de la figure initiale.
Évidemment, la figure image sera la même, que l'on effectue la translation à partir de la règle ou de la flèche. En effet, la translation est une isométrie, elle conserve donc toutes les mesures.