Plane mirrors reflect light rays according to the law of reflection. However, the reflected rays do not converge towards the same point: they move away from each other.
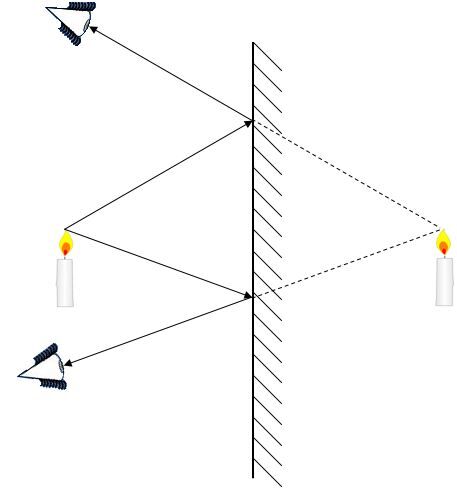
For the eye to perceive an object, the object must emit (or reflect in the case of diffuse reflection) rays in all directions. Our eye perceives that all incoming rays arrive in a straight line, so it sees a virtual image at the point where the extensions of the rays it perceives converge.
Furthermore, the distance between the image and the mirror is equal to the distance between the object and the mirror: the image and the object therefore have the same position in relation to the mirror. Plane mirrors cannot change the size of an object: the image and object are the same size.
As well, the object and the image have the same direction. In the above example with the candle, the candle itself and its image on the other side of the mirror are both upright.
To sum up, the characteristics of the image produced by a plane mirror are as follows: the image is virtual, upright, the same size, and located the same distance from the mirror as the object.
When the driver looks in the rearview mirror, he does not see the actual ambulance behind him, but rather a virtual image of the ambulance in front of him! So, from the driver's point of view, the word ambulance must be legible on this virtual ambulance and not on the real ambulance behind him. In other words, for the driver to be able to read the word, it must be written backwards on the hood of the ambulance.
The law of reflection can be used to determine the position of an image in a plane mirror.
1. Starting at the extremities, draw the rays of light that go all the way to the mirror.
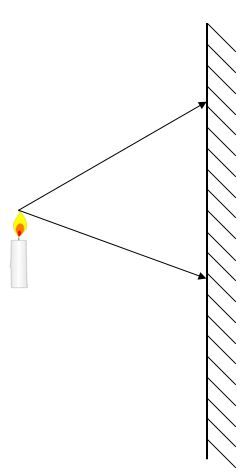
2. Draw the normal line located at the point of incidence for each ray.

3. Draw the reflected rays using the law of reflection.
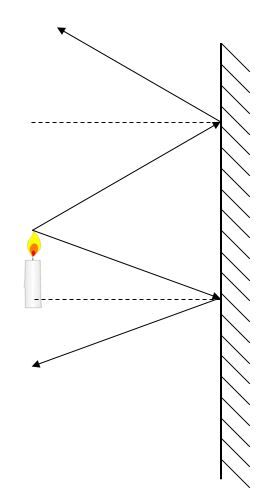
4. Extend the reflected rays to the opposite side of the mirror. Their intersection point represents the starting point of the image.
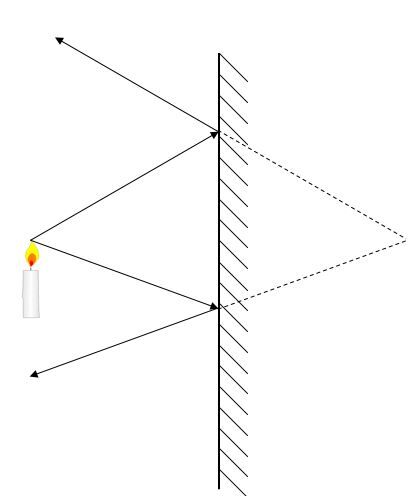
5. Repeat for the rest of the image. Draw the image.

It is also possible to use the law of reflection by drawing light rays at right angles to determine the position of the image. When using light rays that meet the mirror at right angles, the rays will be reflected back onto themselves. However, since there will not be an intersection point, the distance between the object and the mirror must be measured and reproduced on the opposite side of the mirror to find the position of the image.
