Mechanical energy is a concept used in physics to designate the energy of a system stored in the form of kinetic energy and potential energy.
Mechanical energy represents the sum of all the energies existing in a system. In a case where the system encounters no friction force, the law of conservation of energy applies: energy is neither created nor destroyed. However, it could be transferred from one object to another or transformed into other types of energy.
The following image shows the motion of a snowboarder travelling down a half-pipe ramp.
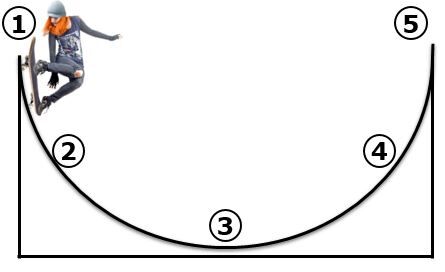
The amount of mechanical energy will always remain the same, because the energy is conserved (assuming there is no friction). However, the type of energy that the rider possesses will vary according to the rider's position and velocity.
By analysing each of the points, it is possible to compare the types of energy used by the snowboarder in her movement.
At point 1, the snowboarder is at the highest point of the halfpipe. She therefore has maximum potential energy. However, since she's just starting to move, she doesn't yet have any kinetic energy.
At point 2, it is halfway down the halfpipe. It has therefore converted some of its potential energy into kinetic energy. However, the mechanical energy remains the same.
At point 3, the potential energy is zero, because the snowboarder is at zero height (on the ground). However, her kinetic energy is at a maximum because she is reaching her highest speed.
At point 4, the snowboarder loses speed but gains height. She has therefore converted some of the kinetic energy she had at point 3 into potential energy. Nevertheless, the mechanical energy remains constant.
At point 5, the rider reaches a height similar to that at point 1, so she has the same amount of potential energy as she did at the start. Since she has the same amount of mechanical energy, her kinetic energy will be zero: she will stop at this point.
Mechanical energy is determined from the following equation:
|E_{m} = E_{p} + E_{k}|
where
|E_{m}| represents the mechanical energy |\small \text {(J)}|
|E_{p}| represents the potential energy |\small \text {(J)}|
|E_{k}| represents the kinetic energy |\small \text {(J)}|
What minimum speed must a salmon have to swim up a waterfall of |\small \text {2,2 m}| ?

The law of conservation of energy means that the mechanical energy at the start of the salmon's motion will be the same as that at the end.
||\begin{align} E_{m_{i}} &= E_{m_{f}} \\
E_{p_{i}} + E_{k_{i}} &= E_{p_{f}} + E_{k_{f}} \end{align}||
At the end of the motion, the salmon will stop at the vertex of the waterfall. Its velocity will be zero (as will its kinetic energy), while the salmon's energy will be in potential form only. This energy comes from the velocity the salmon had at the start, when it was at the bottom of the waterfall.
It is therefore possible to simplify the above formula in order to eliminate null terms.
||\begin{align} 0 + E_{k_{i}} &= E_{p_{f}} + 0 \\
E_{k_{i}} &= E_{p_{f}} \\
\displaystyle \frac {1}{2} \times m \times v^{2} &= m \times g \times \triangle y
\end{align}||
Since mass is present on both sides of the equality, this variable can be simplified. Since the question asks what the speed of the salmon is, all we have to do is isolate the variable to find this speed.
||\begin{align}
\displaystyle \frac {1}{2} \times v^{2} = g \times \triangle y \quad \Rightarrow \quad v &= \sqrt {2 \times g \times \triangle y} \\ &= \sqrt {2 \times \text {9,8 m/s}^2 \times \text {2,2 m}} \\ &= \text {6,57 m/s}
\end{align}||
The salmon has an initial velocity of |\text {6,57 m/s}|.
A cyclist with a mass of |\small \text {63 kg}| is riding down a hill of |\small \text {8 m}| in height after taking a break. He arrives at the foot of the hill with a velocity of |\small \text {12 m/s}|. How much energy has been lost due to friction?

In a situation like the one described above, the conservation of energy is still true: however, the difference between the initial energy and the final energy will have been transformed into a different kind of energy from those present in the mechanical energy formula.
First of all, in calculating the initial energy, the cyclist has potential energy, because he is at the top of the hill. He has no kinetic energy, as he has just taken a break.
||\begin{align}
E_{m_{i}} = E_{p_{i}} + E_{k_{i}} \quad \Rightarrow \quad E_{m_{i}} &= m \times g \times \triangle y + 0 \\
&= \text {63 kg} \times \text {9,8 N/kg} \times \text {8 m} \\ &= \text {4 939,2 J}
\end{align}||
At the bottom of the hill, the cyclist no longer has any potential energy. He does, however, have a significant amount of kinetic energy accumulated, as his velocity is high at the bottom of the hill.
||\begin{align}
E_{m_{f}} = E_{p_{f}} + E_{k_{f}} \quad \Rightarrow \quad E_{m_{f}} &= 0 + \displaystyle \frac {1}{2} \times m \times v^{2} \\
&= \displaystyle \frac {1}{2} \times \text {63 kg} \times \text {(12 m/s)}^{2} \\
&= \text {4 536 J}
\end{align}||
The initial mechanical energy and the final mechanical energy are not equal. This means that the difference in energy has been lost through friction.
||\begin{align}
E = E_{m_{i}} - E_{m_{f}} \quad \Rightarrow \quad
E&= \text {4 939,2 J} - \text {4 536 J} \\
&= \text {403,2 J} \\
\end{align}||
The cyclist has therefore lost |\text {403,2 J}| energy due to friction.
To validate your understanding of the conservation of mechanical energy in an interactive way, consult the following MiniRecup:
