Potential energy is defined as the stored energy that an object possesses due to its position or shape.
It is impossible to observe its effects until this energy is released and transformed into some other form of energy.
In the physics option course, two types of potential energy will be explained in detail.
Gravitational potential energy is defined as the energy stored by an object as a result of its height.
To lift an object, we have to do work, which means transfer energy. To determine the work, multiply the force by the distance. Since work must be done to lift an object, the relationship is the same: for an object to gain height, a force that is equal to its weight (or gravitational force) must be exerted over a distance that is equivalent to the object's vertical displacement. The energy that is thus transferred will then be stored as gravitational potential energy.
The following equation calculates the gravitational potential energy of an object:
|E_{p_{g}} = m \times g \times \triangle y|
where
|E_{p_{g}}| represents gravitational potential energy |\text {(J)}|
|m| represents the mass |\text {(kg)}|
|g| represents the intensity of the gravitational field |\text {(9.8 N/kg)}|
|\triangle y| represents the vertical displacement (height) of the object |\text {(m)}.| It's calculated by finding the difference between the final height of the object and its initial height. |(\triangle y = y_{f} - y_{i}).|
From this formula, we can deduce that the greater the object's mass, the greater its gravitational potential energy. The same applies to height: the higher the object in relation to the ground (or reference point), the greater its gravitational potential energy.
Some editors use the variable |\triangle h| to represent the change (variation) in height. This variable is the same as the |\triangle y| variable used in the formula written above. Using |\triangle y| is preferred, as it more easily represents vertical movement of an object, by referencing its movement along the y-axis.
Positive potential energy represents an increase in potential energy, that is, an increase of the object's height. However, if potential energy is negative, there is a loss of potential energy, which means the object's height decreases.
A |\small \text {50 g}| ball is dropped from the roof of a house. The initial height of the ball is |\small \text {3.5 m}.| What is the variation of potential energy of this ball?
Here's what's known about this problem:
||\begin{align} m &= \text {50 g} = \text {0.050 kg} &g &= \text {9.8 N/kg} \\ y_{i} &= \text {3.5 m} &y_f &= \text {0 m}
\end{align}||
To find the vertical displacement, calculate the difference between the final and initial heights.
||\begin{align}
\triangle y = y_{f} - y_{i} \quad \Rightarrow \quad
\triangle y&= \text {0 m} - \text {3.5 m} \\
&= \text {- 3.5 m} \\
\end{align}||
To calculate the gravitational potential energy:
||\begin{align}
E_{p_{g}} = m \times g \times \triangle y \quad \Rightarrow \quad
E_{p_{g}}&= \text {0.050 kg} \times \text {9.8 N/kg} \times \text {-3.5 m}\\
&= \text {- 1.7 J} \\
\end{align}||
The ball therefore lost | \text {1.7 J}| during its fall. The potential energy was transformed into kinetic energy.
Elastic potential energy is defined as the energy stored in elastic objects (springs, elastics) when they are compressed or stretched relative to their natural position.
To deform an elastic object, a force must be exerted on it over a distance equal to the compression or stretch exerted on the spring or elastic. This energy is stored in the form of elastic potential energy, which can then be transformed when the elastic object is released.
Elastic potential energy can be calculated using the following equation:
|E_{p_{e}} = \displaystyle \frac {1}{2} \times k \times \triangle x^{2}|
where
|E_{p_{e}}| represents the elastic potential energy |\small \text {(J)}|
|k| represents the spring constant |\small \text {(N/m)}|
|\triangle x| represents the displacement of the spring relative to its natural position |\text {(m)}.| It is calculated by finidng the difference between the final and initial positions |(\triangle x = x_{f} - x_{i}).|
From this formula, we can deduce that the greater the compression (or stretch) of the spring, the greater the potential energy of the spring (or elastic). What's more, the higher the spring's spring constant, the higher its elastic potential energy.
Some editors use the variable |\triangle l| to represent spring displacement. This variable is the same as the |\triangle x| variable used in the formula written above.
Any deformation of the spring from rest leads to an increase in elastic potential energy. The amount of energy obtained in the formula will therefore be positive. Any release is therefore represented by a negative sign.
A |\text {10 cm}| long spring (when at rest) is stretched to a length of |\text {15 cm}.| If the spring's spring constant is |\small \text {2500 N/m},| how much energy will be stored in the spring?
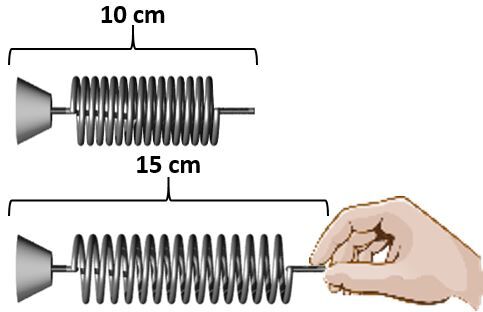
Here's what's known about this problem:
||\begin{align} k &= \text {2500 N/m} &x_f &= \text {15 cm = 0.15 m} \\ x_{i} &= \text {10 cm = 0.10 m} &\triangle x &= x_f - x_i = \text{0.15 m - 0.10 m = 0.05 m}
\end{align}||
To calculate elastic potential energy:
||\begin{align}
E_{p_{e}} = \displaystyle \frac {1}{2} \times k \times \triangle x^{2} \quad \Rightarrow \quad
E_{p_{e}}&= \displaystyle \frac {1}{2} \times \text {2500 N/m} \times \text {(0.05 m)}^{2} \\
&= \text {3.1 J} \\
\end{align}||
When a person works upon an object, they impart potential energy to it. Whether it's lifting a backpack off the ground or compressing a spring, this person exerts a force on the object over a certain distance. Therefore, there's a relationship between the work done on an object and the amount of potential energy it possesses.
|W = \triangle E_{p_{g}}|
|W = \triangle E_{p_{e}}|
where
|W| represents the work |\text {(J)}|
|\triangle E_{p_{g}}| represents the variation of gravitational potential energy |\text {(J)}|
|\triangle E_{p_{e}}| represents the variation of elastic potential energy |\text {(J)}|
