L’énergie potentielle se définit comme étant de l’énergie emmagasinée qu'un objet possède en raison de sa position ou de sa forme.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Il est impossible d’en observer les effets tant et aussi longtemps que cette énergie ne sera pas libérée et transformée en <a href="/fr/eleves/bv/sciences/les-formes-d-energie-s1081">une forme d’énergie</a> quelconque.</p>
<p>Dans le cadre du cours de physique, deux types d'énergie potentielle seront expliqués en détail.</p>
</body></html>
L’énergie potentielle gravitationnelle se définit comme étant de l’énergie emmagasinée par un gain en hauteur que fait un objet.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Pour soulever un objet, il est nécessaire d’effectuer un <a href="/fr/eleves/bv/physique/le-travail-et-la-puissance-p1024">travail</a>, soit un transfert d’énergie. Pour déterminer le travail, il faut multiplier la force par la distance. Puisqu'il faut effectuer un travail pour soulever un objet, la relation sera la même: pour que cet objet gagne en hauteur, il faudra exercer une force égale à son poids (ou <a href="/fr/eleves/bv/physique/la-force-gravitationnelle-p1019">force gravitationnelle</a>) sur une distance équivalente au déplacement vertical de l’objet. L’énergie ainsi transférée sera emmagasinée sous forme d’énergie potentielle gravitationnelle.</p>
</body></html>
L’équation suivante permet de calculer l’énergie potentielle gravitationnelle d’un objet.
|E_{p_{g}} = m \times g \times \triangle y|
où
|E_{p_{g}}| représente l'énergie potentielle gravitationnelle |\text {(J)}|
|m| représente la masse |\text {(kg)}|
|g| représente l'intensité du champ gravitationnel |\text {(9,8 N/kg)}|
|\triangle y| représente le déplacement vertical (hauteur) de l'objet |\text {(m)}|. Elle se calcule en effectuant la différence entre la hauteur finale et la hauteur initiale |(\triangle y = y_{f} - y_{i})|.
De cette formule, on déduit que plus la masse de l'objet est élevée, plus l'énergie potentielle gravitationnelle sera élevée. Il en est de même avec la hauteur: plus l'objet est élevé par rapport au sol (ou au point de référence), plus l'objet aura de l'énergie potentielle gravitationnelle.
Certains éditeurs utilisent la variable |\triangle h| pour représenter la variation de hauteur. Cette variable est la même que la variable |\triangle y| utilisée dans la formule écrite ci-dessus. Toutefois, l'utilisation de |\triangle y| est privilégiée, car elle représente plus facilement un mouvement vertical d'un objet, soit un mouvement suivant l'axe des ordonnées.
Une énergie potentielle positive représente un gain d’énergie potentielle, soit un gain en hauteur d'un objet. Toutefois, si l'énergie potentielle est négative, il y aura une perte d’énergie potentielle qui se traduira par une diminution de la hauteur d'un objet.
On laisse tomber une balle de |\small \text {50 g}| du toit d'une maison. La hauteur de départ de la balle est |\small \text {3,5 m}|. Quelle est la variation d’énergie potentielle de cette balle ?
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>Voici les informations connues dans ce problème.<br>
||\begin{align} m &= \text {50 g} = \text {0,050 kg} &g &= \text {9,8 N/kg} \\ y_{i} &= \text {3,5 m} &y_f &= \text {0 m}<br>
\end{align}||<br>
Pour déterminer le déplacement vertical, on calcule la différence entre la hauteur finale et la hauteur initiale.<br>
||\begin{align} <br>
\triangle y = y_{f} - y_{i} \quad \Rightarrow \quad<br>
\triangle y&= \text {0 m} - \text {3,5 m} \\<br>
&= \text {- 3,5 m} \\<br>
\end{align}||<br>
Pour calculer l'énergie potentielle gravitationnelle:<br>
||\begin{align} <br>
E_{p_{g}} = m \times g \times \triangle y \quad \Rightarrow \quad<br>
E_{p_{g}}&= \text {0,050 kg} \times \text {9,8 N/kg} \times \text {-3,5 m}\\<br>
&= \text {- 1,7 J} \\<br>
\end{align}||<br>
<br>
La balle a donc perdu | \text {1,7 J}| durant sa chute. L’énergie potentielle s’est transformée en <a href="/fr/eleves/bv/physique/l-energie-cinetique-p1028">énergie cinétique</a>.</span></p>
</body></html>
L’énergie potentielle élastique se définit comme étant l’énergie emmagasinée dans des objets élastiques (ressorts, élastiques) lorsque ces derniers sont comprimés ou étirés par rapport à leur position naturelle.
Pour déformer un objet élastique, on doit exercer une force sur cet objet sur une distance égale à la compression ou l'étirement exercé sur le ressort ou l'élastique. C’est sous forme d’énergie potentielle élastique que cette énergie sera emmagasinée et qu'elle pourra par la suite être libérée lorsque l’objet élastique sera relâché.
L'énergie potentielle élastique peut être calculée avec l'équation suivante:
|E_{p_{e}} = \displaystyle \frac {1}{2} \times k \times \triangle x^{2}|
où
|E_{p_{e}}| représente l'énergie potentielle élastique |\small \text {(J)}|
|k| représente la constante de rappel du ressort |\small \text {(N/m)}|
|\triangle x| représente le déplacement du ressort par rapport à sa position naturelle |\small \text {(m)}|. Elle se calcule en effectuant la différence entre la position finale et la position initiale |(\triangle x = x_{f} - x_{i})|.
De cette formule, on déduit que plus la compression (ou l'étirement) du ressort est élevée, plus le ressort (ou l'élastique) possèdera de l'énergie potentielle. De plus, si la constante de rappel du ressort est élevée, l'énergie potentielle élastique sera également plus élevée.
Certains éditeurs utilisent la variable |\triangle l| pour représenter le déplacement du ressort. Cette variable est la même que la variable |\triangle x| utilisée dans la formule écrite ci-dessus.
Toute déformation du ressort à partir du repos entraîne une augmentation de l’énergie potentielle élastique. La quantité d'énergie obtenue dans la formule sera donc positive. Un relâchement représenterait donc un signe négatif.
Un ressort d’une longueur de |\small \text {10 cm}| initialement au repos est allongé pour atteindre une longueur de |\small \text {15 cm}|. Si la constante de rappel du ressort est de |\small \text {2 500 N/m}|, quelle sera l’énergie emmagasinée par le ressort ?
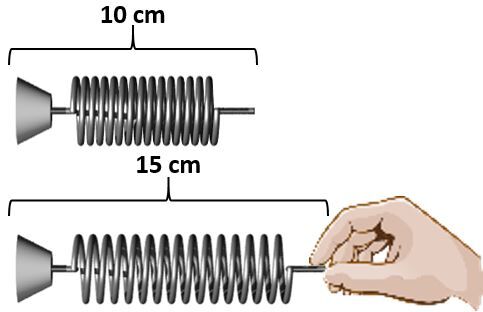
Voici les informations connues dans ce problème.
||\begin{align} k &= \text {2 500 N/m} &x_f &= \text {15 cm = 0,15 m} \\ x_{i} &= \text {10 cm = 0,10 m} &\triangle x &= x_f - x_i = \text{0,15 m - 0,10 m = 0,05 m}
\end{align}||
Pour calculer l'énergie potentielle élastique:
||\begin{align}
E_{p_{e}} = \displaystyle \frac {1}{2} \times k \times \triangle x^{2} \quad \Rightarrow \quad
E_{p_{e}}&= \displaystyle \frac {1}{2} \times \text {2 500 N/m} \times \text {(0,05 m)}^{2} \\
&= \text {3,1 J} \\
\end{align}||
Lorsqu'une personne effectue un travail sur un objet, elle lui confère de l'énergie potentielle. Que ce soit en soulevant un sac à dos du sol ou en poussant sur un ressort pour le comprimer, cette personne exerce une force sur l'objet sur une certaine distance. Il existe donc une relation entre le travail effectué sur un objet et la quantité d'énergie potentielle que possède un objet.
|W = \triangle E_{p_{g}}|
|W = \triangle E_{p_{e}}|
où
|W| représente le travail |\small \text {(J)}|
|\triangle E_{p_{g}}| représente la variation d'énergie potentielle gravitationnelle |\small \text {(J)}|
|\triangle E_{p_{e}}| représente la variation d'énergie potentielle élastique |\small \text {(J)}|
