The Snell-Descartes law is a mathematical equation making it possible to calculate the incident and refracted angles as well as the absolute refractive indices of the medium present.
Before analyzing Snell-Descartes' law, it is necessary to understand the vocabulary used in light phenomena involving refraction.
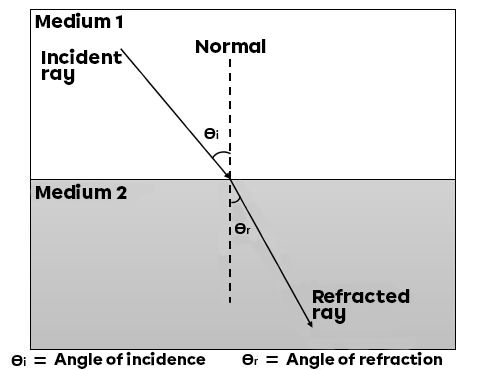
Vocabulary Associated with Refraction Between Two Mediums
| Incident ray | A ray of light that is directed towards a surface. |
| Incidence medium – Medium 1 | First medium crossed by light. |
| Refracted ray | Ray that has been deflected by a surface. |
| Refractive medium – Medium 2 | Second medium crossed by the light. |
| Normal | Line perpendicular at any point to a surface. |
| Angle of incidence – |\theta_{i}| | Angle between the incident ray and the normal. |
| Angle of refraction – |\theta_{r}| | Angle between the refracted ray and the normal. |
The law of refraction requires two elements: the refracted ray is in the same plane as the incident ray and the normal. In addition, the relationship between the refractive indexes of the two mediums and the angles of incidence and refraction follows the law of Snell-Descartes.
Snell-Descartes law is determined by the following equation:
|n_{1}\times \sin \theta_{i} = n_{2}\times \sin\theta_{r}|
where
|n_{1}| represents the refractive index of the incident ray
|\theta_{i}| represents the angle of incidence |\small (^{\circ})|
|n_{2}| represents the refractive index of the reflected ray
|\theta_{r}|represents the angle of refraction |\small (^{\circ})|
A ray from the ice |\left( \small n = 1.31 \right)| passes through a sheet of plexiglass. We measure an angle of incidence of |\small 27^{\circ}| and an angle of refraction of |\small 23^{\circ}|. What is the refractive index of the plexiglass?
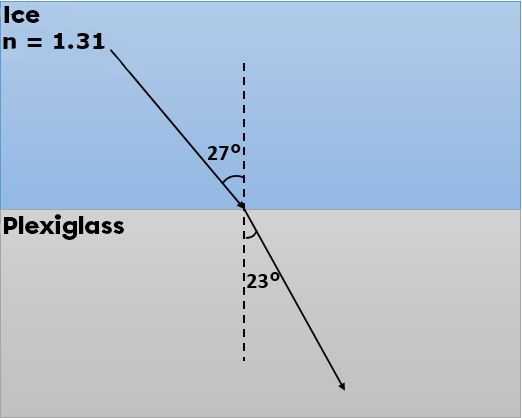
||\begin{align}n_{1} &= 1.31 &\theta_{i} &= 27^\circ\\
n_{2} &= ?& \theta_{r} &= 23^\circ\\ \end{align}||
Using the Snell-Descartes relation:
||\begin{align} n_{1} \times \sin \theta_{i} = n_{2} \times \sin \theta_{r} \quad \Rightarrow \quad n_{2} &=
\frac {n_{1} \times \sin \theta_{i}}{\sin \theta_{r}} \\ \\
&= \frac{1.31 \times \sin 27^{\circ}}{\sin 23^\circ}\\ \\
&= 1.52 \end{align}||
Therefore, the refractive index of the second medium is |1.52|.
Always consider the angles in relation to the normal, and not in relation to the surface of the medium.
It is important to put your calculator in degrees mode rather than radians mode when the Snell-Descartes law is used.