La loi de Snell-Descartes est une équation mathématique permettant de calculer les angles incidents et réfractés ainsi que les indices de réfraction absolus des milieux en présence.
Avant d’analyser la loi de Snell-Descartes, il est nécessaire de comprendre le vocabulaire utilisé dans les phénomènes lumineux impliquant la réfraction.
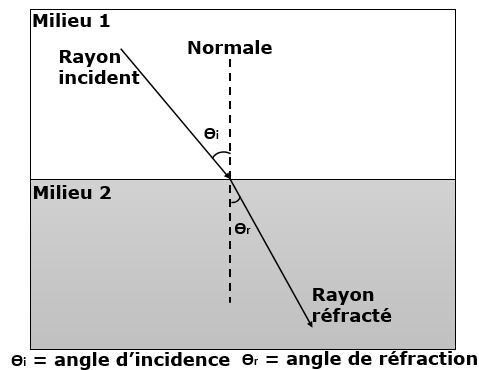
Vocabulaire associé à la réfraction entre deux milieux
| Rayon incident | Rayon lumineux qui se dirige vers une surface. |
| Milieu d'incidence - Milieu 1 | Premier milieu traversé par la lumière. |
| Rayon réfracté | Rayon qui a été dévié par une surface. |
| Milieu de réfraction - Milieu 2 | Second milieu traversé par la lumière. |
| Normale | Droite perpendiculaire en tout point à une surface. |
| Angle d'incidence - |\theta_{i}| | Angle situé entre le rayon incident et la normale. |
| Angle de réfraction - |\theta_{r}| | Angle situé entre le rayon réfracté et la normale. |
La loi de la réfraction nécessite deux éléments: le rayon réfracté est dans le même plan que le rayon incident et la normale. De plus, la relation liant les indices de réfraction des deux milieux et les angles d'incidence et de réfraction suit la loi de Snell-Descartes.
La loi de Snell-Descartes est déterminée par l'équation suivante :
|n_{1}\sin \theta_{i} = n_{2}\sin\theta_{r}|
où
|n_{1}| représente l'indice de réfraction du milieu traversé par le rayon incident
|\theta_{i}| représente l'angle d'incidence |(^{\circ})|
|n_{2}| représente l'indice de réfraction du milieu traversé par le rayon réfléchi
|\theta_{r}|représente l'angle de réfraction |(^{\circ})|
Un rayon provenant de la glace |\left( \small n = 1,31 \right)| traverse un morceau de plexiglas. On mesure un angle d'incidence de |\small 27^{\circ}| et un angle de réfraction de |\small 23^{\circ}|. Quel est l’indice de réfraction du morceau de plexiglas ?
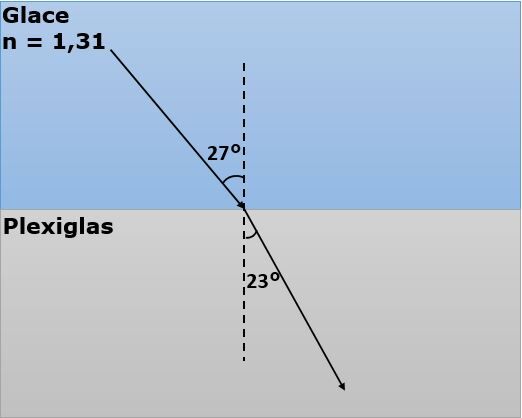
||\begin{align}n_{1} &= 1,31 &\theta_{i} &= 27^\circ\\
n_{2} &= ?& \theta_{r} &= 23^\circ\\ \end{align}||
En utilisant la relation de Snell-Descartes:
||\begin{align} n_{1} \times \sin \theta_{i} = n_{2} \times \sin \theta_{r} \quad \Rightarrow \quad n_{2} &=
\frac {n_{1} \times \sin \theta_{i}}{\sin \theta_{r}} \\ \\
&= \frac{1,31 \times \sin 27^{\circ}}{\sin 23^\circ}\\ \\
&= 1,52 \end{align}||
L'indice de réfraction du deuxième milieu est donc |1,52|.
Il faut toujours considérer les angles par rapport à la normale, et non par rapport à la surface du milieu.
Il est important de mettre sa calculatrice en mode degrés plutôt qu'en mode radians lorsque la loi de Snell-Descartes doit être utilisée.