The resultant force, or net force, is the force obtained by the vector addition of all the forces acting on an object.
A resultant force is equivalent to all the forces applied to the object. To determine the resultant force, we need to take into account the intensity, direction and orientation of the forces involved.
Three horses are pulling on a tree as shown below (each horse is represented by a force : |F_1|, |F_2| et |F_3|). In which direction will the tree fall? What force will be exerted on the tree?
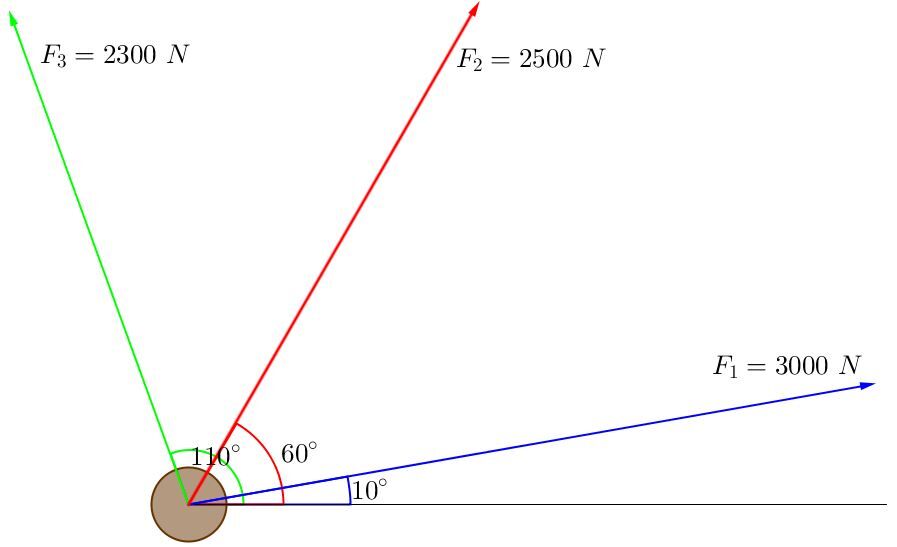
To determine the resultant force, the vectors need to be added together. The components method is the preferred method for this, as it converts polar coordinates into Cartesian coordinates. The components can then be added together (the x-components together and the y-components together) to determine the norm and orientation of the resulting vector.
First, the vectors need to be broken down into their components.
| |
Horizontal component |
Vertical component |
| |\color {blue} {F_1}| | |3\:000 \: \text {N} \times \cos 10^{\circ} = 2\:954 \: \text {N}| | |3\:000 \: \text {N}\times \sin 10^{\circ} = 521 \: \text {N}| |
| |\color {red} {F_2}| | |2\:500 \: \text {N}\times \cos 60^{\circ} = 1\:250 \: \text {N}| | |2\:500 \: \text {N}\times \sin 60^{\circ} = 2\:165 \: \text {N}| |
| |\color {green} {F_3}| | |2\:300 \: \text {N} \times \cos 110^{\circ} = -787 \: \text {N}| | |2\:300 \: \text {N}\times \sin 110^{\circ} =2\:161 \: \text {N}| |
Once the three vectors have been decomposed, the horizontal components of each of the vectors should be added together, and the same should be done with the vertical components.
| | Horizontal component | Vertical component |
| |\color {blue} {F_1}| | |2\:954 \: \text {N}| | |521\: \text {N}| |
| |\color {red} {F_2}| | |1\:250 \: \text {N}| | |2\:165 \: \text {N}| |
| |\color {green} {F_3}| | |-787 \: \text {N}| | |2\:161 \: \text {N}| |
| |\text {Sum}| | |2\:954+ 1\:250 + -787 = 3\:417 \: \text {N}| | |521+ 2\:165 + 2\:161 = 4\:847 \: \text {N}| |
From the components obtained, we then need to reconstruct a vector by determining its norm and orientation. Cartesian coordinates must therefore be transformed into polar coordinates.
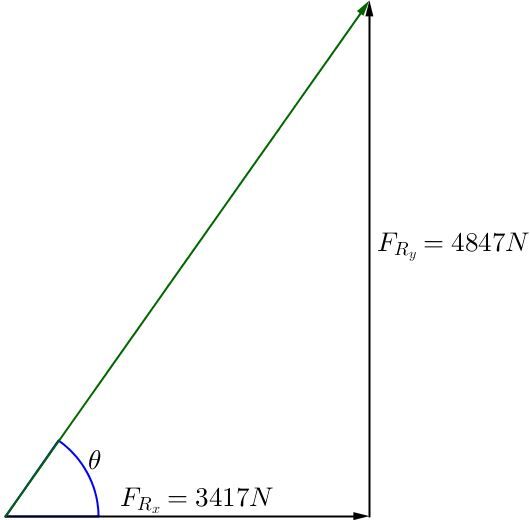
To determine the norm, use the Pythagorean theorem.
||\begin{align} F_r = \sqrt{{F_x}^2 + {F_y}^2} \quad \Rightarrow \quad r &= \sqrt{ {(3\:417 \: \text{N})^2} + {(4\:847 \: \text{N})^2}} \\ &= \sqrt{35\:169\:298}\\ & \approx 5930 \: \text{N} \end{align}||
Trigonometry is used to determine orientation.
||\begin{align} \theta=\tan^{-1} \left(\frac{ {y}}{ {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} = \left( \frac{ {4\:847 \: \text{N}}}{{3\:417\: \text{N}}} \right)\\
&= \tan^{-1}\left(1.418...\right)\\
& \approx 54.8^{\circ}\end{align}||
The resulting force is therefore |5\:930\:\text {N}| at |54.8^{\circ}|. In the context of the problem, if one horse exerted such a force, it would produce the same result as the three horses in the scenario above.
The balancing force, or equilibrant force, is the force that must be added to a system of forces so that the sum of the forces is equal to zero.
In other words, the balancing force is the force that cancels out the resultant force. The object thus retains its inertia. It is of the same magnitude as the resultant force, but is exerted in the opposite direction. There are two options for reversing the direction of the resultant force, depending on the type of coordinates presented:
-
If the polar coordinates (norm and orientation) are known, you will need to add |\small 180^{\circ}| to the orientation of the resultant vector (if the orientation of the resultant vector is less than |\small 180^{\circ}|) or subtract |\small 180^{\circ}| (if the orientation of the resultant vector is greater than or equal to |\small 180^{\circ}|).
-
If the Cartesian coordinates (x and y components) are known, the sign of each component must be changed.
In the previous example, the balancing force would be |\small 5\:930\:\text {N}| to |\small 234,8^{\circ}| (polar coordinates) or |\left( \small -3\: 417 \: \text {N}, -4\: 847 \text {N} \right)| in Cartesian coordinates.