Adding or subtracting vectors results in a new vector called the resultant vector (or resultant).
Several methods are used to add vectors. When the vectors are in a plane, the triangle method or parallelogram method can be used. Vectors can also be added algebraically using the algebraic method. Finally, in some cases, Chasles' relation can be used.
The sum of vectors |\overrightarrow{u}| and |\overrightarrow{v}| is defined by the following resultant vector.||\overrightarrow{u}+\overrightarrow{v}||
As its name suggests, the triangle method consists of obtaining a resultant vector by forming a triangle in a Cartesian plane.
-
Place the vectors one after the other so the end of the first vector becomes the origin of the second.
-
Draw the resultant vector by connecting the origin of the first vector to the end of the second.
Determine the resultant of the sum of the following vectors.
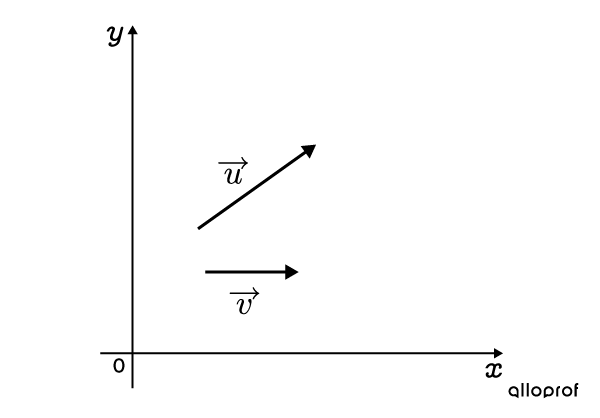
-
Place the vectors one after the other
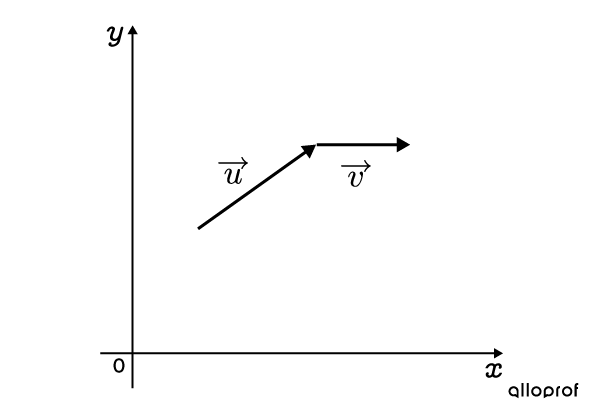
-
Draw the resultant vector

The resultant is the green vector, obtained after adding |\overrightarrow {u}| and |\overrightarrow {v}.|
The parallelogram method can be used when the vectors have the same origin. The resultant is the diagonal of the parallelogram formed.
-
Place |\overrightarrow{u}| and |\overrightarrow{v}| so they have the same origin.
-
Draw another |\overrightarrow{u}| at the end of |\overrightarrow{v}.|
-
Draw another |\overrightarrow{v}| at the end of |\overrightarrow{u}.|
-
Draw the resultant vector that starts at the origin and goes to the opposite vertex of the parallelogram formed.
Determine the resultant of the sum of the following vectors.
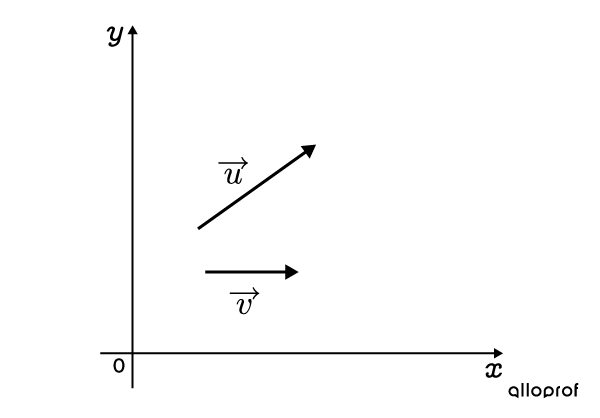
-
Place |\overrightarrow{u}| and |\overrightarrow{v}| so they have the same origin
Moving |\overrightarrow{v},| gives the following representation.
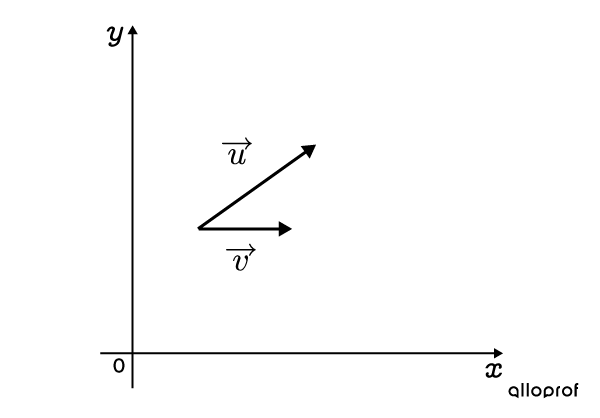
-
Draw another |\overrightarrow{u}| at the end of |\overrightarrow{v}|
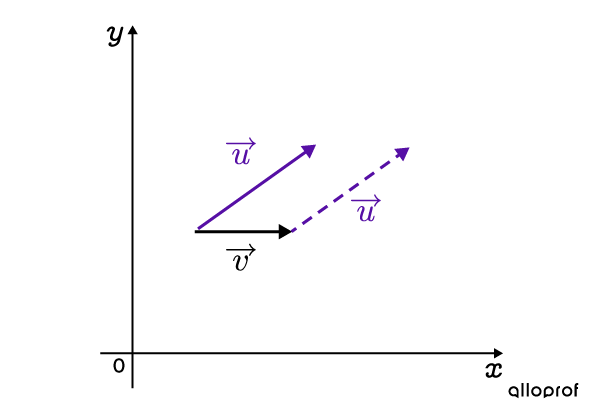
-
Draw another |\overrightarrow{v}| at the end of |\overrightarrow{u}|
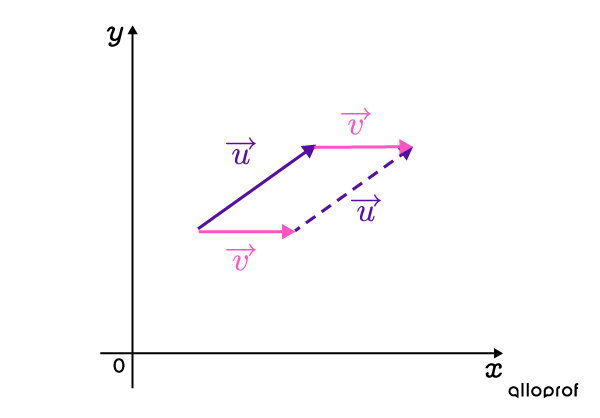
-
Draw the resultant vector

The resultant is the green vector, obtained after adding |\overrightarrow {u}| and |\overrightarrow {v}.|
To add vectors algebraically, add the components of the vectors to obtain the components of the resultant vector.
Let |\overrightarrow{u}=(a,b)| and |\overrightarrow{v}=(c,d),| therefore:||\begin{align}\overrightarrow {u}+\overrightarrow{v}&= (\color{#EC0000}a,\color{#3B87CD}b)+(\color{#EC0000}c, \color{#3B87CD}d)\\&=(\color{#EC0000}a+\color{#EC0000}c,\color{#3B87CD}b+ \color{#3B87CD}d)\end{align}||
-
Add the components in |x| and in |y| of each vector.
-
Determine the components of the resultant vector.
Let |\overrightarrow{u}=(3, 2)| and |\overrightarrow{v}=(4, -1).| What is the resultant of the sum of the two vectors?
-
Add the components in |x| and |y| of each vector||\begin{align}\overrightarrow {u}+\overrightarrow{v}&= (\color{#EC0000}3,\color{#3B87CD}2)+(\color{#EC0000}4, \color{#3B87CD}{-1})\\&=(\color{#EC0000}3+\color{#EC0000}4,\color{#3B87CD}2+ \color{#3B87CD}{-1})\\&=(7,1)\end{align}||
-
Determine the components of the resultant vector
Components |(x,y)| of the resultant are |(7,1).|
To add vectors using Chasles’ relation, the starting and ending points of the vectors must be identified by letters. Chasles' relation is useful during vector demonstrations.
Two vectors can be added using Chasles’ relation when the extremity of the first vector matches the origin of the second. The sum is then equal to the vector with the origin of the first vector and the extremity of the second.||\overrightarrow{A\color{#FF55C3}{B}}+\overrightarrow{\color{#FF55C3}BC}=\overrightarrow{AC}||
The following example demonstrates an instance when Chasles’ relation can be applied.
What is the vector resulting from adding vectors |\overrightarrow{RS}| and |\overrightarrow{TR}?|
Note that point |R| is the first vector’s origin and the second vector’s extremity. Vector addition is commutative, therefore, the order of vector addition can be changed, causing the endpoint of the first to match the origin of the second.||\overrightarrow{RS}+\overrightarrow{TR}=\overrightarrow{TR}+\overrightarrow{RS}|| We now have the correct form to apply Chasles’ relation. We obtain:||\overrightarrow{T\color{#FF55C3}{R}}+\overrightarrow{\color{#FF55C3}RS}=\overrightarrow{TS}|| The resultant of the sum of the vectors |\overrightarrow{RS}| and |\overrightarrow{TR}| is vector |\overrightarrow{TS}.|
Subtracting a vector is equivalent to adding its opposite vector.
Subtracting |\overrightarrow{u}| and |\overrightarrow{v}| results in:||\overrightarrow{u}-\overrightarrow{v}=\overrightarrow{u}+(-\overrightarrow{v})|| This image illustrates adding and subtracting |\overrightarrow{u}| and |\overrightarrow{v}.|
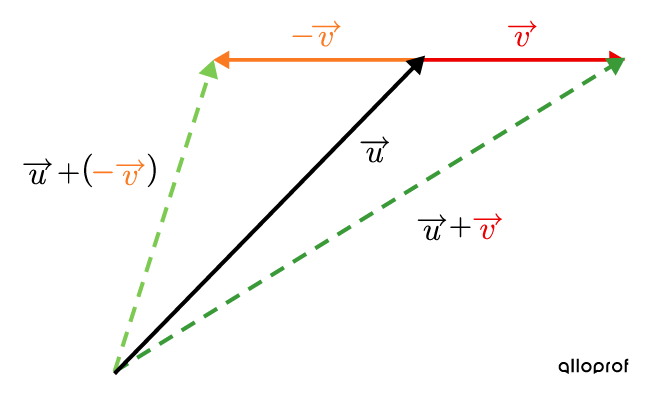
After changing subtraction to addition, the triangle or parallelogram method can be used to obtain the resultant vector in a plane.
To subtract vectors algebraically, add the components of the first vector with the opposite of the components of the second vector.
Let |\overrightarrow{u}=(a,b)| and |\overrightarrow{v}=(c,d),| therefore:||\begin{align}\overrightarrow {u}-\overrightarrow{v}&=\overrightarrow {u}+(-\overrightarrow{v})\\&= (\color{#EC0000}a,\color{#3B87CD}b)+(-\color{#EC0000}c, -\color{#3B87CD}d)\\&=(\color{#EC0000}a-\color{#EC0000}c,\color{#3B87CD}b-\color{#3B87CD}d)\end{align}||
-
Add the components of the first vector with the opposite of the components of the second vector.
-
Determine the components of the resultant vector.
Let vector |\overrightarrow{u}=(3,2)| and vector |\overrightarrow{v}=(4,-1).| What's the value of |\overrightarrow{u}-\overrightarrow{v}?|
-
Add the components of the first vector with the opposite of the components of the second vector||\begin{align}\overrightarrow {u}-\overrightarrow{v}&=(\color{#EC0000}a,\color{#3B87CD}b)+(-\color{#EC0000}c,-\color{#3B87CD}d)\\&=(\color{#EC0000}3,\color{#3B87CD}2)+(-\color{#EC0000}4,-\color{#3B87CD}{-1})\\&=(\color{#EC0000}3-\color{#EC0000}4,\color{#3B87CD}2+\color{#3B87CD}{1})\\&=(-1,3)\end{align}||
-
Determine the components of the resultant vector
Components |(x,y)| of the resultant are |(7, 1).|
Using the starting and ending point of the vectors, and the definition of vector subtraction, the subtraction is written as follows.||\begin{align}\overrightarrow{AB}-\overrightarrow{CD}&=\overrightarrow{AB}+(-\overrightarrow{CD})\\&=\overrightarrow{AB}+\overrightarrow{DC}\end{align}|| The last example makes it possible to use Chasles’ relation in specific cases.
What is the vector resulting from the subtraction |\overrightarrow{AC}-\overrightarrow{BC}?|
Since subtracting is the same as adding the opposite vector, the result is:||\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB}|| As the extremity of the first vector equals the origin of the second, we can apply Chasles’ relation.||\overrightarrow{A\color{#FF55C3}{C}}+\overrightarrow{\color{#FF55C3}CB}=\overrightarrow{AB}||The resultant of subtracting vectors |\overrightarrow{AC}| and |\overrightarrow{BC}| is vector |\overrightarrow{AB}.|
To validate your understanding about vectors interactively, consult the following CrashLesson:
