Friction is a force created by the interaction of two surfaces in contact sliding over each other and which oppose the movement.
Friction is caused by irregularities on a surface. Although a surface may appear smooth to the naked eye, small asperities (irregularities) are present on the surface of an object when viewed under a microscope.
There are a number of factors that influence the force of friction. We need to consider the types of surface that are in contact. Smooth surfaces generally create less friction than rough ones.
Two blocks of wood create a weaker friction force than a piece of wood and sandpaper.
The normal force must also be considered. This force is directly related to the gravitational force, since it is generally an action-reaction force. The greater the normal force, the greater the frictional force.
An object on a flat surface whose mass is |10 kg| has a greater normal force than a similarly shaped object on the same flat surface whose mass is just |5 kg| because the normal force created on the first object is greater than that on the second.
Since force of friction is a force that opposes the motion of an object, it is calculated by determining the difference between the driving force and the resultant force.
The force of friction is calculated using the following formula:
||F_f = F_d - F_R||
where
|F_f| represents the force of friction (N)
|F_m| represents the driving force (N)
|F_R| represents the resultant force (N)
Static friction is a force of friction that prevents an object from moving.
Kinetic friction is a force of friction that is present when an object is in motion against another object.
Static friction is a synonym for adhesion. In this case, the static friction force prevents sliding (or motion between the two objects). When an object starts moving, this means that the driving force exerted on the object is greater than the static friction force. When the object is travelling, the kinetic friction force is equal to the driving force needed to keep the object at a constant velocity. So, a stationary object on which a driving force is exerted initially produces static friction, but as soon as the object starts moving, the force of friction is kinetic.

The graph above shows what happens when a stationary object is set in motion. At the start, the friction force is static, because the object is stationary. As soon as the applied tension force becomes greater than the static friction force, the object starts to move. The force of friction starts to rapidly decrease (a phase known as adhesion slip) and then becomes constant. The force of friction, which is now kinetic, is equal to the applied tension force, in order to maintain the object's state of motion.
The coefficient of static friction is the ratio between the static friction force of an object and the normal force.
The coefficient of kinetic friction is the ratio between the kinetic friction force of an object and the normal force.
The coefficients of friction are constant values that have been established experimentally and depend solely on the surfaces in contact. There are reference tables for determining the static and kinetic coefficients for certain materials. Here are some useful coefficients:
|
Material |
Static coefficient |
Kinetic coefficient |
| Velcro-Velcro | |6.0| | |5.9| |
| Aluminium-Aluminium | |1.4| | |1.2| |
| Glass-Glass | |1.0| | |0.40| |
|
Rubber-Dry concrete |
|1.0| | |0.70| |
|
Rubber-Wet concrete |
|0.60| | |0.50| |
|
Rubber-Asphalt |
|0.85| | |0.67| |
|
Steel-Steel |
|0.75| | |0.57| |
|
Leather-Wood |
|0.61| | |0.52| |
| Wood-Wood | |0.58| | |0.40| |
|
Copper-Steel |
|0.53| | |0.36| |
| Ski-Snow | |0.14| | |0.05| |
|
Steel-Ice |
|0.10| | |0.05| |
These coefficients are used to determine the force of friction exerted on an object, whether stationary or in motion.
The equation used to calculate a force of friction is as follows:
||F_f=\mu \cdot F_N||
where
|F_f| represents the force of friction (N)
|\mu| represents the coefficient of friction (no units)
|F_N| represents the normal force (N)
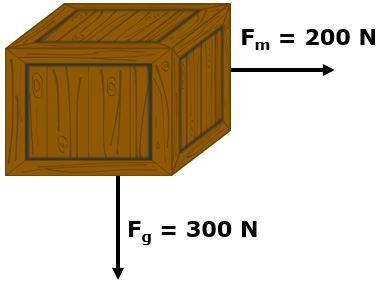
An attempt is made to set a wooden box weighing 300 N in motion on a hardwood floor, using a force of 200 N. Will the box start to move? If it does move, what will the kinetic friction force be?
First, the maximum static friction force must be determined. To do so, we first need to determine the normal force. Since the box exerts a downward force of 300 N due to the gravitational force, the floor will react by exerting a force of 300 N towards the box, which will represent the normal force. The table above shows that the coefficient of static friction between wood and wood is |0.58.| Therefore,
||\begin{align}
F_{f_s} & = && \mu_s && \cdot && F_N \\
&= && 0.58 && \cdot && 300 \ N \\
& = && 174 \ N \end{align}||
A force of |200 \ N| is therefore sufficient to set the box in motion despite the static friction force.
To determine the kinetic friction force, the formula is the same. However, the coefficient of kinetic friction of |0.40| must be used:
||\begin{align}
F_{f_k}& = && \mu_k && \cdot && F_N \\
& = && 0.40 && \cdot && 300 \ N \\
& = && 120 \ N \end{align}||