The uniformly accelerated rectilinear motion (UARM) variables are position (distance travelled or displacement), speed, acceleration and time. Equations are determined about UARM from the variables and from the graphs produced that use them.
| |v_{avg}=\displaystyle \frac{\triangle x}{\triangle t}| | |a=\displaystyle \frac{\triangle v}{\triangle t}| |
| |v_{f}=v_{i} + a \cdot {\triangle t}| | |\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}| |
| |\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}| | |{v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x| |
In the formulas, the following variables are used:
| Variable | Definition | Units |
|---|---|---|
| |\triangle x = x_{f} - x_{i}| | Position variation (distance travelled or displacement) = End position - initial position |
Metres |\text {(m)}| |
| |v_{\text{moy}}| | Average speed | Metres per second |\text {(m/s)}| |
| |v_{i}| | Initial speed | Metres per second |\text {(m/s)}| |
| |v_{f}| | Final speed | Metres per second |\text {(m/s)}| |
| |a| | Acceleration | Metres per second squared|\text {(m/s}^2)| |
| |\triangle t = t_{f} - t_{i}| | Time variation = End time - start time | Seconds |\text {(s)}| |
Some notation editors use the variable |\triangle S| to represent the change in position. The variable is the same as the |\triangle x| variable, which is used in the formulas written above. However, the use of |\triangle x| is recommended because it better represents a horizontal movement (i.e.,a movement along the x-axis).
In addition, the variable |\triangle y| can be used to define the variation of position in a vertical movement of an object (i.e., a movement along the y-axis)
To correctly use the equations, it is necessary to use the signs associated with the variables. By locating the frame of reference correctly at the start of a problem, the signs of the different variables are easier to determine.
Comparing two moving bodies
A car initially at point A is heading to the right with a constant speed of |\small \text {15 m/s}|. Starting from point B, another car, initially at rest, moves to the left with an acceleration of |\small \text {2.5 m/s}^2|.
Points A and B are separated by a distance of |\small \text {250 m}|. How long will it take for the two cars to cross paths?
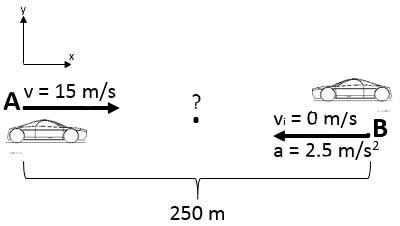
We must first establish a frame of reference for this type of problem. It was located at point A, and it is oriented to the right. Next, you need to know that the two cars meet at the same point; therefore, it is necessary to determine the final position ( |x_{f}| ).
First, consider vehicle A. Since the speed is constant, the initial speed, the final speed and the average speed are the same.
||v_{i} = v_{f} = v_{\text{avg}} = 15 \: \text {m/s} \\ \begin{align}
&x_{i} = 0 \: \text {m} &x_{f} &= ? \end{align}||
The relationship of speed versus time for vehicle A is described below.
||\begin{align} v_{\text{avg}} = \displaystyle \frac{\triangle x}{\triangle t}
\quad \Rightarrow \quad
v_{\text{avg}} &= \displaystyle \frac{x_{f} - x_{i}}{\triangle t} \\
15 \: \text {m/s} &= \displaystyle \frac{x_{f} - 0 \: \text {m}}{\triangle t}\\
x_{f} &= 15 \: \text {m/s} \cdot \triangle t \end{align}||
Now, let’s consider vehicle B.
||\begin{align}x_{i} &= 250 \: \text {m} &a &= -2.5 \: \text {m/s}^2\\
v_{i} &= 0 \: \text {m/s} \end{align}||
It is possible to determine the relation for vehicle B.
||\begin{align} \triangle x = v_{i} \cdot \triangle t + \displaystyle \frac {1}{2} \cdot a \cdot \triangle t^2
\quad \Rightarrow \quad
\triangle x &= 0 \: \text {m/s} \cdot \triangle t + \displaystyle \frac {1}{2} \cdot (-2.5 \: \text {m/s}^2) \cdot \triangle t^{2} \\
x_{f} - 250 \: \text {m} &= 0 -1.25 \cdot \triangle t^{2}\\
x_{f} &= -1.25 \cdot \triangle t^{2} + 250 \end{align}||
When the two vehicles cross paths, they will have the same final position and they will cross paths at the same time.
Therefore, it is possible to solve the problem by using a system with two equations that have two unknowns with the comparison method.
||\begin {align} x_{f,A}&= x_{f,B} \\
15 \cdot \triangle t &= -1.25 \cdot \triangle t^{2} + 250 \\
0 &=-1.25 \cdot \triangle t^2 - 15 \cdot \triangle t + 250 \end{align}||
It is now possible to determine the zeros of the quadratic function for determining the time elapsed before the cars meet.
||\begin {align} t_{1.2} = \displaystyle \frac{-b\pm\sqrt{b^2-4ac}}{2a} \quad \Rightarrow \quad \displaystyle t_{1.2} &= \frac{-(-15)\pm\sqrt{(-15)^2-4(-1.25)(250)}}{2(-1.25)} \\
t_{1.2} &= \frac{15\pm\sqrt{225+1\:250}}{-2.50} \\
t_{1.2} &= \frac{15\pm\sqrt{1475}}{-2.50} \\
t_{1} &= \frac{15+ 38.41}{-2.50} = -21.4 \: \text {s} \\
t_{2} &= \frac{15- 38.41}{-2.50} = 9.4 \: \text {s}
\end{align}||
Only a positive value is possible in the problem. Therefore, the two vehicles will meet after |9.4 \: \text {s}|.
Using the frame of reference correctly
A car travelling at |\small 30 \: \text {m/s}| brakes at a rate of |\small -4 \: \text {m/s}^2| over a distance of |\small 35 \: \text {m}|. What is its final speed?
The first step is to identify the variables.
||\begin{align}a &= -4 \: \text {m/s}^2 &v_{i} &= 30 \: \text {m/s}\\
\triangle x &= 35 \: \text {m} \end{align}||
To solve the problem, one of the equations of UARM must be used.
||\begin{align} {v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x
\quad \Rightarrow \quad
{v_{f}}^2&={(30 \: \text {m/s})}^2+2 \cdot (- 4\: \text {m/s}^2) \cdot (35 \: \text {m}) \\
{v_{f}}^2&=900 - 280\\
{v_{f}}^2&=620 \\
{v_{f}} &= \pm \: 24.9 \: \text {m/s}\end{align}||
Of these two values, only the positive one one possible, since the negative value means the car would not have stopped moving forward, and would also have reached a speed of |\small 24.9 \: \text {m/s}| in the opposite direction. You have to be vigilant to correctly choose the right value: the decision must be made according to the context of the problem.
Therefore, the final speed is |24.9 \: \text {m/s}| in the direction of the initial movement.
Pour valider ta compréhension à propos du MRUA de façon interactive, consulte la MiniRécup suivante :
