Total internal reflection occurs when the angle of the refracted ray is greater than |\text {90}^{\circ}.|
At this point, the incident ray can no longer penetrate the second medium. Instead, the ray undergoes a reflection on the surface that separates the two mediums, according to the laws of reflection.
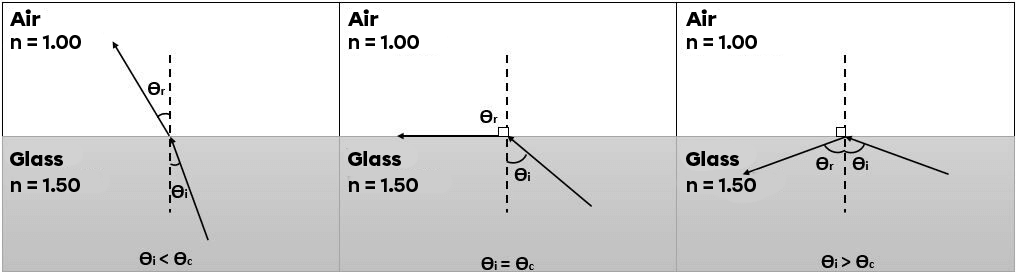
There are two conditions that must be satisfied for total internal reflection to occur:
The index of refraction of the incident medium must be greater than that of the refracted medium (|n_{1} > n_{2}|).
The angle of incidence must be greater than the critical angle (|\theta_{i} > \theta_{c}|).
In the example below, the incident ray passes through water and into air. The first condition of total internal reflection is therefore satisfied, since the index of refraction the first medium, water, is higher than that of the second medium, air. If the angle of incidence is greater than the critical angle, the incident ray will reflect as if it were striking the surface of a mirror.

The critical angle is the incident angle which causes the ray to be refracted at a |\small \text {90}^{\circ}| angle into the refracting medium.
The critical angle can be seen in the image below. In this situation, the angle of incidence is equal to the critical angle.
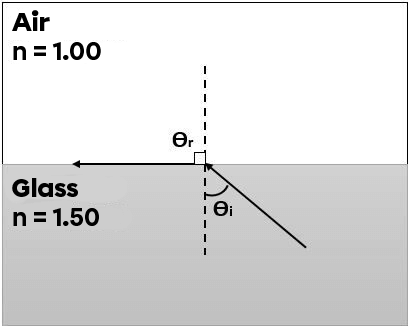
The Snell-Descartes law can be used to derive the following equation that allows us to mathematically determine the critical angle. Since the angle of refraction is |\text {90}^{\circ},| we can isolate the unknown variable, or the angle of incidence (which is equivalent to the critical angle):
||\begin{align} n_{1}\times \sin \theta_{i} = n_{2}\times \sin\theta_{r} \quad \Rightarrow \quad n_{1}\times \sin \theta_{c} &= n_{2}\times \sin 90^{\circ} \\
n_{1}\times \sin \theta_{c} &= n_{2}\times 1 \\
\sin \theta_{c} &= \frac {n_{2}}{n_{1}} \end{align}||
The formula to calculate the critical angle is:
||\displaystyle \theta_{c} = \sin^{-1} \left(\frac {n_{2}}{n_{1}}\right)||
where
|\theta_{c}| represents the critical angle
|n_{1}| represents the index of refraction of the medium containing the incident ray
|n_{2}| represents the index of refraction of the medium containing the refracted ray
It's important to remember that if the angle of incidence is equal to the critical angle, then the angle of refraction will be 90°, so there total internal reflection will not occur, since it is still being refracted. The incident angle must be greater than the critical angle for this phenomenon to occur.
The following illustration shows the different outcomes of light as it passes from a more refractive medium to a less refractive one, depending on the angle of incidence.
To identify the nature of an unknown substance, we decide to measure its critical angle and determine its refractive index. If we measure a critical angle of |56.4^{\circ}| when the ray passes from the unknown medium to air, what is the index of refraction of this unknown material?
The following information is available to help solve this problem:
||\begin{align}n_{1} &= ? &n_{2} &= 1.00\\
\theta_{c} &= 56.4^{\circ} \end{align}||
Using the critical angle formula, we can find the second medium's index of refraction:
||\begin{align} \sin \theta_{c} = \frac {n_{2}}{n_{1}} \quad \Rightarrow \quad
n_{1} &= \frac {n_{2}}{\sin \theta_{c}} \\
&= \frac {1.00}{\sin 56.4^{\circ}}\\
&\cong 1.2 \end{align}||
Total internal reflection is used, among other things, in the design of optical fibers. These fibers are notably used in telecommunications networks, such as those providing high-speed Internet access. Optic fibers consist of a glass or plastic filament, the core, with a higher refractive index than the cladding. When information is sent through it, it strikes the walls of the fiber, and undergoes total internal reflection.