Une réflexion totale interne survient lorsque l’angle du rayon réfracté dépasse |\small \text {90}^{\circ}|.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>À ce moment, le rayon incident ne peut plus pénétrer à l’intérieur du deuxième milieu et, par conséquent, le rayon subira une réflexion sur la surface séparant les deux milieux, et ce, selon <a href="/fr/eleves/bv/physique/la-geometrie-et-la-loi-de-la-reflexion-p1075">les lois de la réflexion</a>.</p>
</body></html>
Deux conditions doivent être réunies pour qu'une réflexion totale interne puisse se produire.
L’indice de réfraction du milieu incident doit être plus grand que celui du milieu réfracté (|\small n_{1} > n_{2}|).
L’angle d’incidence doit être supérieur à l’angle critique (|\small \theta_{i} > \theta_{c}|).
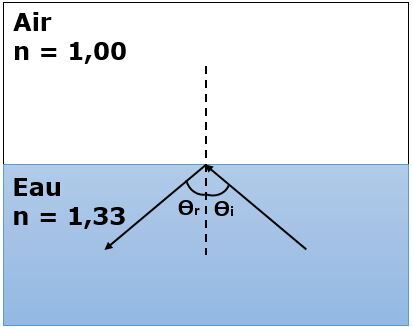
Dans l'exemple ci-dessous, le rayon incident passe dans l'eau et se dirige vers l'air. La première condition de la réflexion totale interne est donc respectée, puisque l'indice de réfraction du premier milieu, soit l'eau, est plus élevé que celui du deuxième milieu, soit l'air. Si l'angle d'incidence est plus grand que l'angle critique, le rayon incident se réfléchira alors comme s'il frappait la surface d'un miroir.
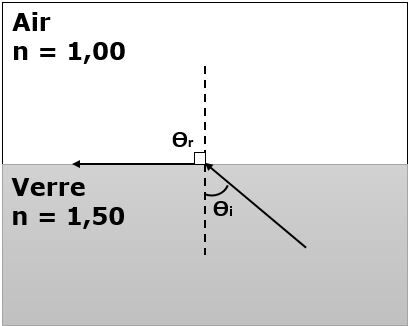
L’angle critique est l’angle incident avec lequel le rayon est réfracté à |\small \text {90}^{\circ}| dans le milieu de réfraction.
L'angle critique peut être observé dans l'image ci-dessous. Dans cette situation, l'angle d'incidence est égal à l'angle critique.
Il est possible d’utiliser la loi de Snell-Descartes pour en déduire l’équation suivante permettant de déterminer mathématiquement l’angle critique. Sachant que l'angle de réfraction est |\small \text {90}^{\circ}|, il est possible d'isoler la variable inconnue, soit l'angle d'incidence (qui équivaut à l'angle critique):
||\begin{align} n_{1}\times \sin \theta_{i} = n_{2}\times \sin\theta_{r} \quad \Rightarrow \quad n_{1}\times \sin \theta_{c} &= n_{2}\times \sin 90^{\circ} \\
n_{1}\times \sin \theta_{c} &= n_{2}\times 1 \\
\sin \theta_{c} &= \frac {n_{2}}{n_{1}} \end{align}||
La formule pour calculer l'angle critique est:
||\displaystyle \theta_{c} = \sin^{-1} \left(\frac {n_{2}}{n_{1}}\right)||
où
|\theta_{c}| représente l'angle critique
|n_{1}| : indice de réfraction du milieu contenant le rayon incident
|n_{2}| : indice de réfraction du milieu contenant le rayon réfracté
Il est important de se rappeler que si l’angle incident est égal à l’angle critique, alors l’angle de réfraction sera de 90° et donc, il n’y aura pas de réflexion totale interne, puisqu'une réfraction pourra se produire. L’angle incident doit être supérieur à l’angle critique pour qu’ait lieu ce phénomène.
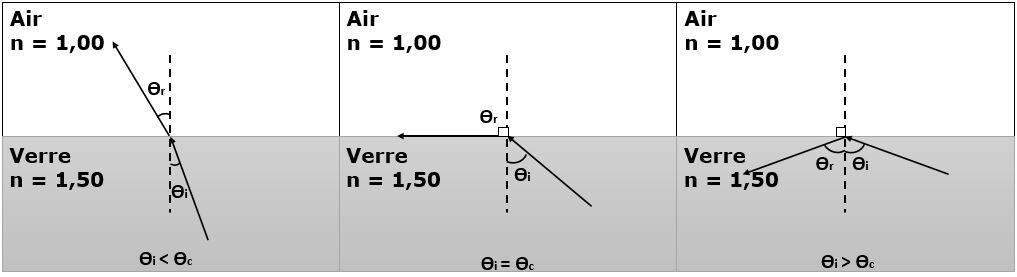
L'illustration ci-dessous démontre ce qui peut se produire avec la lumière lorsqu'elle passe d'un milieu plus réfringent vers un milieu moins réfringent selon l'angle d'incidence.
Afin d’identifier la nature d’une substance inconnue, on décide de mesurer son angle critique et de déterminer son indice de réfraction. Si on mesure un angle critique de |\small 56,4^{\circ}| lorsque le rayon passe du milieu inconnu à l'air, quel est l’indice de réfraction de ce matériau inconnu?
Les informations connues pour la résolution de ce problème sont les suivantes:
||\begin{align}n_{1} &= ? &n_{2} &= 1,00\\
\theta_{c} &= 56,4^{\circ} \end{align}||
En utilisant la formule de l'angle critique, il est possible de trouver l'indice de réfraction du deuxième milieu:
||\begin{align} \sin \theta_{c} = \frac {n_{2}}{n_{1}} \quad \Rightarrow \quad
n_{1} &= \frac {n_{2}}{\sin \theta_{c}} \\
&= \frac {1,00}{\sin 56,4^{\circ}}\\
&\cong 1,2 \end{align}||
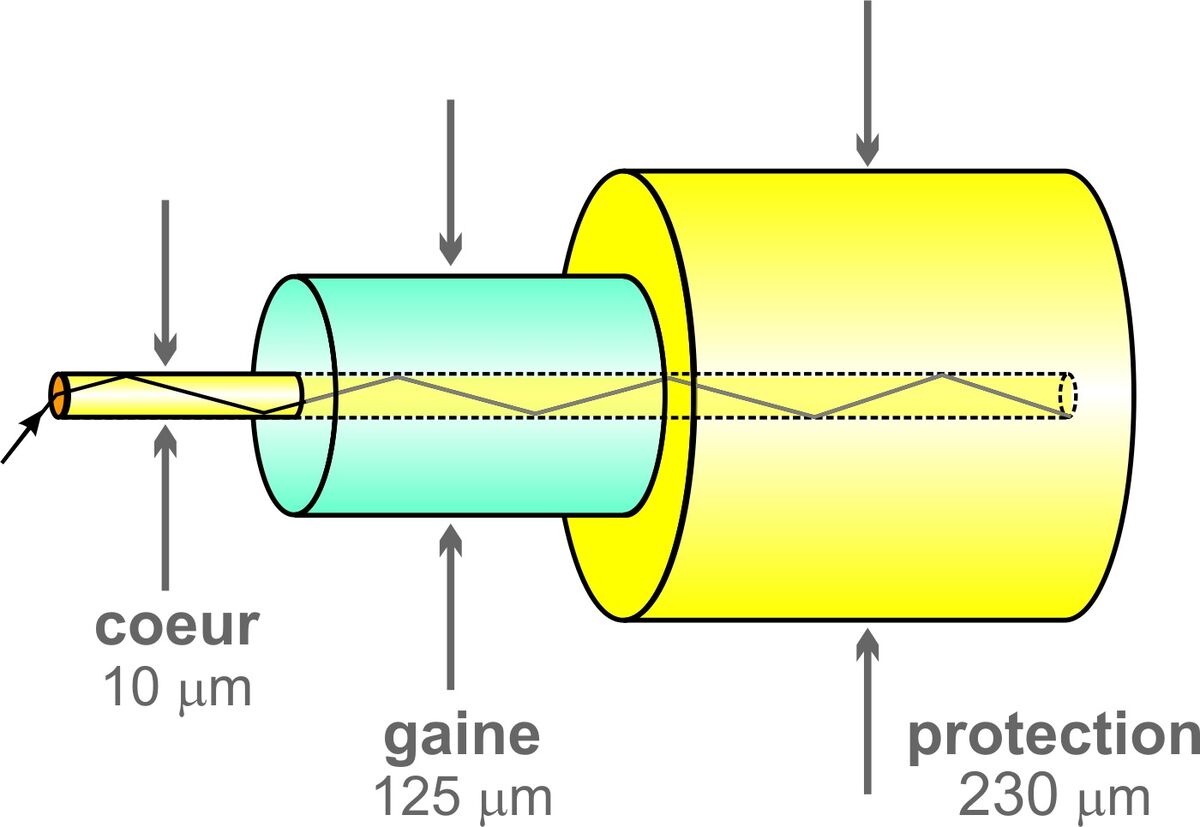
La réflexion totale interne est utilisée, entre autres, dans la conception des fibres optiques. Ces fibres sont notamment utilisées dans les réseaux de télécommunication, comme ceux qui permettent d'accéder à Internet en haute vitesse. La fibre optique est constituée d'un filament de verre ou de plastique, le coeur, ayant un indice de réfraction plus élevé que la gaine. Lorsqu'on y envoie de l'information, celle-ci frappe les parois de la fibre en subissant de la réflexion totale interne.