A vector, usually denoted |\overrightarrow u|, is a mathematical object that has both a magnitude and an orientation (i.e. a direction and a sense).
As its name suggests, a vector is in fact a straight line with a starting point and an arrow to indicate its end point and direction.
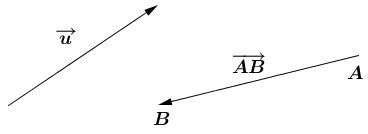
The vector on the left |(\overrightarrow {u})| corresponds to the traditional way of representing a vector. The vector on the right shows a vector originating at point A and travelling to point B. The notation |\overrightarrow {AB}| can be used to refer to this.
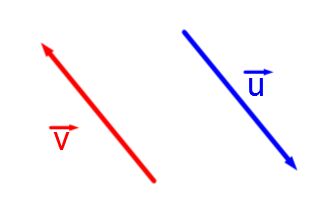
The definition of a vector deals not only with the magnitude of a vector, but also with its orientation. This orientation includes the direction (the straight line supporting the vector) and the sense (the arrow) of the vector. In order to distinguish between these concepts, it is best to compare vectors together.
In physics, vectors are used to represent distance travelled or forces. They can be used to determine the total distance travelled by an object or to calculate the resultant force exerted on an object. To do this, the vectors have to be added together, i.e. all the distance travelled (or all the forces) have to be added together to find the size and orientation of a single vector that would represent all these vectors.
Vectors are also used in mathematics. However, the approach and concepts are slightly different.
There are two methods for calculating the sum of an addition of vectors. These methods are presented in the following two sheets.