Lorsqu'une substance acide est mise en solution aqueuse, la constante d'équilibre prend une forme particulière. Les scientifiques ont donc élaboré une variante de la constante d'équilibre à appliquer dans cette situation : la constante d'acidité. Toutefois, une réaction à l'équilibre ne peut survenir qu'en cas de dissociation d'un acide faible. En effet, les acides forts se dissocient entièrement en solution ce qui constitue une réaction complète et donc irréversible.
La force d'un électrolyte, qu'il soit acide ou basique, correspond au pourcentage de dissociation de la substance en ions lorsque mise en solution.
Un électrolyte fort est un soluté qui se dissocie complètement dans l'eau.
Un électrolyte faible est un soluté qui ne se dissocie pas complètement dans l'eau.
Comme le stipulent les théories d'Arrhenius et de BrØnsted-Lowry, les acides et les bases sont des substances qui libèrent des ions lorsqu'ils sont en solution aqueuse. Ce sont donc des électrolytes. Toutefois, ils ne subissent pas tous la dissociation électrolytique au même degré. C'est ce qui explique la présence d'électrolytes forts et d'électrolytes faibles. Avant d'étudier la constante d'acidité, il est important de distinguer ces substances en fonction de leur force, puisque seuls les électrolytes faibles pourront être à l'état d'équilibre chimique.
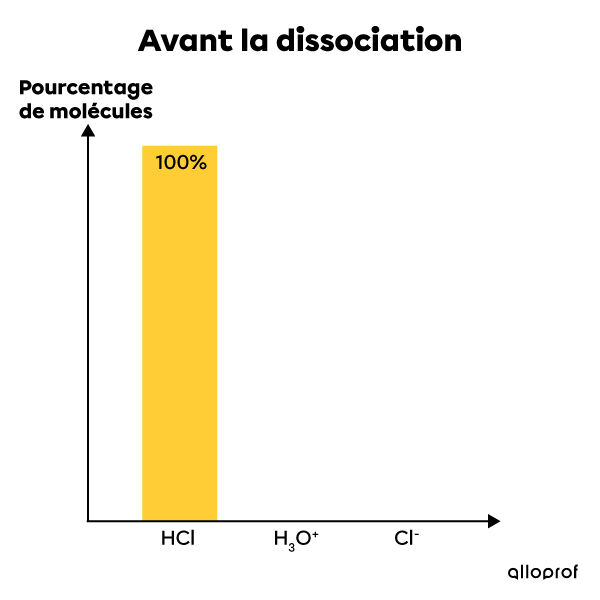
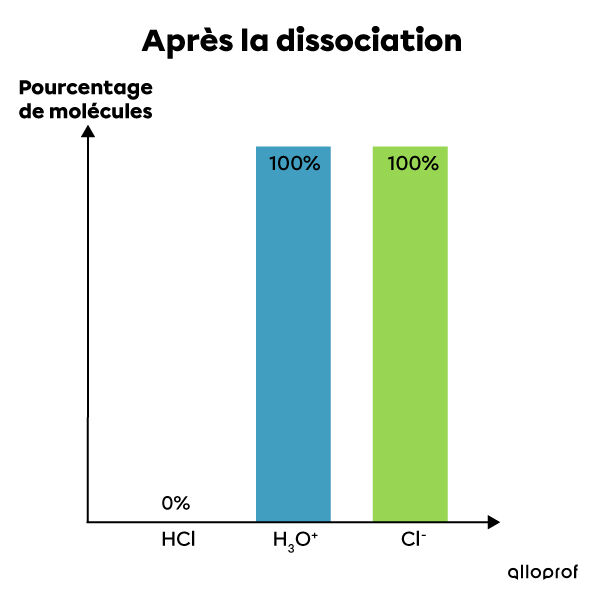
L'acide chlorhydrique est un électrolyte fort. Lorsqu'il est mis en solution dans l'eau, il se dissocie complètement en ions. Ainsi, 100% de ses molécules se dissocient et forment des ions |H^{+}| et |Cl^{-}|. La solution contient alors le même pourcentage d'ions après la dissociation qu'il y avait de molécules d'acide avant la dissociation. Il s'agit donc d'une réaction complète qui ne peut être à l'équilibre. On écrit cette réaction chimique de la façon suivante:|HCl_{(aq)} + H_{2}O_{(l)} \rightarrow H_{3}O^{+}_{(aq)} + Cl^{-}_{(aq)}|
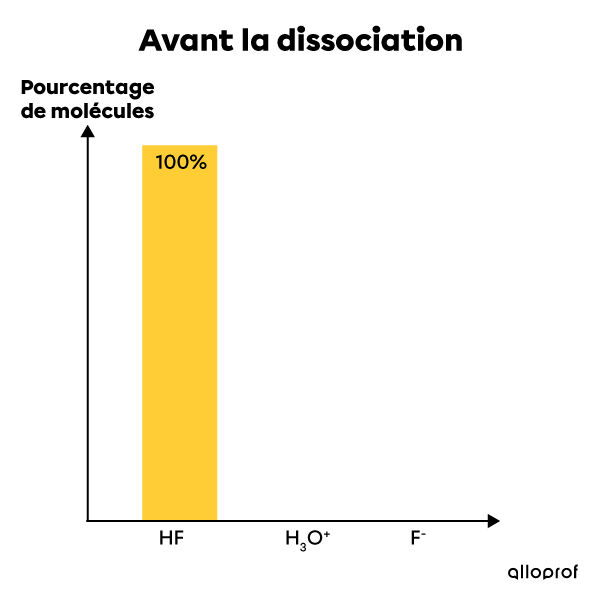
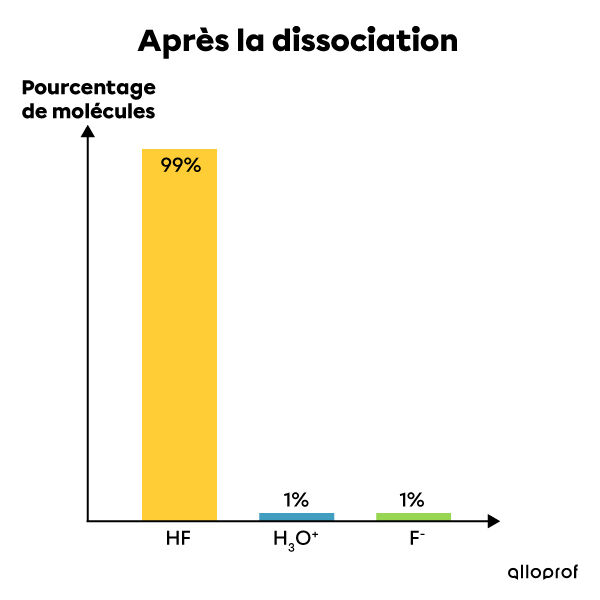
L'acide fluorhydrique est un électrolyte faible. Lorsqu'il est mis en solution dans l'eau, seule une partie de ses molécules se dissocie en ions. Ainsi, la plupart de ses molécules restent entières après la dissolution tandis qu'un très faible pourcentage de ses molécules se dissocient et forment des ions |H^{+}| et |F^{-}|. La solution contient alors à la fois des réactifs (la molécule entière) et des produits (les ions en solution). Il s'agit donc d'une réaction incomplète et réversible qui est à l'équilibre. On écrit cette réaction chimique de la façon suivante:|HF_{(aq)} + H_{2}O_{(l)} \rightleftharpoons H_{3}O^{+}_{(aq)} + F^{-}_{(aq)}|
Seuls les électrolytes faibles peuvent être à l'état d'équilibre.
On peut calculer le pourcentage de molécules qui se dissocient dans un solvant à l'aide de la formule du pourcentage d'ionisation :
|\text {Pourcentage d'ionisation} = \displaystyle \frac{[H_{3}O^{+}]}{[HA]}\times 100|
où
|[H_{3}O^{+}]| représente la concentration des ions |[H_{3}O^{+}]| à l'équilibre |\small (\text {mol/L})|
|[HA]| représente la concentration de l'acide avant la dissolution |\small (\text {mol/L})|
En plus de nous permettre de connaître le pourcentage d'ionisation de l'électrolyte, cette formule permet de déterminer la concentration des ions en situation d'équilibre. On peut alors calculer la constante d'acidité.
La plupart des acides sont des acides faibles qui peuvent atteindre l'état d'équilibre en solution aqueuse. À l'équilibre, les molécules de l'acide se dissocient à la même vitesse que les ions formés se recombinent pour reformer les molécules de l'acide. On peut généraliser cette réaction de la façon suivante:
|HA_{(aq)} + H_{2}O_{(l)} \rightleftharpoons H_{3}O^{+}_{(aq)} + A^{-}_{(aq)}|
ou encore:
|HA_{(aq)} \rightleftharpoons H^{+}_{(aq)} + A^{-}_{(aq)}|
La constante d'équilibre qui est associée à l'ionisation d'un acide, nommée «constante d'acidité», est alors exprimée de la façon suivante:
|K_{a}=\displaystyle \frac{[H^{+}][A^{-}]}{[HA]}|
où |K_{a}| représente la constante d'acidité
|[H^{+}]| représente la concentration en ions hydronium dans l'eau |\small (\text {mol/L})|
|[A^{-}]| représente la concentration de la base conjuguée |\small (\text {mol/L})|
|[HA]| représente la concentration de l'acide non dissocié |\small (\text {mol/L})|
La constante d'acidité |K_{a}| est une variante de la constante d'équilibre. La concentration de l'eau n'y apparaît pas puisque l'eau est en phase liquide. La constante d'acidité permet un classement des acides en fonction de leur force. En effet, plus la constante est petite, plus un acide est faible.
1. Expression de la constante d'acidité
|[C_{4}H_{4}N_{2}O_{3}] \rightleftharpoons [H^{+}] + [C_{4}H_{3}N_{2}O_{3}^{-}]|
|K_{a} = \displaystyle \frac{[H^{+}][C_{4}H_{3}N_{2}O_{3}^{-}]}{[C_{4}H_{4}N_{2}O_{3}]}|
2. Transformation du pH en concentration molaire
|[H^{+}] = 10^{-pH}|
|[H^{+}] = 10^{-2,5}|
|[H^{+}] = 3,16\times 10^{-3} \text { mol/L}|
3. Tableau des concentrations à l'équilibre
| | |C_4H_4N_2O_3| | |\rightarrow| | |H^+| | |+| | |C_4H_3N_2O_3^-| |
| [Initiale] | |\color{red}{0,10}| | |\huge\Rightarrow| | |\color{red}{0}| | |\huge +| | |\color{red}{0}| |
| [Variation] | |(-3,16\times10^{-3})| | |(+3,16\times10^{-3})| | |(+3,16\times10^{-3})| | ||
| [Équilibre] | |9,68\times10^{-2}| | |\color{red}{3,16\times10^{-3}}| | |3,16\times10^{-3}| |
|K_{a}=\displaystyle \frac{[3,16\times 10^{-3}][3,16\times 10^{-3}]}{[9,68\times 10^{-2}]}|
|K_{a}=1,03\times 10^{-4}|
5. Calcul du pourcentage d'ionisation
|\text {Pourcentage d'ionisation} = \displaystyle \frac{[3,16\times 10^{-3}]}{[0,10]}\times 100|
|\text {Pourcentage d'ionisation} = 3,16| %
1. Expression de la constante d'acidité
|[HCOOH] \rightleftharpoons [H^{+}] + [HCOO^{-}]|
|K_{a} = \displaystyle \frac{[H^{+}][HCOO^{-}]}{[HCOOH]}|
2. Tableau des concentrations à l'équilibre
| | |HCOOH| | |\rightarrow| | |H^+| | |+| | |HCOO^-| |
| [Initiale] | |\color{red}{0,10}| | |\huge\Rightarrow| | |\color{red}{0}| | |\huge +| | |\color{red}{0}| |
| [Variation] | |(-x)| | |(+x)| | |(+x)| | ||
| [Équilibre] | |0,10 - x| | |x| | |x| |
3. Calcul de la concentration en ions |H^{+}|
|1,77\times 10^{-4} = \displaystyle \frac{[x][x]}{[0,10 - x]}|
Il s'agit d'une équation du second degré dans laquelle on devra isoler le x. La seule réponse possible sera:
|[H^{+}]| = |4,1\times 10^{-3}\text { mol/L}|
4. Calcul du pH
|pH = -\log[H^{+}]|
|pH = -\log[4,1\times 10^{-3}]|
|pH = 2,39|
Les outils suivants peuvent être utiles dans les calculs de |K_{a}|:
• La constante d'acidité de quelques substances acides