Calculer l’aire | Primaire

Certaines figures peuvent avoir des demi-carrés. Deux demi-carrés forment un carré-unité.

Pour calculer l’aire d’une figure, je dois suivre les étapes suivantes :

1. Je vérifie s’il y a des demi-carrés et je les assemble pour former des carrés-unités.

2. Je compte le nombre de carrés-unités total, incluant ceux formés avec les demi-carrés.

Quelle est l’aire de cette figure?

Je vérifie s’il y a des demi-carrés et je les assemble pour former des carrés-unités. Je forme 2 carrés-unités avec les 4 demi-carrés.
Je compte le nombre de carrés-unités total incluant ceux formés avec les demi-carrés.

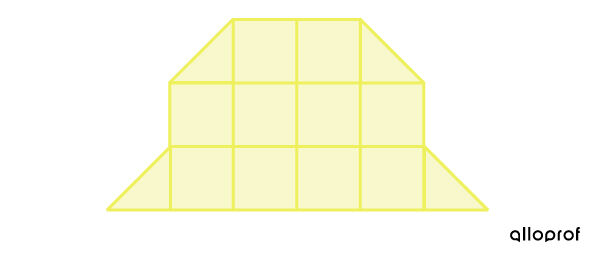
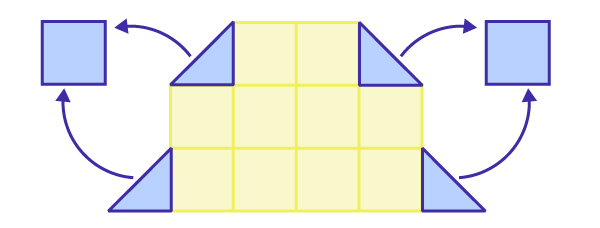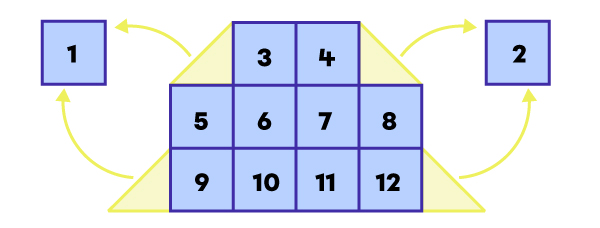L’aire de cette figure est de 12 carrés-unités.

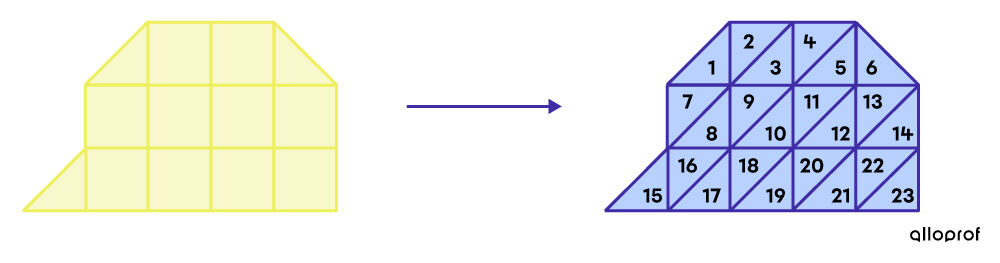
Lorsque la figure présente un nombre impair de demi-carrés, tu dois calculer l’aire de la figure en demi-carrés. Pour ce faire, tu dois diviser chaque carré-unité en deux demi-carrés.

Exemple :

L’aire de cette figure est de 23 demi-carrés.

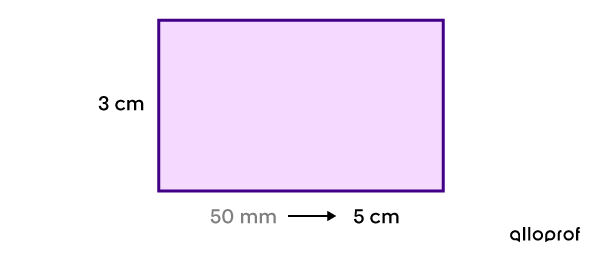
Lorsque tu calcules l’aire, tu dois t'assurer qu'une seule unité de mesure est utilisée. Si ce n'est pas le cas, tu dois faire une ou des conversions avant de faire le calcul.

Pour savoir comment faire, tu peux lire la fiche La conversion des unités de mesure de longueur.

Exemple :

Je choisis de convertir 50 mm en cm pour avoir une seule unité de mesure.

Pour calculer l’aire d’une figure, je dois suivre les étapes suivantes :

1. Je vérifie que les mesures sont données dans la même unité. Si ce n'est pas le cas, je dois les convertir. 

2. Je multiplie la longueur et la largeur ensemble pour trouver l’aire.

Quelle est l’aire de la figure en décimètres carrés (dm²)?

Je vérifie que les mesures sont données dans la même unité. Si ce n'est pas le cas, je dois les convertir.  Pour savoir comment faire, je peux lire la fiche La conversion des unités de mesure de longueur. Puisque je dois trouver l’aire de la figure en dm², je convertis 10 m en dm.
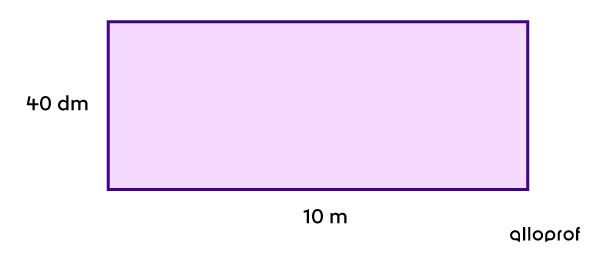
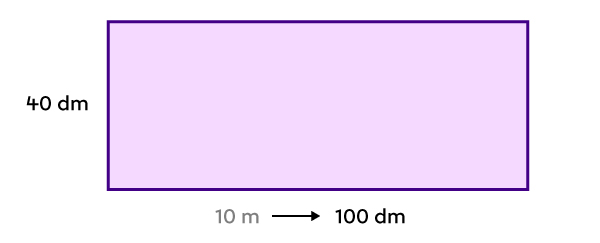Je multiplie la longueur et la largeur ensemble pour trouver l’aire.	100 dm × 40 dm = 4 000 dm²

L’aire de la figure est de 4 000 dm².

Pour calculer l’aire d’une figure complexe, je dois suivre les étapes suivantes :

1. Je vérifie si les mesures sont données dans la même unité. Si ce n'est pas le cas, je dois les convertir. 

2. Je divise la figure en carrés ou en rectangles.

3. Je calcule l'aire de chaque section en multipliant ensemble la longueur et la largeur.

4. J’additionne l’aire de toutes les sections pour obtenir l’aire totale.

Quelle est l’aire de la figure en mètres carrés (m²)?

Je vérifie si les mesures sont données dans la même unité. Si ce n'est pas le cas, je dois les convertir.  Puisque je dois trouver l’aire de la figure en m², je convertis 20 dm en m.
Je divise la figure en carrés ou en rectangles. J’obtiens 2 rectangles : le A et le B.
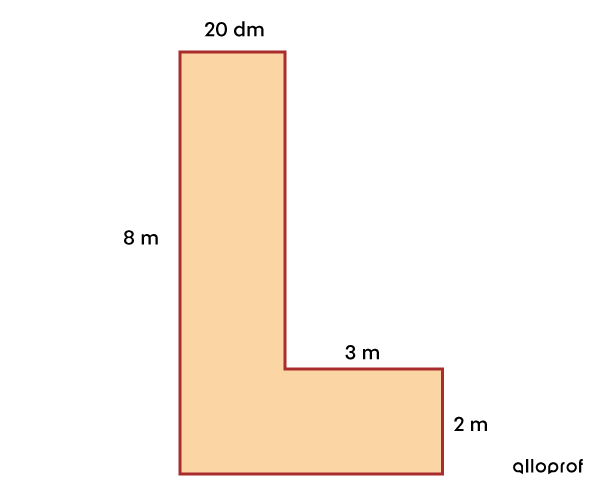
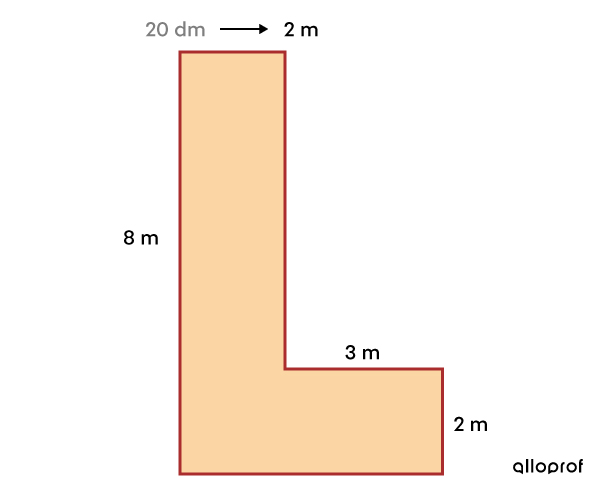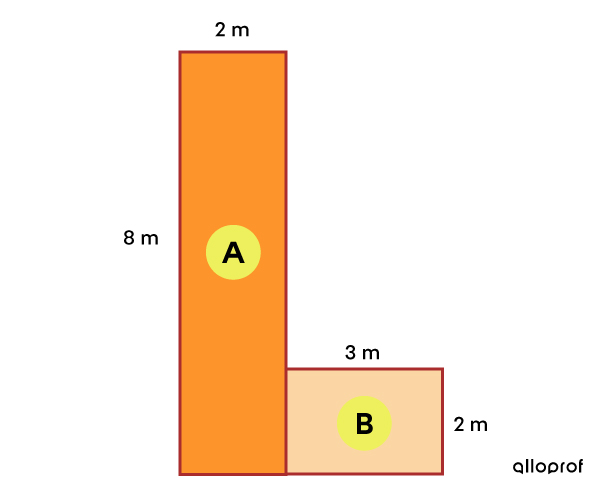Je calcule l'aire de chaque section en multipliant ensemble la longueur et la largeur. La figure A a une longueur de 8 m et une largeur de 2 m. La figure B a une longueur de 3 m et une largeur de 2 m.	A : 8 m × 2 m = 16 m² B : 3 m × 2 m = 6 m²
J’additionne l’aire de toutes les sections pour obtenir l’aire totale.	16 m² + 6 m² = 22 m²

L’aire de la figure est de 22 m².