Par définition, les rapports trigonométriques sont applicables seulement dans les triangles rectangles. S'il n'y a aucun angle droit dans le triangle avec lequel on travaille, on peut se servir des propriétés des différents segments afin de créer un tel angle. En procédant adéquatement, on pourra trouver les mesures manquantes qui permettront de calculer l'aire du triangle avec lequel on travaille.
Contrairement aux rapports trigonométriques, la formule trigonométrique ne sert pas à trouver une mesure de côté, mais plutôt à calculer l'aire d'un triangle.
||A_\text{triangle} = \displaystyle \frac{\color{green}{a} \times \color{blue}{b} \times \sin \color{red}{C}}{2}||
où
|\color{green}{a} \ \text{et} \ \color{blue}{b}| sont des mesures de côtés;
|\color{red}{C}| est la mesure de l'angle formé par ces côtés tel qu'illustré ci-dessous.
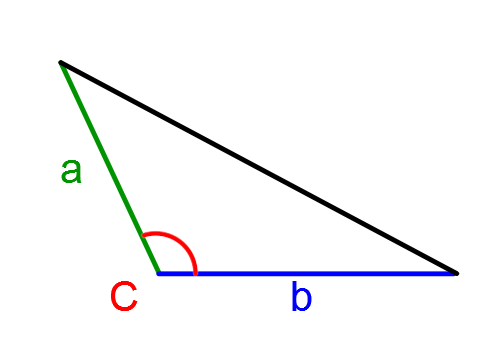
Pour démontrer la justesse de cette formule, on utilise les rapports trigonométriques.
Pour démontrer la formule trigonométrique, on utilise le triangle suivant:

Dans ce cas, on peut déterminer que
||A_\text{triangle} = \displaystyle \frac{\color{red}{a} \times h }{2}||
Selon le moyen triangle rectangle de gauche, on peut déterminer que
||\begin{align} \sin C &= \frac{h}{\color{green}{b}} \\
\Rightarrow \color{green}{b} \times \sin C &= h \end{align}||
Par substitution de la variable |h|, on obtient
||\begin{align} A_\text{triangle} &= \frac{\color{red}{a} \times h}{2}\\
&= \frac{ \color{red}{a} \times \color{green}{b} \times \sin C}{2}\end{align}||
Malgré le fait qu'on analyse les cas de triangles non rectangles, on peut utiliser les propriétés des autres types de triangles (isocèle et rectangle) et la relation de Pythagore.
Par ailleurs, quand ces informations sont directement disponibles, la démarche à suivre et les calculs diffèrent quelque peu.
Ayant une terre agricole trop grande, un agriculteur décide de se départir d'une portion de sa terre.
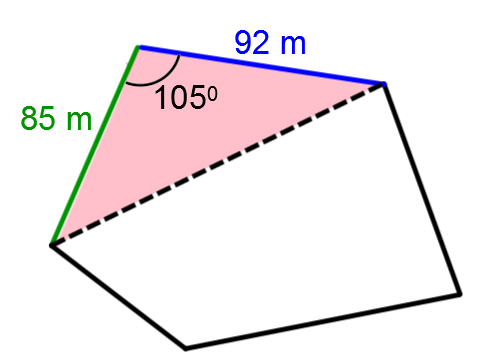
Quel prix devrait-il demander pour cette portion de terrain si les lots de ce genre se vendent généralement 15 $ / m2 ?
1) Identifier les mesures essentielles
Toutes les mesures essentielles à l'application de la formule trigonométrique sont données:
||\begin{align} \color{green}{a} &= \color{green}{ 85 \ \text{m}}\\
\color{blue}{b} &= \color{blue}{92 \ \text{m}}\\
\text{m} \angle C &= 105^\circ \end{align}||
2) Appliquer la formule trigonométrique
||\begin{align}\color{red}{A_\text{triangle}} &= \frac{\color{green}{a} \times \color{blue}{b} \times \sin C}{2} \\
&= \frac{\color{green}{85} \times \color{blue}{92} \times \sin 105^\circ}{2}\\
&\approx 3 \ 776,77 \ \text{m}^2 \end{align}||
3) Interpréter la réponse
Ainsi, le prix de vente | = 15 \times 3 \ 776,77 = 56 \ 651,55 \$|.
En résumé, il est possible d'appliquer la formule trigonométrique aussitôt que l'on connait les mesures de l'angle et des côtés qui le forment.
L'idée derrière cette technique est de former des triangles rectangles afin de permettre l'utilisation des rapports trigonométriques. Avec ces rapports, il devient plus facile de trouver les mesures manquantes pour calculer l'aire du triangle non rectangle.
Hauteur à l'intérieur du triangle
Pour arriver à calculer l'aire du triangle suivant, il est préférable de tracer une hauteur qui est issue du sommet C:
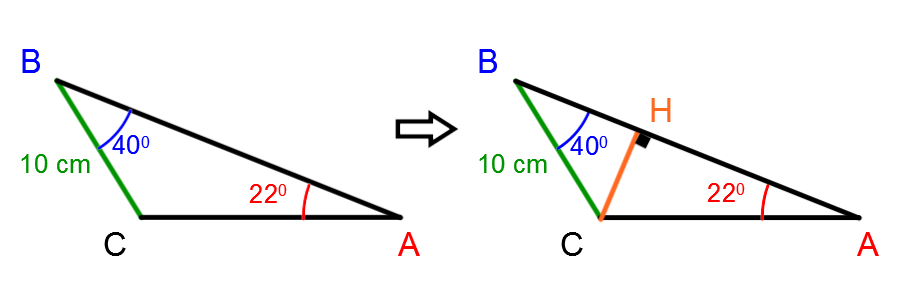
Ainsi, on peut trouver les mesures manquantes en utilisant les rapports trigonométriques suivants:
||\begin{align} &1. &\sin 40^\circ &= \frac{\color{orange}{m \overline{CH}}}{\color{green}{m \overline{BC}}}\\
&&\Rightarrow \color{orange}{m \overline{CH}} &= \sin 40^\circ \times \color{green}{m \overline{BC}}\\\\&2.& \cos 40^\circ &= \frac{m \overline{BH}}{\color{green}{m \overline{BC}}} \\
&&\Rightarrow m \overline{BH} &= \cos 40^\circ \times \color{green}{m \overline{BC}}\\\\
&3.& \tan \color{red}{22^\circ} &= \frac{\color{orange}{m \overline {CH}}}{m \overline{AH}}\\
&&\Rightarrow m \overline{AH} &= \displaystyle \frac{\color{orange}{m \overline{CH}}}{\tan \color{red}{22^\circ}}\end{align}||
4. En considérant |\overline{AB}| comme la base et |\color{orange}{\overline{CH}}| comme la hauteur du triangle, on peut calculer l'aire
||\begin{align} \Delta ABC &= \frac{(m \overline{AH} + m \overline {BH}) \times \color{orange}{m \overline{CH}}}{2}\\
&= \frac{m\overline{AB} \times \color{orange}{m \overline{CH}}}{2}\end{align}||
Par ailleurs, le même genre de démarche peut s'appliquer lorsque la hauteur du triangle est tracée à l'extérieur du triangle.
Hauteur à l'extérieur du triangle
Pour arriver à calculer l'aire du triangle suivant, il est préférable de tracer une hauteur qui est issue du sommet B:
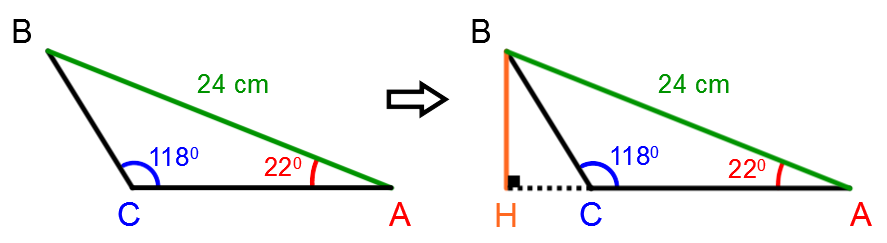
Ainsi, on peut trouver les mesures manquantes en utilisant les rapports trigonométriques suivants:
||\begin{align} &1.&m \angle BCH &= 180^\circ - \color{blue}{m \angle BCA} \\
&&&= 180^\circ - \color{blue}{118^\circ}\\
&&&= 62^\circ\\\\
&2.& \sin \color{red}{22^\circ} &= \frac{\color{orange}{m \overline{BH}}}{\color{green}{m \overline{BA}}}\\
&& \Rightarrow \color{orange}{m \overline{BH}} &= \sin \color{red}{22^\circ} \times \color{green}{m \overline{BC}}\\\\
&3.& \color{red}{m \overline{AC}} &= m \overline {AH} - m \overline{CH}\end{align}||
Selon|\Delta BCH|,
||\begin{align}\tan 62^\circ &= \frac{\color{orange}{m \overline {BH}}}{m \overline{CH}} \\ \Rightarrow m \overline {CH}
&= \frac{\color{orange}{m \overline{BH}}}{\tan 62^\circ}\end{align}||
Selon |\Delta ABH|,
||\begin{align} \cos \color{red}{22^\circ} &= \frac{m \overline {AH}}{\color{green}{m \overline {AB}}} \\
m \overline {AH} &= \cos \color{red}{22^\circ} \times \color{green}{m \overline {AB}}\end{align}||
4. En considérant |\color{red}{\overline {AC}}| comme la base et |\color{orange}{\overline{BH}}| comme la hauteur, on peut calculer l'aire du triangle ABC,
||\begin{align} A_\Delta &= \frac{(m \overline {AH} - m \overline{CH}) \times \color{orange}{m \overline {BH}}}{2} \\
&= \frac{\color{red}{m \overline {AC}} \times \color{orange}{m \overline{BH}}}{2}\end{align}||
Fait à noter, il est important que le triangle rectangle formé avec le traçage de la hauteur contienne au moins une mesure d'angle (autre que l'angle droit) et au moins une mesure de côté.
Dans le cas des triangles isocèles, la formule trigonométrique et les rapports trigonométriques sont utilisés. Dans le cas des rapports, ils sont essentiels pour trouver les mesures de côtés ou d'angle manquantes.
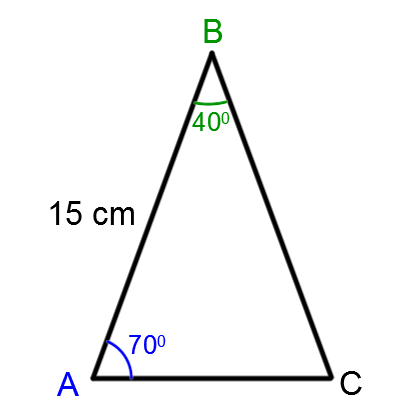
1) Tracer une hauteur appropriée
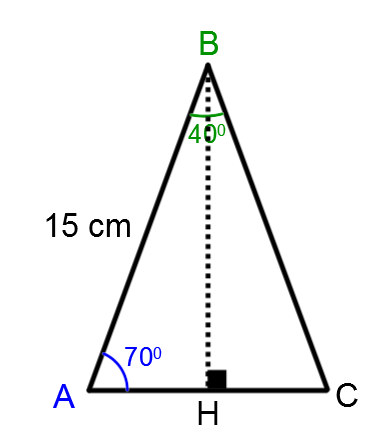
Ainsi
||\begin{align}\text{m} \angle C &= 180^\circ - \color{blue}{70^\circ} - \color{green}{40^\circ} \\
&= 70^\circ\\
\Rightarrow \angle C &= \color{blue}{\text{m} \angle A} \\
&= 70^\circ\end{align}||
Alors, le |\Delta ABC | est isocèle.
2) Utiliser les rapports trigonométriques
Avec la hauteur, on peut utiliser le rapport trigonométrique associé à la cathète |\overline {AH}| du |\Delta AHB|:
||\begin{align} \cos \color{blue}{70^\circ} &= \frac{\text{m} \overline{AH}}{15}\\
\Rightarrow m \overline{AH} &= \cos \color{blue}{70^\circ} \times 15\\
&\approx 5,12 \ \text{cm}\\\\
\sin \color{blue}{70^\circ} &= \frac{\color{orange}{m \overline{BH}}}{15} \\
\Rightarrow \color{orange}{m \overline {BH}} &= \sin \color{blue}{70^\circ} \times 15\\
&\approx \color{orange}{14,1 \ \text{cm}}\end{align}||
Par ailleurs,
||\begin{align} m \angle BCA &= 180^\circ - \color{blue}{70^\circ} - \color{green}{40^\circ} \\
&= 70^\circ\end{align}||
Puisqu'il s'agit d'un triangle isocèle,
||\begin{align} \color{red}{\text{m} \overline {AC}} &= 2 \times \text{m} \overline {AH} \\
&= 2 \times 5,12 \\
&= \color{red}{10,24\ \text{cm}}\end{align}||
3) Appliquer la formule
||\begin{align} A_\text{triangle}&= \frac{\color{red}{\text{base}} \times \color{orange}{\text{hauteur}}}{2}\\
&= \frac{\color{red}{10,24} \times \color{orange}{14,1}}{2}\\
&\approx 72,19 \ \text{cm}^2\end{align}||
4) Interpréter la réponse
L'aire de ce triangle est d'environ 72,19 cm2.
Dans les cas plus complexes, on ne retrouve que la mesure d'un seul côté, mais deux mesures d'angles différents. Pour arriver aux résultats recherchés, il faudra réinvestir une partie des démarches des exemples précédents en traçant des hauteurs.
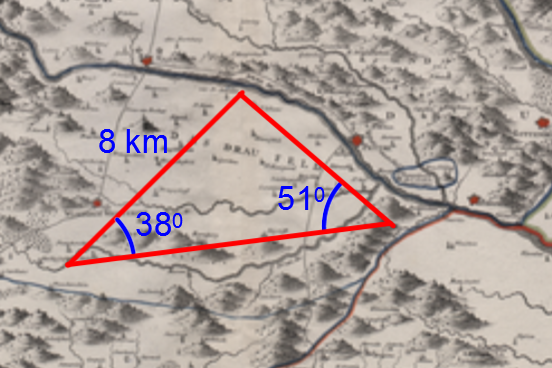
Pour accueillir tous les soldats et leur matériel, la superficie de cette nouvelle base doit être d'au moins |25 \ \text{km}^2|. Est-ce que le plan dessiné ci-dessus respecte cette condition?
1) Tracer une hauteur appropriée
Afin de former deux triangles rectangles, on trace la hauteur suivante:
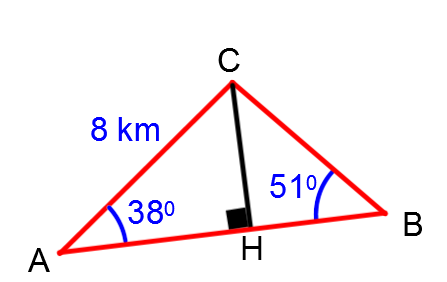
2) Utiliser les rapports trigonométriques
Pour calculer l'aire de ce triangle, il faut trouver |\color{blue}{\text{m} \overline {AB}}|.
||\begin{align}\sin 38^\circ &= \frac{\color{green}{\text{m} \overline {CH}}}{8 \ \text{km}} \\
\color{green}{\text{m} \overline {CH}} &\approx 4,5 \ \text{km}\\\\
\cos 38^\circ &= \frac{\text{m} \overline {AH}}{8 \ \text{km}} \\
\text{m} \overline {AH} &\approx 6,62 \ \text{km}\\\\
\tan 51^\circ &= \frac{\color{green}{\text{m} \overline {CH}}} {\text{m} \overline {BH}} \\
\tan 51^\circ &= \frac{4,5 \ \text{km}}{\text{m} \overline {BH}} \\
\text{m} \overline {BH} &\approx 4,36 \ \text{km}\\\\
\color{blue}{\text{m} \overline{AB}} &= \text{m} \overline {AH} + \text{m} \overline {HB} \\
&= 6,62 + 4,36 \\
&= \color{blue}{10,98 \ \text{km}}\end{align}||
3) Calculer l'aire
||\begin{align} A_\text{triangle} &= \frac{\color{blue}{\text{base}} \times \color{green}{\text{hauteur}}}{2}\\
&= \frac { \color{blue}{m \overline{AB}} \times \color{green}{m \overline{CH}}}{2}\\
&= \frac { \color{blue}{10,98} \times \color{green}{4,5}}{2}\\
&\approx 24,71 \ \text{km}^2\end{align}||
4) Interpréter la réponse
Les généraux devront retourner à leur planche à dessin puisque l'aire du triangle qu'ils ont tracé est plus petite que |25 \ \text{km}^2|.
Dans l’exemple précédent, il aurait été possible d’utiliser la loi des sinus pour déterminer |\color{blue}{\text{m} \overline {AB}}.|
Pour valider ta compréhension de la trigonométrie de façon interactive, consulte la MiniRécup suivante :
