By definition, trigonometric ratios are applicable only for right triangles. If no right angle exists in a triangle, the properties of different segments can be used to create one. The missing measurements can be found to calculate the area of any triangle.
Unlike trigonometric ratios, the trigonometric formula is not used to find a side measurement, but to calculate the area of a triangle.
||A_\text{triangle} = \displaystyle \frac{\color{green}{a} \times \color{blue}{b} \times \sin \color{red}{C}}{2}||
Where
|\color{green}{a} \ \text{and} \ \color{blue}{b}| are measurements of the sides.
|\color{red}{C}| is the measurement of the angle formed by the sides, as follows:
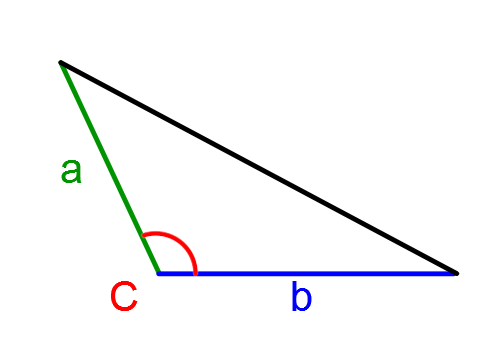
Demonstrating the formula using trigonometric ratios.
To demonstrate the trigonometric formula, use the following triangle:

In this case, the following can be determined:
||A_\text{triangle} = \displaystyle \frac{\color{red}{a} \times h }{2}||
According to the medium right-angle triangle on the left, the following can be determined:
||\begin{align} \sin C &= \frac{h}{\color{green}{b}} \\
\Rightarrow \color{green}{b} \times \sin C &= h \end{align}||
Substituting the variable |h| gives:
||\begin{align} A_\text{triangle} &= \frac{\color{red}{a} \times h}{2}\\
&= \frac{ \color{red}{a} \times \color{green}{b} \times \sin C}{2}\end{align}||
Despite the fact that we are studying non-right triangle situations, the properties of other types of triangles (isosceles and right) and the Pythagorean Theorem can be used.
However, when the information is available, the procedure and calculations differ slightly.
A farmer has too much agricultural land and decides to sell off a portion of it.
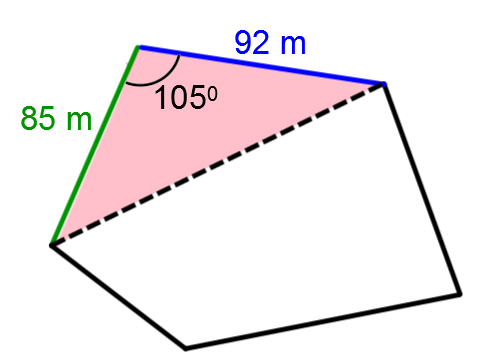
What price should he charge for the portion of land if the going price is $15 / m2?
-
Identify the essential measurements.
All the numbers essential for applying the trigonometric formula are given as follows:
||\begin{align} \color{green}{a} &= \color{green}{ 85 \ \text{m}}\\
\color{blue}{b} &= \color{blue}{92 \ \text{m}}\\
\text{m} \angle C &= 105^\circ \end{align}|| -
Apply the trigonometric formula.
||\begin{align}\color{red}{A_\text{triangle}} &= \frac{\color{green}{a} \times \color{blue}{b} \times \sin C}{2} \\
&= \frac{\color{green}{85} \times \color{blue}{92} \times \sin 105^\circ}{2}\\
&\approx 3 \ 776.77 \ \text{m}^2 \end{align}|| -
Interpret the answer.
The selling price is | = 15 \times 3776.77 = \$56\ 651.55.|
In summary, it is possible to apply the trigonometric formula when the measurements of an angle and the sides forming it are known.
The principle behind this method is to form right triangles to allow the use of trigonometric ratios. With these ratios, it is easier to find the missing measurements needed to calculate the area of a non-right triangle.
Height inside the triangle
To calculate the area of the following triangle, draw the height originating from vertex C:
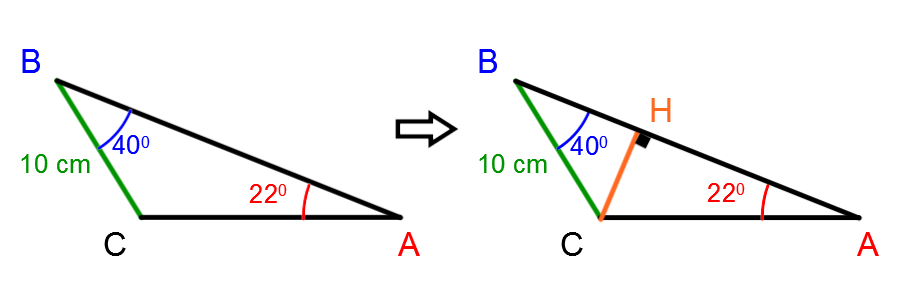
Thus, the missing measurements can be found using the following trigonometric ratios:
||\begin{align} &1. &\sin 40^\circ &= \frac{\color{orange}{m \overline{CH}}}{\color{green}{m \overline{BC}}}\\
&&\Rightarrow \color{orange}{m \overline{CH}} &= \sin 40^\circ \times \color{green}{m \overline{BC}}\\\\&2.& \cos 40^\circ &= \frac{m \overline{BH}}{\color{green}{m \overline{BC}}} \\
&&\Rightarrow m \overline{BH} &= \cos 40^\circ \times \color{green}{m \overline{BC}}\\\\
&3.& \tan \color{red}{22^\circ} &= \frac{\color{orange}{m \overline {CH}}}{m \overline{AH}}\\
&&\Rightarrow m \overline{AH} &= \displaystyle \frac{\color{orange}{m \overline{CH}}}{\tan \color{red}{22^\circ}}\end{align}||
4. Considering |\overline{AB}| as the base and |\color{orange}{\overline{CH}}| as the height of the triangle, the area can be calculated as follows:
||\begin{align} \Delta ABC &= \frac{(m \overline{AH} + m \overline {BH}) \times \color{orange}{m \overline{CH}}}{2}\\
&= \frac{m\overline{AB} \times \color{orange}{m \overline{CH}}}{2}\end{align}||
The same approach can be used when the height of the triangle is drawn outside the triangle.
The height outside the triangle
To calculate the area of the following triangle, draw the height originating from vertex B:
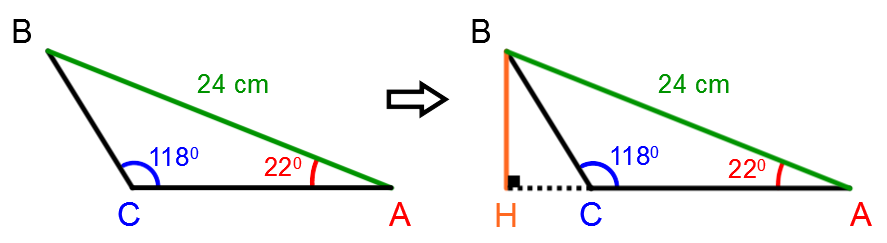
Thus, the missing measurements can be found using the following trigonometric ratios:
||\begin{align} &1.&m \angle BCH &= 180^\circ - \color{blue}{m \angle BCA} \\
&&&= 180^\circ - \color{blue}{118^\circ}\\
&&&= 62^\circ\\\\
&2.& \sin \color{red}{22^\circ} &= \frac{\color{orange}{m \overline{BH}}}{\color{green}{m \overline{BA}}}\\
&& \Rightarrow \color{orange}{m \overline{BH}} &= \sin \color{red}{22^\circ} \times \color{green}{m \overline{BC}}\\\\
&3.& \color{red}{m \overline{AC}} &= m \overline {AH} - m \overline{CH}\end{align}||
According to |\Delta BCH|,
||\begin{align}\tan 62^\circ &= \frac{\color{orange}{m \overline {BH}}}{m \overline{CH}} \\ \Rightarrow m \overline {CH}
&= \frac{\color{orange}{m \overline{BH}}}{\tan 62^\circ}\end{align}||
According to |\Delta ABH|,
||\begin{align} \cos \color{red}{22^\circ} &= \frac{m \overline {AH}}{\color{green}{m \overline {AB}}} \\
m \overline {AH} &= \cos \color{red}{22^\circ} \times \color{green}{m \overline {AB}}\end{align}||
4. Considering |\color{red}{\overline {AC}}| as the base and |\color{orange}{\overline{BH}}| as the height, we can calculate the area of triangle ABC,
||\begin{align} A_\Delta &= \frac{(m \overline {AH} - m \overline{CH}) \times \color{orange}{m \overline {BH}}}{2} \\
&= \frac{\color{red}{m \overline {AC}} \times \color{orange}{m \overline{BH}}}{2}\end{align}||
Note: It is important that the right-angled triangle formed by drawing the height contains at least one angle measurement (other than the right angle) and at least one side measurement.
For isosceles triangles, the trigonometric formula and trigonometric ratios are used. In the case of the ratios, they are essential for finding missing side or angle measurements.
What is the area of the following triangle?
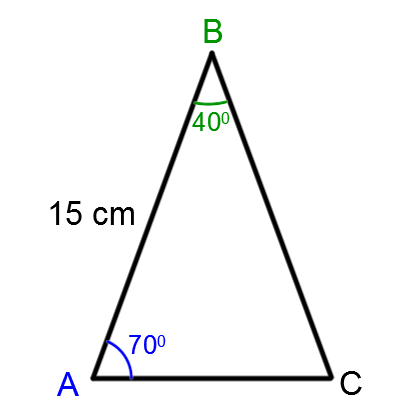
-
Draw the appropriate height
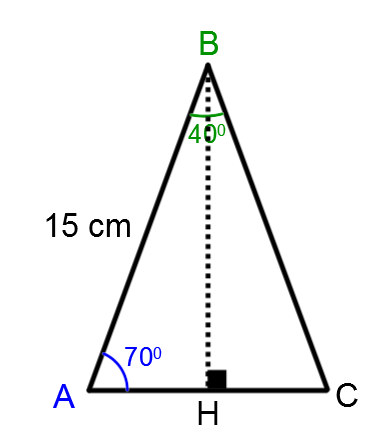
Thus,
||\begin{align}\text{m} \angle C &= 180^\circ - \color{blue}{70^\circ} - \color{green}{40^\circ} \\
&= 70^\circ\\
\Rightarrow \angle C &= \color{blue}{\text{m} \angle A} \\
&= 70^\circ\end{align}||
Therefore, |\Delta ABC | is an isosceles.
-
Use trigonometric ratios
For the height, use the trigonometric ratio associated with the side |\overline {AH}| of |\Delta AHB| :
||\begin{align} \cos \color{blue}{70^\circ} &= \frac{\text{m} \overline{AH}}{15}\\
\Rightarrow m \overline{AH} &= \cos \color{blue}{70^\circ} \times 15\\
&\approx 5.12 \ \text{cm}\\\\
\sin \color{blue}{70^\circ} &= \frac{\color{orange}{m \overline{BH}}}{15} \\
\Rightarrow \color{orange}{m \overline {BH}} &= \sin \color{blue}{70^\circ} \times 15\\
&\approx \color{orange}{14.1 \ \text{cm}}\end{align}||
In addition,
||\begin{align} m \angle BCA &= 180^\circ - \color{blue}{70^\circ} - \color{green}{40^\circ} \\
&= 70^\circ\end{align}||
Since we are dealing with an isosceles triangle,
||\begin{align} \color{red}{\text{m} \overline {AC}} &= 2 \times \text{m} \overline {AH} \\
&= 2 \times 5.12 \\
&= \color{red}{10.24\ \text{cm}}\end{align}|| -
Apply the formula
||\begin{align} A_\text{triangle}&= \frac{\color{red}{\text{base}} \times \color{orange}{\text{height}}}{2}\\
&= \frac{\color{red}{10.24} \times \color{orange}{14.1}}{2}\\
&\approx 72.19 \ \text{cm}^2\end{align}|| -
Interpret the answer
The area of the triangle is approximately 72.19 cm2.
In more complex situations, we only find the measurement of one side, but two measurements of different angles. To achieve the answer, it is necessary to reuse some of the approaches from the previous examples by drawing the height.
To establish a military base at a new location, the Generals from different squadrons sketch the following plan:
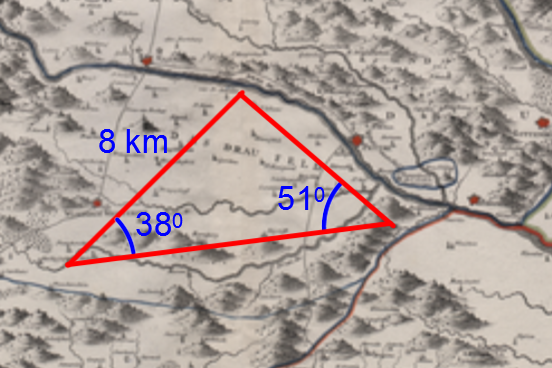
To fit all the soldiers and their equipment, the area of the new base must be at least |25 \ \text{km}^2|. Does the plan above meet this requirement?
-
Draw the appropriate height
To form two right-angled triangles, draw the following height:
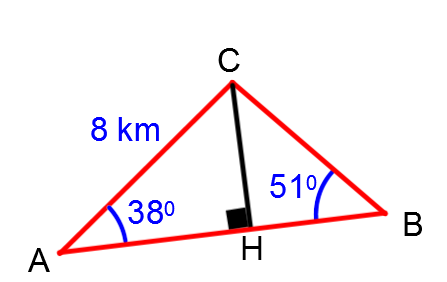
-
Use trigonometric ratios
To calculate the area of the triangle, find |\color{blue}{\text{m} \overline {AB}}| .
||\begin{align}\sin 38^\circ &= \frac{\color{green}{\text{m} \overline {CH}}}{8 \ \text{km}} \\
\color{green}{\text{m} \overline {CH}} &\approx 4.5 \ \text{km}\\\\
\cos 38^\circ &= \frac{\text{m} \overline {AH}}{8 \ \text{km}} \\
\text{m} \overline {AH} &\approx 6.62 \ \text{km}\\\\
\tan 51^\circ &= \frac{\color{green}{\text{m} \overline {CH}}} {\text{m} \overline {BH}} \\
\tan 51^\circ &= \frac{4.5 \ \text{km}}{\text{m} \overline {BH}} \\
\text{m} \overline {BH} &\approx 4.36 \ \text{km}\\\\
\color{blue}{\text{m} \overline{AB}} &= \text{m} \overline {AH} + \text{m} \overline {HB}
\\
&= 6.62 + 4.36 \\
&= \color{blue}{10.98 \ \text{km}}\end{align}|| -
Calculate the area
||\begin{align} A_\text{triangle} &= \frac{\color{blue}{\text{base}} \times \color{green}{\text{height}}}{2}\\
&= \frac { \color{blue}{m \overline{AB}} \times \color{green}{m \overline{CH}}}{2}\\
&= \frac { \color{blue}{10.98} \times \color{green}{4.5}}{2}\\
&\approx 24.71 \ \text{km}^2\end{align}|| -
Interpret the answer
The Generals will have to go back to the drawing board, because the area of the triangle they drew up is less than |25 \ \text{km}^2|.
In the previous example, the sine law could have been used to find |\color{blue}{\text{m} \overline {AB}}.|
To confirm your understanding of trigonometry, consult the following interactive CrashLesson:
