En utilisant les diverses caractéristiques des vecteurs, il est possible de les comparer entre eux afin d'élaborer de nouvelles notions.
En analysant le mot équipollent, on y retrouve le préfixe « équi » dont les racines latines font référence à la notion d'égalité. Dans le contexte des vecteurs, cette égalité touche plusieurs notions.
Deux vecteurs sont équipollents (ou égaux) lorsqu'ils ont la même norme, la même direction et le même sens.
En d'autres mots, il faut que les vecteurs analysés soient identiques en tout point afin d'être qualifiés d'équipollents.
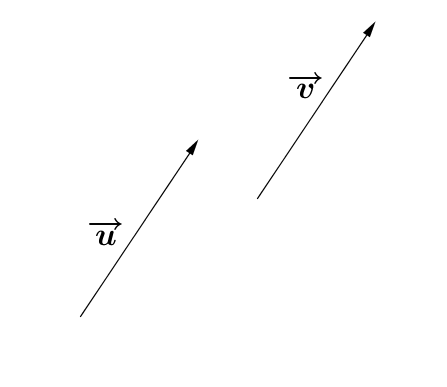
Dans l'exemple précédent, |\overrightarrow u| et |\overrightarrow v| ont une orientation et une norme équivalentes.
En d'autres mots, les composantes |(x_u, y_u)| de |\overrightarrow u| sont les mêmes que les composantes |(x_v, y_v)| de |\overrightarrow v|.
Deux vecteurs sont perpendiculaires (ou orthogonaux) lorsqu’ils se coupent à angle droit.
Ainsi, l'angle qui est formé par l'intersection de deux vecteurs orthogonaux est de |90^\circ .|
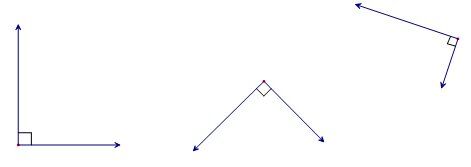
Pour déterminer si deux vecteurs sont perpendiculaires, on peut effectuer le produit scalaire de ceux-ci.
Soit |\overrightarrow{u}=(a,b)| et |\overrightarrow{v}=(c,d).| Deux vecteurs sont orthogonaux si et seulement si : ||\begin{align}\overrightarrow{u} \cdot \overrightarrow{v} &= 0\\ \Rightarrow\ ac + bd &= 0 \end{align}||
En résumé, le produit scalaire de deux vecteurs orthogonaux donne toujours un résultat nul.
En sachant que |\overrightarrow{u}=(\color{red}{4},\color{blue}{1})| et |\overrightarrow{v}=(\color{red}{-2},\color{blue}{8})|, est-ce qu'on peut qualifier ces vecteurs d'orthogonaux?
1. Identifier les composantes des vecteurs
Dans le cas présent, elles sont déjà données.
2. Effectuer le produit scalaire ||\begin{align} \overrightarrow{u}\cdot\overrightarrow{v} &=(\color{red}{4},\color{blue}{1}) \cdot (\color{red}{-2},\color{blue}{8}) \\ &= \color{red}{4 \times -2}+\color{blue}{1 \times 8} \\ &= \color{red}{-8}+\color{blue}{8} \\ &=0 \end{align}||
3. Interpréter la réponse
Puisque le produit scalaire de ces deux vecteurs est égal à 0, ces deux vecteurs sont orthogonaux.
Bien entendu, ce ne sont pas tous les vecteurs qui sont orthogonaux.
En sachant que |\overrightarrow{m}=(\color{blue}{4},\color{red}{3})|et |\overrightarrow{n}=(\color{blue}{-2},\color{red}{6})|, détermine si ces vecteurs sont orthogonaux.
1. Identifier les composantes des vecteurs
Dans ce cas, elles sont fournies.
2. Effectuer le produit scalaire ||\begin{align} \overrightarrow{m} \cdot\overrightarrow{n} &= (\color{blue}{4},\color{red}{3}) \cdot (\color{blue}{-2}, \color{red}{6}) \\ &=\color{blue}{4 \times -2} + \color{red}{3 \times 6} \\ &= \color{blue}{-8} + \color{red}{18} \\ &= 10 \end{align}||
3. Interpréter la réponse
Puisque le produit scalaire de ces deux vecteurs est différent de 0, alors ces vecteurs ne sont pas orthogonaux.
Tout comme la notion d'équipollence des vecteurs, la colinéarité est une autre caractéristique qui met en relation la direction des vecteurs.
Des vecteurs colinéaires, aussi appelés linéairement dépendants, sont des vecteurs qui ont la même direction.
Dans un langage plus commun, des vecteurs colinéaires sont formés de droites qui sont parallèles.
On dit que deux vecteurs sont colinéaires si, en multipliant les composantes de l'un des vecteurs par un scalaire |k| (constante), on obtient les composantes de l'autre vecteur.
Donc, si le vecteur |\overrightarrow{u}| est colinéaire au vecteur |\overrightarrow{v}|, alors il existe un scalaire |k| tel que |\overrightarrow{u}=k\overrightarrow{v}|.
Si on veut utiliser cette caractéristique pour savoir si deux vecteurs sont colinéaires, il faut être en mesure de trouver la valeur de ce scalaire |k.|
Afin d'obtenir le scalaire |k|, on divise la première composante de |\overrightarrow{b}| par la première composante de |\overrightarrow{a}|.
Ensuite, on fait de même avec la deuxième composante de chacun des vecteurs.
Au final, si on obtient le même quotient, les vecteurs seront colinéaires et le quotient correspondra à la valeur du scalaire |k|.
Fait à noter, seule la notion de direction est à considérer pour la colinéarité des vecteurs. Ainsi, la norme et le sens ne jouent aucun rôle dans cette relation.
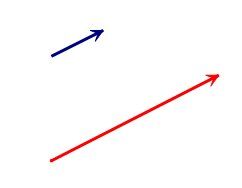
Même direction
Même sens
Normes différentes
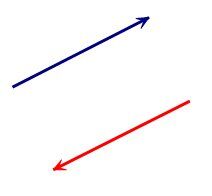
Même direction
Sens différents
Même norme
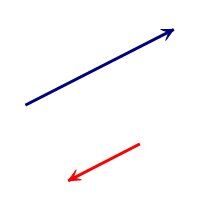
Même direction
Sens différents
Normes différentes
Une fois de plus, il est possible de mettre ces notions en lien avec une démarche arithmétique.
Selon les informations que l'on peut déduire du plan cartésien ci-dessous, détermine si |\color{blue}{\overrightarrow a}| et |\color{red}{\overrightarrow b}| sont linéairement dépendants.
1. Identifier les composantes des vecteurs
Selon le plan cartésien ci-dessus et sa graduation, on sait que : ||\begin{align}\color{blue}{\overrightarrow a}\ &\color{blue}{= (2, 4)}\\ \color{red}{\overrightarrow b}\ &\color{red}{= (-6, -12)} \end{align}||
2. Trouver la valeur du paramètre |k|
Pour la composante en |x| des deux vecteurs, on a : ||\frac{\color{blue}{-6}}{\color{red}{2}} = -3||
Pour la composante en |y| des deux vecteurs, on a : ||\frac{\color{blue}{-12}}{\color{red}{4}} = -3||
3. Interpréter la réponse
Dans le cas présent, la valeur du paramètre |k =-3| pour les deux divisions. Ainsi, ces deux vecteurs sont colinéaires.
Advenant le cas où la division des composantes aurait donné deux résultats différents, |\color{blue}{\overrightarrow a}| et |\color{red}{\overrightarrow b}| n'auraient pas été colinéaires.
Dans l'éventualité où c'est le sens qui différencie deux vecteurs en apparence équipollents, on dira d'eux qu'ils sont des vecteurs opposés.
Deux vecteurs sont opposés s'ils ont la même direction et la même norme, mais qu'ils sont de sens contraire.
Graphiquement parlant, c'est seulement la flèche qui définit le vecteur qui sera différente.
À la lumière du plan cartésien ci-dessous, détermine si |\color{blue}{\overrightarrow a}| et |\color{red}{\overrightarrow b}| sont opposés?
1. Identifier les composantes des vecteurs
||\begin{align}\color{blue}{\overrightarrow a}\ &\color{blue}{= (4,3)} \\ \color{red}{\overrightarrow b}\ &\color{red}{= (-4, -3)} \end{align}||
2. Déterminer si les vecteurs sont colinéaires
||\frac{\color{red}{-4}}{\color{blue}{4}} = -1 \\ \frac{\color{red}{-3}}{\color{blue}{3}} = -1||
Puisque le résultat des divisions est le même, |\color{blue}{\overrightarrow a}| et |\color{red}{\overrightarrow b}| sont colinéaires.
3. Déterminer si les vecteurs ont la même norme
||\begin{align}{\parallel} \color{blue}{\overrightarrow a}{\parallel}^2 &= 3^2 + 4^2 \\ {\parallel} \color{blue}{\overrightarrow a}{\parallel} ^2 &= 25\\ \sqrt{{\parallel} \color{blue}{\overrightarrow a} {\parallel}^2} &= \sqrt{25} \\ {\parallel} \color{blue}{\overrightarrow a} {\parallel} &= 5 \\ \\ {\parallel} \color{red}{\overrightarrow b} {\parallel}^2 &= (-3)^2 + (-4)^2 \\ {\parallel} \color{red}{\overrightarrow b} {\parallel}^2 &= 25 \\ \sqrt{{\parallel} \color{red}{\overrightarrow b}{\parallel}^2} &= \sqrt{25}\\ {\parallel} \color{red}{\overrightarrow b} {\parallel} &= 5 \end{align}||Ainsi, |{\parallel} \color{blue}{\overrightarrow a} {\parallel} = {\parallel} \color{red}{\overrightarrow b} {\parallel} = 5.|
4. Analyser le sens de chaque vecteur
Selon le dessin dans le plan cartésien, on voit bien que les flèches ne pointent pas dans le même sens. Ainsi, |\color{blue}{\overrightarrow a}| et |\color{red}{\overrightarrow b}| sont opposés.
Même si la notion de vecteurs opposés semble plus intuitive que les autres, c'est elle qui demande une démarche plus exhaustive puisqu'elle fait référence à plusieurs notions, soient celles de norme et de colinéarité des vecteurs.
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
