It is possible to compare vectors and define certain notions of equality by considering the various characteristics of vectors.
The word equipollent contains the prefix ‘equi’ which is Latin, and refers to the notion of equality. In the context of vectors, equality involves several different notions.
Two vectors are equipollent when they have the same magnitude and the same direction. Their arrowheads should point in the same direction.
In other words, two vectors under analysis must be completely identical to be called equipollent.

In the above example, |\overrightarrow u| and |\overrightarrow v| have the same direction and magnitude.
In other words, the vector components |(x_u, y_u)| of |\overrightarrow u| are the same as the components |(x_v, y_v)| of |\overrightarrow v.|
Two vectors are perpendicular (or orthogonal) if they intersect at right angles.
So, the angle formed by the intersection of two orthogonal vectors is |90^\circ.|
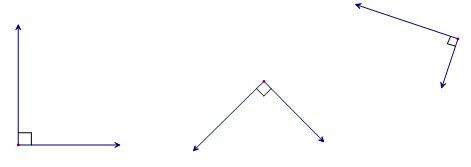
To determine if two vectors are perpendicular, calculate their scalar product (dot product).
So, |\overrightarrow{u}=(a,b)| and |\overrightarrow{v}=(c,d).| Two vectors are orthogonal if and only if : ||\begin{align}\overrightarrow{u} \cdot \overrightarrow{v} &= 0\\ \Rightarrow\ ac + bd &= 0 \end{align}||
In summary, the scalar product or dot product of two orthogonal vectors is always equal to zero.
Consider the vectors |\overrightarrow{u}=(\color{red}{4},\color{blue}{1})| and |\overrightarrow{v}=(\color{red}{-2},\color{blue}{8}).| Are these vectors orthogonal?
-
Identify the components of the vectors
In this case, they are already given. -
Calculate the scalar or dot product ||\begin{align} \overrightarrow{u}\cdot\overrightarrow{v} &=(\color{red}{4},\color{blue}{1}) \cdot (\color{red}{-2},\color{blue}{8}) \\ &= \color{red}{4 \times -2}+\color{blue}{1 \times 8} \\ &= \color{red}{-8}+\color{blue}{8} \\ &=0 \end{align}||
-
Interpret the answer
Since the dot product of the two vectors is equal to |0|, the two vectors are orthogonal.
Remember, not all vectors are orthogonal.
Consider the vectors |\overrightarrow{m}=(\color{blue}{4},\color{red}{3})| and |\overrightarrow{n}=(\color{blue}{-2},\color{red}{6})|. Determine if these vectors are orthogonal.
-
Identify the components of the vectors
In this case, they are already provided. -
Calculate the scalar or dot product ||\begin{align} \overrightarrow{m} \cdot\overrightarrow{n} &= (\color{blue}{4},\color{red}{3}) \cdot (\color{blue}{-2}, \color{red}{6}) \\ &=\color{blue}{4 \times -2} + \color{red}{3 \times 6} \\ &= \color{blue}{-8} + \color{red}{18} \\ &= 10 \end{align}||
-
Interpret the answer
Since the scalar or dot product of these two vectors is not |0|, these vectors are not orthogonal.
Just like the notion of an equipollent vector, collinearity is another characteristic describing the direction of vectors.
Collinear vectors (also called linearly dependent vectors) are parallel vectors whose arrowheads can point in the same or opposite directions.
In other words, collinear vectors are formed by parallel lines.
Two vectors are collinear if one of the vectors is obtained by multiplying the components of the other vector by a scalar |k| (a constant).
So, if the vector |\overrightarrow{u}| is collinear with the vector |\overrightarrow{v}|, then there must exist a scalar |k| such that |\overrightarrow{u}=k\overrightarrow{v}.|
To determine if two vectors are collinear, finding the value of the scalar |k| is essential.
To obtain the scalar |k|, divide the first component of |\overrightarrow{b}| by the first component of |\overrightarrow{a}.|
Then, divide the second components.
If the quotients of both divisions are the same, the vectors are collinear. The quotient corresponds to the value of the scalar |k.|
Note: Only the notion of parallelism is important in the definition of collinearity. Therefore, the magnitudes (norms) and direction (orientation) play no role.
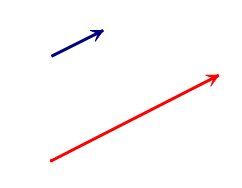
Same direction (orientation)
Different norms (magnitudes)
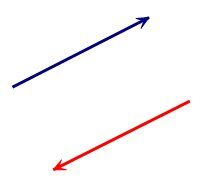
Opposite directions (orientations)
Same norm (magnitude)
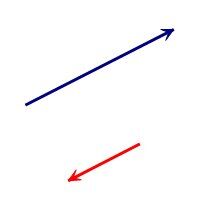
Opposite directions (orientations)
Different norms (magnitudes)
Determining if two vectors are collinear can be simplified into an arithmetic procedure.
Based on the information from the Cartesian plane below, determine whether |\color{blue}{\overrightarrow a}| and |\color{red}{\overrightarrow b}| are linearly dependent.
-
Identify the components of the vectors
According to the Cartesian plane above and its scale, we know that: ||\begin{align}\color{blue}{\overrightarrow a}\ &\color{blue}{= (2, 4)}\\ \color{red}{\overrightarrow b}\ &\color{red}{= (-6, -12)} \end{align}|| -
Find the value of parameter |k|
For the |x| component of the two vectors, the division is: ||\dfrac{\color{blue}{-6}}{\color{red}{2}} = -3||
For the |y| component of the two vectors, the division is: ||\dfrac{\color{blue}{-12}}{\color{red}{4}} = -3|| -
Interpret the answer
In this case, the value of parameter |k =-3| for both divisions. Therefore, these two vectors are linearly dependent (collinear).
If dividing the components had given two different results, |\color{blue}{\overrightarrow a}| and |\color{red}{\overrightarrow b}| would not have been collinear.
If two seemingly equipollent vectors have the opposite direction, they are considered opposite vectors.
Two vectors are opposite if they are collinear and have the same magnitude (norm), but they point in opposite directions.
Graphically speaking, it is only the arrowhead of the vector that will be different.
Based on the Cartesian plane below, determine if |\color{blue}{\overrightarrow a}| and |\color{red}{\overrightarrow b}| are opposite vectors.
-
Identify the components of the vectors ||\begin{align}\color{blue}{\overrightarrow a}\ &\color{blue}{= (4,3)} \\ \color{red}{\overrightarrow b}\ &\color{red}{= (-4, -3)} \end{align}||
-
Determine if the vectors are collinear ||\dfrac{\color{red}{-4}}{\color{blue}{4}} = -1 \\ \dfrac{\color{red}{-3}}{\color{blue}{3}} = -1||
Since the result of the division is the same, |\color{blue}{\overrightarrow a}| and |\color{red}{\overrightarrow b}| are collinear. -
Determine if the vectors have the same magnitude (norm) ||\begin{align}{\parallel} \color{blue}{\overrightarrow a}{\parallel}^2 &= 3^2 + 4^2 \\ {\parallel} \color{blue}{\overrightarrow a}{\parallel} ^2 &= 25\\ \sqrt{{\parallel} \color{blue}{\overrightarrow a} {\parallel}^2} &= \sqrt{25} \\ {\parallel} \color{blue}{\overrightarrow a} {\parallel} &= 5 \\ \\ {\parallel} \color{red}{\overrightarrow b} {\parallel}^2 &= (-3)^2 + (-4)^2 \\ {\parallel} \color{red}{\overrightarrow b} {\parallel}^2 &= 25 \\ \sqrt{{\parallel} \color{red}{\overrightarrow b}{\parallel}^2} &= \sqrt{25}\\ {\parallel} \color{red}{\overrightarrow b} {\parallel} &= 5 \end{align}||Therefore, |{\parallel} \color{blue}{\overrightarrow a} {\parallel} = {\parallel} \color{red}{\overrightarrow b} {\parallel} = 5.|
-
Analyze the orientation of each vector
According to the drawing in the Cartesian plane, the arrows do not point in the same direction. Therefore, |\color{blue}{\overrightarrow a}| and |\color{red}{\overrightarrow b}| are opposite vectors.
Even though the notion of opposite vectors seems more intuitive than the others, verifying that two vectors are opposite requires a more exhaustive approach since the definition refers to several notions, namely, magnitude and collinearity.
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
