On peut effectuer deux sortes de multiplication avec les vecteurs :
Pour effectuer une telle multiplication, on peut faire référence au concept de distributivité de la multiplication.
Soit |k| un scalaire et |\overrightarrow{u}=(a,b)|, alors
||k \overrightarrow{u} = k(a,b)=(ka,kb)||
Comme le scalaire, aussi appelé grandeur scalaire, est un nombre réel, sa multiplication avec un vecteur a un effet sur sa norme.
Lors de la multiplication d'un vecteur par un scalaire, la norme du vecteur résultant sera égale à la norme du vecteur de départ multipliée par |k| en valeur absolue. Ainsi,
-
si | \mid k \mid < 1 \rightarrow| norme du vecteur résultant sera plus petite.
-
si | \mid k \mid = 1 \rightarrow | norme du vecteur résultant sera la même.
-
si | \mid k \mid > 1 \rightarrow | norme du vecteur résultant sera plus grande.
Par contre, il arrive souvent que l'on ne s'intéresse qu'aux composantes du vecteur résultant et non à sa norme.
Quelles sont les composantes de la résultante de |k \overrightarrow {u}| si |\overrightarrow{u}=(3,-2)| et |k = 5|?
1) Effectuer la distributivé du scalaire
||\begin{align} 5 \overrightarrow{u} &= 5 (3, -2) \\
&= (5 \times 3, 5 \times -2) \\
&= (15, -10)\end{align}||
2) Interpréter la réponse
La résultante de |5 \overrightarrow {u} = (15, -10).|
Voici la formule qui permet de calculer le produit scalaire entre deux vecteurs.
Soit |\overrightarrow{u}=(a,b)| et |\overrightarrow{v}=(c,d)|, alors
||\overrightarrow{u}\cdot\overrightarrow{v}=ac+bd||
Remarques : Les vecteurs ne doivent pas être nuls et cette opération est commutative.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Selon cette formule, on voit que le résultat du produit scalaire sera un scalaire (un nombre réel). En analysant les caractéristiques de ce scalaire, on pourra déduire des caractéristiques des deux vecteurs qui ont été multipliés ensemble.</p>
<p>Par exemple, le produit scalaire est utile pour vérifier si deux vecteurs sont <a href="/fr/eleves/bv/mathematiques/la-comparaison-entre-deux-vecteurs-m1301#vecteurs-perpendiculaires-orthogonaux">orthogonaux</a>, pour calculer un <a href="/fr/eleves/bv/physique/le-travail-et-la-puissance-p1024#travail">travail</a> en physique, etc.</p>
</body></html>
Produit vectoriel vs produit scalaire
Comme on vient de le mentionner, le produit scalaire s'écrit à l'aide du symbole |\cdot|. Par exemple, |\overrightarrow{u} \cdot \overrightarrow {v}|.
Par contre, si on utilise une croix (|\times|) pour signifier le produit de deux vecteurs, on qualifiera cette opération de produit vectoriel (notion habituellement étudiée au niveau collégial).
Ainsi,
||\overrightarrow {u} \cdot \overrightarrow{v} \neq \overrightarrow {u} \times \overrightarrow {v}||
Pour en revenir au produit scalaire, on peut appliquer cette théorie de la façon suivante :
Quel est le produit scalaire de |\overrightarrow{u}=(1,2)| et de |\overrightarrow{v}=(3,4)| ?
1) Appliquer la formule
||\begin{align}\overrightarrow{u} \cdot \overrightarrow{v} &= (1,2) \cdot (3,4)\\
&= 1 \times 3 + 2 \times 4\\
&= 3 + 8 \\
&= 11 \end{align}||
2) Interpréter la réponse
Le produit scalaire de |\overrightarrow {u} \cdot \overrightarrow {v} = 11|.
Au niveau de l'interprétation de la réponse, il est difficile d'en tirer des conclusions satisfaisantes s'il n'y a aucun contexte associé aux différents vecteurs. Ainsi, cet exemple avait pour but de montrer le calcul en lien avec le produit scalaire.
Par ailleurs, il existe une autre formule pour effectuer le produit scalaire.
||\overrightarrow{u}\cdot\overrightarrow{v} = {\mid\mid}\overrightarrow{u}{\mid\mid} \times {\mid\mid}\overrightarrow{v}{\mid\mid} \cos \theta||
où |\theta| est la mesure de l'angle en degré formé par les deux vecteurs lorsqu’ils partagent la même origine.
Peu importe la formule utilisée, le résultat et la relation que l'on peut déduire des deux vecteurs impliqués seront les mêmes. Or, le choix de la formule se fait en fonction des informations qui sont fournies dans le problème ou de l'information que l'on doit trouver.
Par ailleurs, les deux formules peuvent être utilisées dans une même démarche.
Soit le vecteur |\overrightarrow{u}=(\color{red}{1},\color{blue}{3})| et le vecteur |\overrightarrow{v}=(\color{green}{2},4)|.
Quelle est la mesure de l'angle |\theta| formé par ces deux vecteurs ?
1) Utiliser la première formule du produit scalaire
||\begin{align} \overrightarrow {u} \cdot \overrightarrow{v} &= \color{red}{a} \times \color{green}{c} + \color{blue}{b} \times d \\
&= \color{red}{1} \times \color{green}{2} + \color{blue}{3} \times 4\\
&= 14 \end{align}||
2) Utiliser la deuxième formule du produit scalaire
En faisant coïncider l'origine de chacun des vecteurs avec l'origine du plan cartésien (0,0), on peut calculer leurs normes de la façon suivante:
||\begin{align}\mid \mid \overrightarrow{u} \mid \mid &=\sqrt{(1 - 0)^2 + (3-0)^2} \\
&= \sqrt{10} \\
& \\
\mid \mid \overrightarrow{v} \mid \mid &=\sqrt{(2-0)^2 + (4-0)^2}\\
&= \sqrt{20} \end{align}||
Ainsi,
||\begin{align}\overrightarrow{u} \cdot \overrightarrow {v} &= {\mid\mid}\overrightarrow{u}{\mid\mid} \times {\mid\mid}\overrightarrow{v}{\mid\mid} \cos \theta \\ &= \sqrt{10}\times \sqrt{20} \cos \theta \\ &= \sqrt{200} \cos \theta \end{align}||
3) Comparer les deux résultats obtenus
Avec l'utilisation des deux formules, on a obtenu deux réponses d'allures différentes, mais qui représentent le même scalaire.
Par comparaison,
||\begin{align} 14 &= \sqrt{200} \cos \theta \\
\frac{14}{\sqrt{200}} &= \cos \theta \\
8{,}13^\circ &\approx \theta \end{align}||
4) Interpréter la réponse
La mesure de l'angle entre les deux vecteurs est d'environ |8{,}13^\circ.|
En appliquant cette démarche à plusieurs reprises dans des contextes et avec des vecteurs qui sont différents, on peut établir certains constats au niveau du scalaire obtenu par le produit scalaire.
-
|\overrightarrow{u} \cdot \overrightarrow{v} > 0 \rightarrow| l'angle |\theta| entre les deux vecteurs est aigu.
-
|\overrightarrow{u} \cdot \overrightarrow{v} < 0 \rightarrow| l'angle |\theta| entre les deux vecteurs est obtus.
-
|\overrightarrow{u} \cdot \overrightarrow{v} = 0 \rightarrow| l'angle |\theta| entre les deux vecteurs est droit.
Regardons comment se démontre le produit scalaire.
Voici le schéma qui servira à la démonstration :
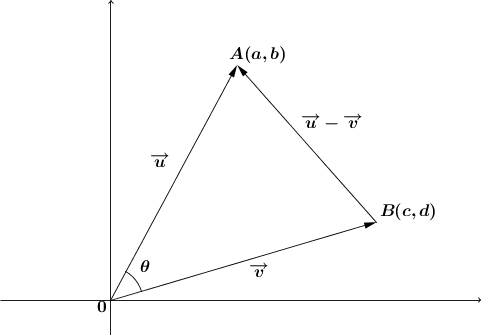
On veut montrer que |\overrightarrow{u} \cdot \overrightarrow{v}=ac+bd.|
On utilise la loi des cosinus qu'on applique au triangle |OAB.|
||\begin{align}\mid \mid \overrightarrow{u} - \overrightarrow{v} \mid \mid^2 &=\mid \mid \overrightarrow{u}\mid \mid^2 + \mid \mid \overrightarrow{v} \mid \mid^2 - 2 \mid \mid \overrightarrow{u}\mid \mid \times \mid \mid \overrightarrow{v}\mid \mid \cos \theta \\ \Rightarrow \mid \mid \overrightarrow{u} \mid \mid \times \mid \mid \overrightarrow{v} \mid \mid \cos \theta&= \dfrac{1}{2} \left(\mid \mid \overrightarrow{u} \mid \mid^2 + \mid \mid \overrightarrow{v} \mid \mid^2 - \mid \mid \overrightarrow{u}-\overrightarrow{v} \mid \mid^2 \right) \end{align}||
Nous savons que :
||\begin{align}\overrightarrow{u} \cdot \overrightarrow{v} &= \mid \mid \overrightarrow{u} \mid \mid \times \mid \mid \overrightarrow{v} \mid \mid \cos \theta \\ &= \frac{1}{2} \left(\mid \mid \overrightarrow{u} \mid \mid^2 + \mid \mid \overrightarrow{v} \mid \mid^2 - \mid \mid \overrightarrow{u} - \overrightarrow{v} \mid \mid^2 \right)\end{align}||
On développe les normes.
||\begin{align} \mid \mid \overrightarrow{u} \mid \mid^2 &= a^2+b^2 \\ \mid \mid \overrightarrow{v} \mid \mid^2 &= c^2+d^2 \\ \mid \mid \overrightarrow{u} - \overrightarrow{v} \mid \mid^2 &= (a-c)^2+(b-d)^2\end{align}||
On remplace :
||\begin{align} \overrightarrow{u} \cdot \overrightarrow{v} &= \frac{1}{2} \left( a^2+b^2 + c^2+d^2 - ((a-c)^2+(b-d)^2) \right) \\
&= \frac{1}{2} \left( a^2 + b^2 + c^2 + d^2 - a^2+2ac-c^2-b^2+2bd-d^2 \right) \\
&= \frac{1}{2} \left( 2ac+2bd \right)\\
&= ac + bd \end{align}||
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
