La composition de fonctions est une opération consistant à remplacer la variable indépendante de la première fonction par l'expression représentant la variable dépendante de la seconde fonction.
Étant donné deux fonctions réelles |f| et |g|, on définit la composition de deux fonctions comme suit :
|(g\circ f)(x)=g(f(x))|
La fonction |(g \circ f)| est appelée la composée de |g| par |f|. On lit cette composée |g| rond |f|.
On peut également avoir |(f \circ g)(x) = f(g(x))| qui est la composée de |f| par |g|. On lit cette cette composée |f| rond |g|.
Il est à noter, qu'en général, les deux composées ne sont pas égales. Donc, la composition n'est pas une opération commutative.
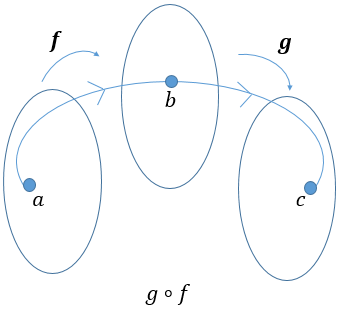
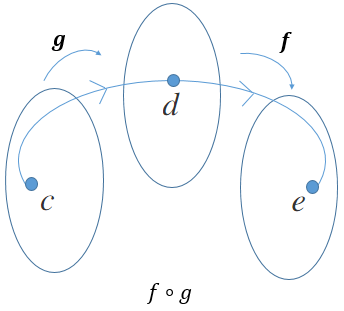
Le domaine de la composition doit tenir compte des restrictions des domaines deux fonctions de départ.
Il ne faut pas confondre le symbole parfois utilisé pour la multiplication avec la symbole de la composition de fonctions.
-
multiplication : |\cdot|
-
composition : |\circ|
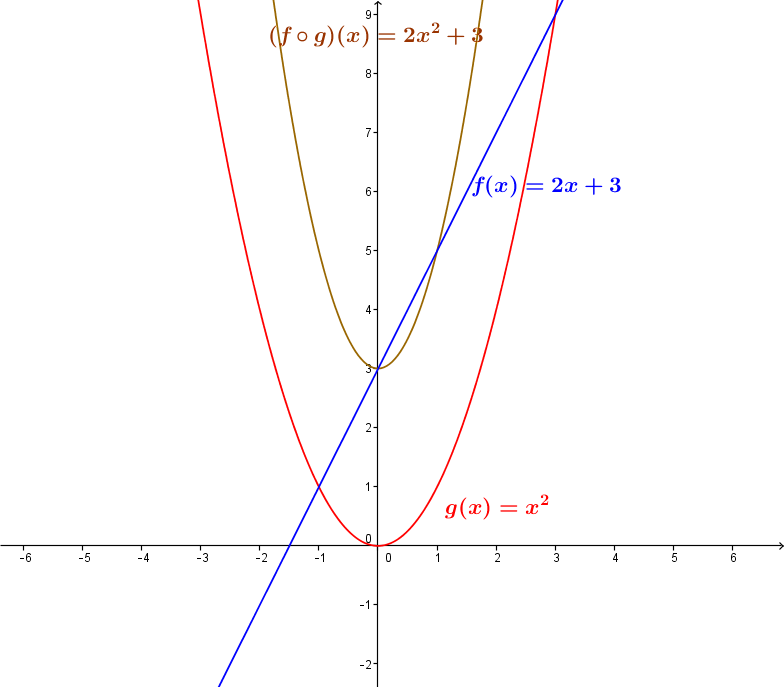
Soit la fonction |f| définie par |f(x)=2x+3| et la fonction |g| définie par |g(x)=x^2.|
La composée |(f \circ g)(x)| se calcule ainsi : ||\begin{align} (f \circ g)(x) &= f\big(g(x)\big) \\ &=f(x^2) \\ &=2( x^2) + 3 \\ &=2x^2+3 \end{align}||
Il n'y a aucune restriction à mettre ici, donc le domaine de cette composition est |\mathbb{R}.|
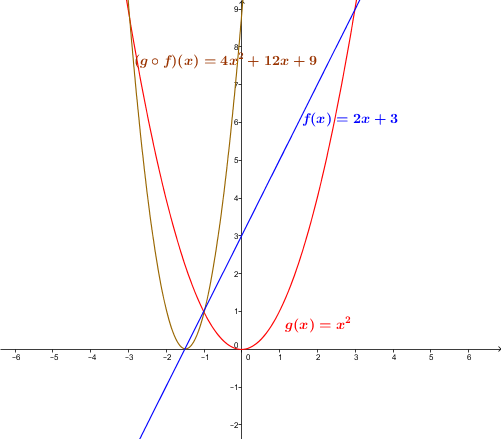
La composée |(g \circ f)(x)| se calcule ainsi : ||\begin{align} (g \circ f)(x) &= g\big(f(x)\big) \\ &=g(2x+3) \\ &=(2x+3)^2 \\ &=(2x+3)(2x+3) \\ &=4x^2+12x+9 \end{align}||
Il n'y a aucune restrictions à mettre ici, donc le domaine de cette composition est |\mathbb{R}.|
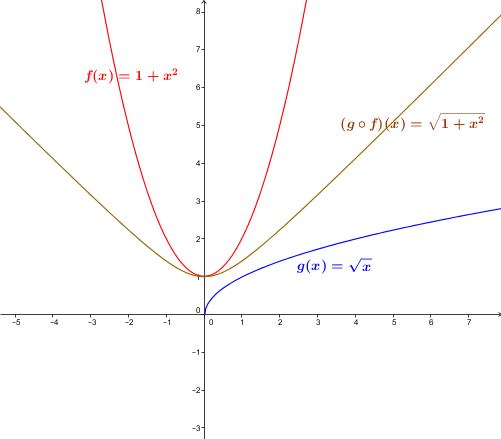
Soit la fonction |f| définie par |f(x)=1+x^2| et la fonction |g| définie par |g(x)=\sqrt{x}.|
La composée |(f \circ g)(x)| se calcule ainsi : ||\begin{align} (f \circ g)(x) &= f\big(g(x)\big) \\ &= f\left(\sqrt{x}\right) \\ &= 1+\left(\sqrt{x}\right)^2 \\ &=1+x \end{align}||
Ici, le domaine est l'ensemble des nombres réels positifs. En fait, sous la racine carrée, on ne peut mettre que des nombres positifs.
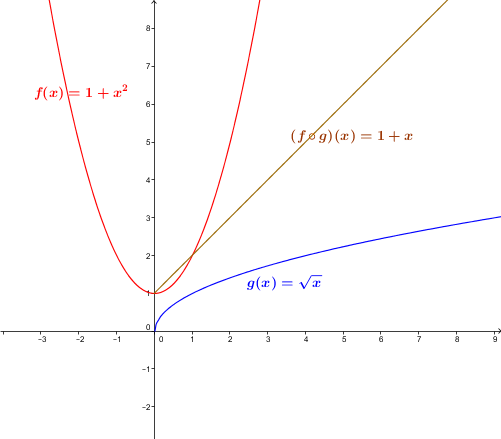
La composée |(g \circ f)(x)| se calcule ainsi : ||\begin{align} (g \circ f)(x) &= g\big(f(x)\big) \\ &=g\left(1+x^2\right) \\ &=\sqrt{1+x^2} \end{align}||
Le domaine de la fonction est l'ensemble des nombres réels. En effet, la fonction |1+x^2| est toujours positive et donc la fonction racine carrée est toujours bien définie.
Pour valider ta compréhension des opérations sur les fonctions de façon interactive, consulte la MiniRécup suivante :
