Une image peut être modifiée selon ce qu'on désire obtenir de celle-ci. Ainsi, nous pouvons effectuer une homothétie (agrandissement ou réduction de l'image), une réflexion, unerotation ou encore, une translation d'une figure afin d'en modifier les dimensions ou l'orientation.
Malgré les différences marquées entre chacune des transformations, il est possible d'en utiliser plus qu'une dans un même contexte.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><a href="/fr/eleves/bv/mathematiques/les-frises-et-les-dallages-m1259">Frise et dallage</a><br>
<a href="/fr/eleves/bv/mathematiques/la-composition-de-transformations-m1261">La composition de transformations</a></p>
</body></html>
En langage mathématique, une image obtenue suite à au moins une de ces modifications aura subi une transformation géométrique.
Une transformation géométrique consiste à déplacer une figure initiale ou à en changer les dimensions pour obtenir une figure image.
Pour différencier la figure initiale de la figure image, on utilise une notation différente au niveau de l'identification des sommets.
Il est important d'identifier les sommets de la figure initiale et finale par des lettres majuscules. Aussi, nous utilisons les même lettres pour les sommets homologues (qui sont situés au même endroit) sur les deux figures. Par contre, ceux de l'image doivent contenir une apostrophe (appelé «prime»).
Finalement, chacune des transformations géométriques ont des propriétés bien précises. Par contre, il existe une propriété qui est associée à la presque majorité des transformations.
Une transformation géométrique est dite isométrique si la figure image conserve les mesures des angles intérieurs homologues sont identiques et les côtés homologues ont les mêmes longueurs que la figure initiale.
Parmi lestransformations isométriques, il y a la translation, la réflexion et la rotation.
L'homothétie N'EST PAS UNE TRANSFORMATION ISOMÉTRIQUE, car les mesures des côtés ne sont pas les mêmes.
Maintenant que les similitudes de chacune des transformations ont été soulevées, il est temps d'aborder les particularités de chacune d'entre elles.
De façon grossière, il s'agit simplement de déplacer une figure simplement en la «glissant» sans modifier son orientation.
Lors d’une translation, on glisse une figure sur une certaine distance. La figure image conserve les mêmes caractéristiques que la figure initiale (mesures de côtés et d'angles). Dans ce cas, on parle d’une transformation isométrique.
Pour en savoir plus sur la translation, consulte les liens suivants :
Cette transformation géométrique est littéralement associée avec les propriétés d'un reflet dans un miroir.
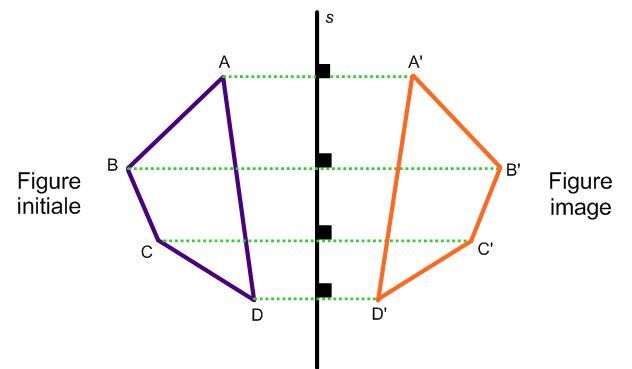
Une réflexion est une transformation géométrique qui donne lieu à une image miroir de la figure initiale. En suivant cette définition, la figure image est inversée par rapport à la figure initiale.
Pour en savoir plus sur la réflexion, consulte les liens suivants :
Comme son nom l'indique, il s'agit de faire tourner la figure d'un certain angle autour d'un point fixe.
Une rotation est une transformation géométrique qui consiste à faire tourner une figure autour d’un point ou d’un axe.
Pour en savoir plus sur la rotation, consulte les liens suivants :
Pour sa part, l'homothétie est la seule transformation géométrique qui modifie les caractéristiques de la figure initiale.
L’homothétie est une transformation géométrique qui consiste à agrandir ou à réduire une figure selon un rapport d’homothétie et un centre d'homothétie.
La figure image obtenue par homothétie conserve les mêmes mesures d'angles intérieurs. Cependant, les côtés homologues n’ont pas la même longueur, mais le rapport de grandeur demeure constant entre tous les côtés homologues.
Pour en savoir plus sur l'homothétie, consulte les liens suivants :