Pour classer les polygones, on fait souvent référence aux mesures des côtés, des angles et des diagonales. Dans certains cas, les mesures des côtés et des angles d'un polygone seront identiques.
On nomme polygone régulier un polygone dont tous les côtés et tous les angles intérieurs ont la même mesure.
On voit que plus un polygone régulier contient de côtés, plus il se rapproche de l'allure d'un cercle.
Il est possible de connaitre le nom des principaux polygones réguliers selon leur nombre de côtés en consultant la fiche sur la classification des polygones.
L'apothème est un segment perpendiculaire aux côtés du polygone qui relie son centre au milieu des côtés qui le composent.
Pour la résolution de problèmes qui font référence à ces notions, il peut être intéressant d'utiliser le théorème de Pythagore.
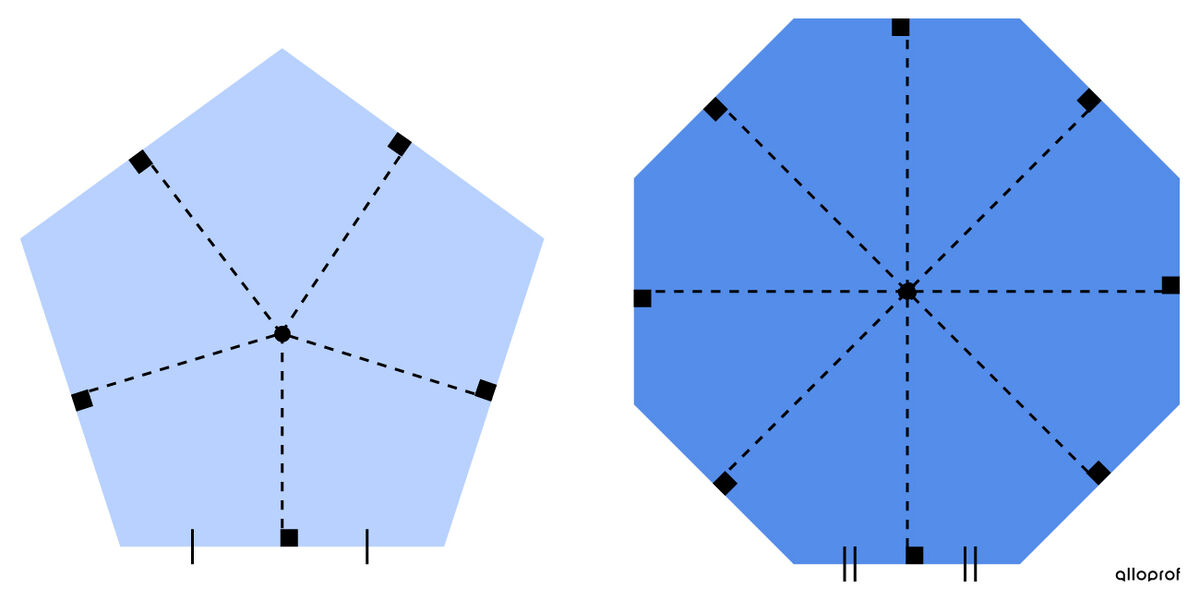
On remarque qu'il y a autant d'apothèmes que de côtés dans un polygone régulier.
Peu importe le polygone régulier avec lequel on travaille, on peut toujours le décomposer en triangles.
Tous les triangles ainsi formés sont des triangles isocèles dont la hauteur correspond à l'apothème du polygone régulier.
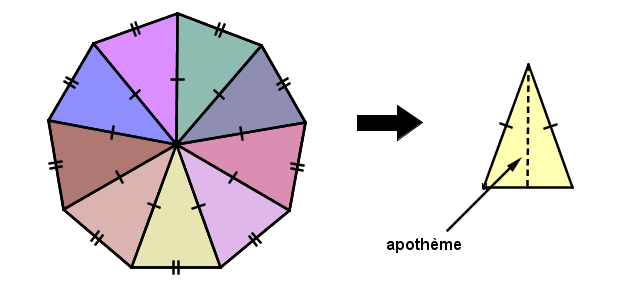
En effet, ces triangles sont isocèles, car les sommets d'un polygone régulier sont situés à égale distance du centre de celui-ci.
Polygone inscrit dans un cercle
Pour bien illustrer l'aspect isocèle des triangles, il est possible de tracer un polygone régulier inscrit dans un cercle. On remarque alors que les côtés des triangles représentés par les segments pointillés sont en fait des rayons du cercle.
Puisque les rayons d'un cercle sont tous égaux, alors les triangles seront tous isocèles. De plus, en considérant que la base de ces triangles correspond aux côtés du polygone régulier, on peut affirmer que tous ces triangles sont isométriques.
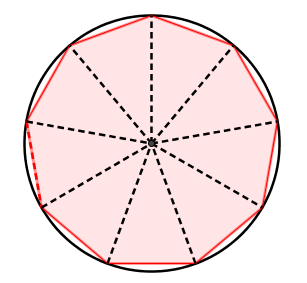
Puisqu'ils sont isocèles et isométriques, on peut déduire la mesure des angles de ces triangles.
L'angle au centre d'un polygone régulier est la valeur de l'angle formé en reliant le centre d'un polygone régulier avec une paire de sommets consécutifs. On peut aussi voir l'angle au centre comme l'angle de l'apex d'un des triangles isocèles qui composent un polygone régulier.
||\text{Valeur d'un angle au centre} =\frac{360^\circ}{n}|| où |n= | nombre de côtés du polygone régulier
En regroupant tous les angles au centre d'un polygone régulier, on obtient un angle plein de |360^\circ .| Puisque les triangles isocèles qui composent un polygone régulier sont isométriques, on déduit que chaque angle au centre a la même mesure.
Quelle est la mesure de l'angle au centre du décagone régulier ci-dessous?
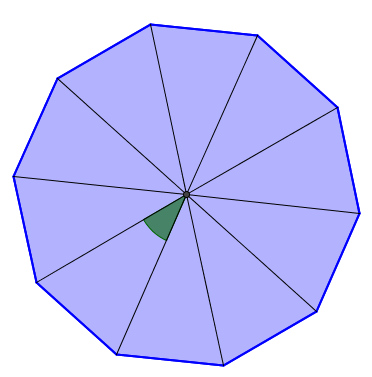
1. Identifier l'angle plein formé par les angles au centre
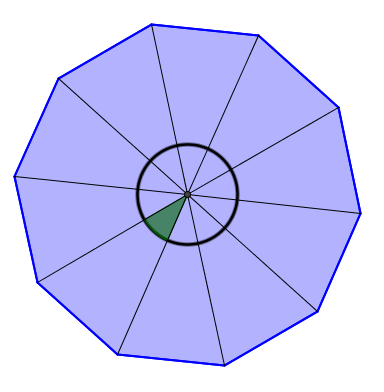
2. Appliquer la formule
||\begin{align*}
\color{green}{\text{valeur de l'angle au centre}} &= \displaystyle \frac{360^\circ}{n} \\
&= \displaystyle \frac{360^\circ}{10} \\
&= \color{green}{36^\circ}
\end{align*}||
Maintenant qu'on connait la valeur de l'un des angles du triangle isocèle entrant dans la composition du polygone régulier, on peut déduire la mesure des deux autres angles. Pour y arriver, on doit se servir des 2 caractéristiques suivantes concernant les triangles isocèles :
-
La somme des angles intérieurs d'un triangle est de |180^\circ .|
-
Un triangle isocèle est également isoangle.
Quelles sont les mesures des angles du triangle ci-dessous considérant que le polygone est régulier?
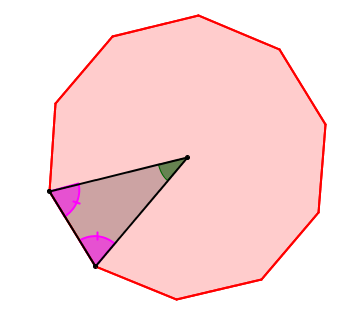
1. Trouver la mesure de l'angle au centre
||\begin{align*}
\color{green}{\text{mesure de l'angle au centre}} &= \displaystyle \frac{360^\circ}{10} \\
&= \color{green}{36^\circ}
\end{align*}||
2. Déduire la mesure des deux autres angles
Puisque c'est un triangle et qu'il est isocèle, ||\begin{align*}
180^\circ &= 2 \times\color{fuchsia}{\text{mesure de l'angle}} + 1 \times \color{green}{\text{mesure de l'angle au centre}}\\
180^\circ &= 2 \times \color{fuchsia}{\text{mesure de l'angle}} + 1 \times \color{green}{36^\circ}\\
144^\circ &= 2 \times\color{fuchsia}{\text{mesure de l'angle}}\\
\color{fuchsia}{72^\circ} &= \color{fuchsia}{\text{mesure de l'angle}}
\end{align*}||
On aurait également pu trouver la mesure d'un angle intérieur du polygone régulier pour ensuite la diviser par deux, toujours en se servant du fait que les triangles présents à l'intérieur d'un polygone régulier sont isocèles et isométriques. Cette démarche est tout aussi valable.
Parmi tous les polygones réguliers, seul l'hexagone est décomposable en triangles équilatéraux.
L'hexagone régulier
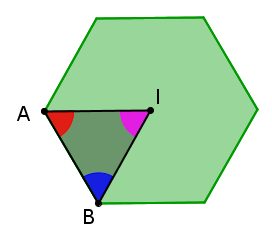
Pour démontrer que |\triangle{ABI}| est bel et bien un triangle équilatéral, on doit déterminer la mesure de chacun des angles.
1. Trouver la mesure de |\color{fuchsia}{\angle AIB}| (angle au centre)
||\begin{align*}
\color{fuchsia}{m\angle{AIB}} &= \displaystyle \frac{360^\circ}{6} \\
&= \color{fuchsia}{60^\circ}
\end{align*}||
2. Trouver la mesure de |\color{red}{\angle IAB}| (moitié d'un angle intérieur)
||\begin{align*}
\color{red}{m\angle IAB} &= \displaystyle \frac{1}{2}\left( \frac{(n-2)\times 180^\circ}{n}\right) \\
&= \displaystyle \frac{1}{2}\left(\frac{(6-2)\times 180^\circ}{6}\right) \\
&= 60^\circ
\end{align*}||
3. Trouver la mesure de |\color{blue}{\angle ABI}|
Puisque la somme des angles intérieurs d'un triangle est de |180^\circ|, on peut utiliser la relation suivante :
||\begin{align*}
180^\circ &= \color{fuchsia}{m\angle AIB} + \color{red}{m\angle IAB} + \color{blue}{m\angle ABI}\\
180 ^\circ &= \color{fuchsia}{60^\circ} + \color{red}{60^\circ} + \color{blue}{m\angle ABI} \\
60^\circ &= \color{blue}{m\angle ABI}
\end{align*}||
4. Tirer une conclusion
Puisque les trois angles ont une mesure de |60^\circ|, alors il s'agit d'un triangle équiangle, donc équilatéral.
Si on veut trouver la mesure d'un seul angle intérieur d'un polygone régulier, il suffit de diviser la somme des mesures des angles intérieurs par le nombre d'angles qu'il contient.
||\begin{align}\text{Mesure d'un angle intérieur}&= \frac{\text{somme des angles intérieurs}}{\text{nombre de côtés du polygone}}\\
&= \frac{(n - 2) \times 180^\circ}{n}\end{align}||
Voici la valeur d'un angle intérieur d'un heptagone régulier.
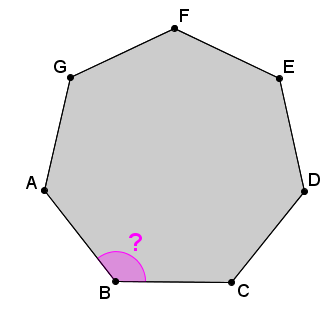
||\begin{align} \text{Mesure d'un angle intérieur} &= \displaystyle \frac{(n-2) \times 180^\circ}{n} \\
&= \frac{(7-2) \times 180^\circ}{7} \\
&\approx 128,57^\circ \end{align}||
Il existe d'autres façons de calculer la mesure d'un angle intérieur d'un polygone régulier. Par exemple, si on a calculé les deux angles isométriques à la base du triangle isocèle qui provient de la décompostion du polygone en triangles, on peut facilement trouver la mesure de l'angle intérieur. L'exemple qui suit montre comment y arriver.
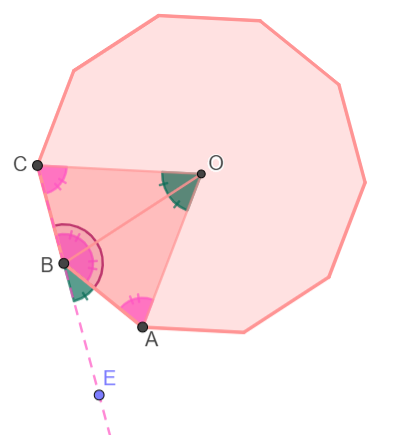
Ici, toutes les mesures du triangle isocèle |OAB| avaient été calculées. On remarque que l'angle |\color{red}{ABC}| est formé des angles |\color{fuchsia}{\angle ABO}| et |\color{fuchsia}{\angle OBC}| qui sont isométriques.
||\begin{align*}\color{red}{\text{Mesure d'un angle intérieur}} &= 2\times\color{fuchsia}{m\angle ABO}\\&= 2\times 72^\circ\\&=144^\circ\end{align*}||
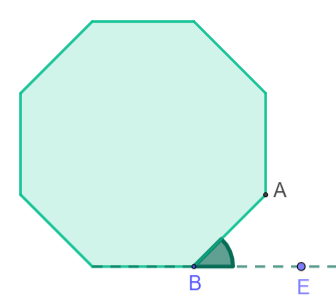
Un angle extérieur d'un polygone est un angle compris entre un côté du polygone et le prolongement du côté adjacent.
Sur la figure ci-dessous, l'angle |ABE| est un angle extérieur.
Un polygone a autant d'angles extérieurs qu'il a de côtés.
La somme des angles extérieurs de tout polygone convexe vaut toujours 360°. L'animation ci-dessous, qui montre les 9 angles extérieurs d'un ennéagone, permet de le visualiser (tu peux démarrer l'animation en appuyant sur le bouton « jouer » dans le bas à gauche).
Si on veut trouver la mesure d'un seul angle extérieur d'un polygone régulier, il suffit de diviser la somme des angles du polygone, qui est toujours de 360°, par le nombre d'angles qu'il contient, qui est le même que le nombre de côtés.
||\begin{align}\text{Mesure d'un angle extérieur}&= \frac{360°}{\text{nombre de côtés du polygone}}\\ &= \frac{360°}{n}\end{align}||
Voici la valeur d'un angle extérieur d'un pentagone régulier.
||\begin{align} \text{Mesure d'un angle extérieur} &= \displaystyle \frac{360^\circ}{n} \\
&= \frac{360^\circ}{5} \\
&=72^\circ \end{align}||
On peut aussi calculer la mesure d'un angle extérieur à partir de la mesure de l'angle intérieur.
L'angle intérieur et l'angle extérieur d'un polygone sont supplémentaires. De cette information, on peut obtenir les deux formules suivantes :
|\text{mesure d'un angle extérieur}=180°-\text{mesure d'un angle intérieur}|
et
|\text{mesure d'un angle intérieur}=180°-\text{mesure d'un angle extérieur}|
Soit le polygone régulier suivant :
Dans le tableau suivant, on trouve toutes les façons de calculer les mesures d'angles dans les polygones réguliers à partir des autres mesures. Voici comment on doit lire le tableau : la rangée du haut donne la mesure qui est connue, tandis que la première colonne précise la mesure qu'on cherche. Dans toutes les formules, la variable |n| représente le nombre de côtés du polygone régulier.
| Mesure connue |\rightarrow| Mesure à trouver |\downarrow| |
Angle au centre
|(\color{#05BF8E}{m\angle centre})|
|
Angle extérieur
|(\color{#076C56}{m\angle ext})|
|
Angle intérieur
|(\color{#2753B6}{m\angle int})|
|
Angles isoangles du triangle isocèle
|(\color{#FF55C3}{m\angle ABO})|
|
Somme des angles intérieurs
|(\sum \angle int)|
|
| |\color{#05BF8E}{m\angle centre}=| | | |\color{#076C56}{m\angle ext}| | |180°-\color{#2753B6}{m\angle int}| | |180°-2 (\color{#FF55C3}{m\angle ABO})| | |180°-\dfrac{\sum \angle int}{n}| |
| |\color{#076C56}{m\angle ext}=| | |\color{#05BF8E}{m\angle centre}| | | |180°-\color{#2753B6}{m\angle int}| | |180°-2 (\color{#FF55C3}{m\angle ABO})| | |180°-\dfrac{\sum \angle int}{n}| |
|
|\color{#2753B6}{m\angle int}=|
|
|180°-\color{#05BF8E}{m\angle centre}| | |180°-\color{#076C56}{m\angle ext}| | | |2 (\color{#FF55C3}{m\angle ABO})| | |\dfrac{\sum \angle int}{n}| |
| |\color{#FF55C3}{m\angle ABO}=| | |\dfrac{180°-\color{#05BF8E}{m\angle centre}}{2}| | |\dfrac{180°-\color{#076C56}{m\angle ext}}{2}| | |\dfrac{\color{#2753B6}{m\angle int}}{2}| | | |\dfrac{\sum \angle int}{n}\div 2| |
| |\sum \angle int=| | |n (180°-\color{#05BF8E}{m\angle centre})| | |n (180°-\color{#076C56}{m\angle ext})| | |n (\color{#2753B6}{m\angle int})| | |n \big(2(\color{#FF55C3}{m\angle ABO})\big)| | |
Dans l'animation interactive suivante, on peut observer les angles au centre, de même que les angles intérieurs et extérieurs des polygones réguliers de 3 à 15 côtés.
Puisque les mesures des angles et des côtés sont isométriques, il est possible de tracer plusieurs axes de symétrie dans un polygone régulier.
Un polygone régulier possède autant d'axes de symétrie que de côtés. Ainsi, un triangle équilatéral possède trois axes de symétrie tandis qu'un hexagone régulier en possède six.
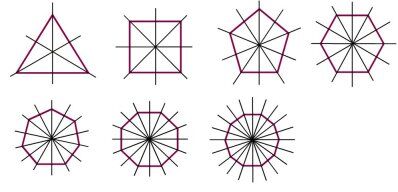
Comme point de repère pour dessiner les axes de symétrie , on peut se fier aux sommets du polygone et au point milieu de chacun des côtés.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><a href="/fr/eleves/bv/jeux/la-foire"><img alt="image" src="/sites/default/files/inline-images/LaFoire_0.jpg"></a></p>
</body></html>