La distance entre deux droites parallèles correspond à la longueur du plus court segment de droite qui les sépare et qui leur est perpendiculaire.
La distance entre deux droites parallèles est donc donnée par la longueur du segment qui leur est perpendiculaire et les relie. Pour déterminer cette longueur, il est possible de procéder de trois façons différentes, en fonction de ce qu'on connait.
-
Si on connait les coordonnées d’un point d’une des droites et l’équation de l’autre droite, on peut utiliser la formule de la distance entre un point et une droite pour déterminer la distance recherchée.
-
Si on ne connait pas les coordonnées d’un point d’une des droites, on peut les déterminer à partir de l’équation de la droite, en posant une valeur de |x| et en trouvant la valeur de |y| correspondante. On utilise ensuite la formule de la distance entre un point et une droite pour déterminer la distance recherchée.
-
Si on ne connait pas les coordonnées d’un point d’une des droites, il est aussi possible d'appliquer la formule suivante.
||\text{dist}=\dfrac{\mid b_1-b_2\mid}{\sqrt{a^2+1}}||Cette formule utilise les paramètres des équations des 2 droites :
|y_1 = ax + b_1| et |y_2 = ax + b_2.|
Quelle est la distance entre les droites suivantes?
|d_1 : y = 3x-4| et |d_2 : y = 3x-2|
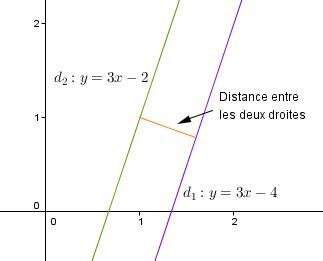
On se sert de la formule de la distance entre deux droites.||\begin{align}\text{dist}&=\dfrac{\mid b_1-b_2\mid}{\sqrt{a^2+1}}\\[3pt]&=\dfrac{\mid(-4)-(-2)\mid}{\sqrt{3^2+1}}\\[3pt]&=\dfrac{\mid-2\mid}{\sqrt{10}}\\[3pt]&\approx0{,}63\end{align}||La distance est d'environ |0{,}63| unité.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Si les coordonnées d'un point avaient été connues, ou si on préférait les déterminer, il aurait été nécessaire d'utiliser la formule de la <a href="/fr/eleves/bv/mathematiques/la-distance-d-un-point-a-une-droite-dans-un-plan-m1315">distance entre un point et une droite</a>.</p>
</body></html>