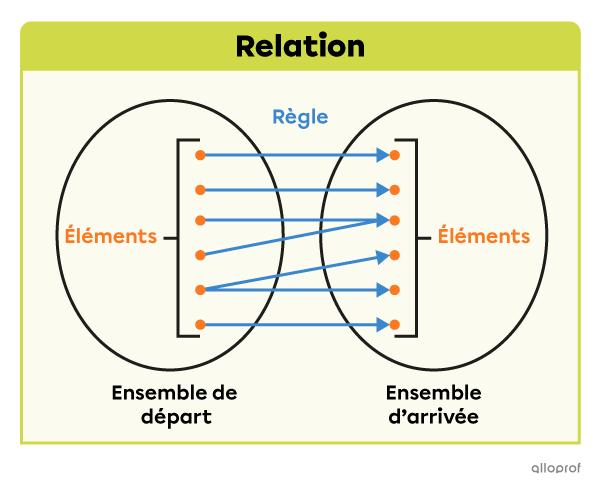
En mathématiques, une relation est un énoncé qui définit un lien entre plusieurs éléments. Chaque relation contient une règle qui établit la correspondance entre des éléments d’un ensemble de départ et des éléments d’un ensemble d’arrivée.
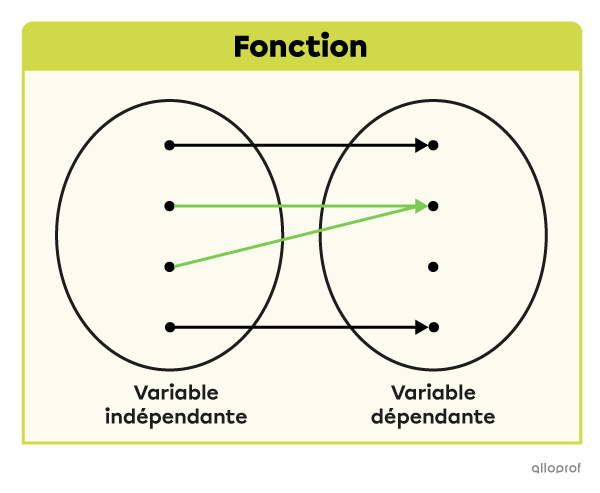
Cette relation est une fonction puisque chaque élément de la variable indépendante est associé à un seul élément de la variable dépendante.
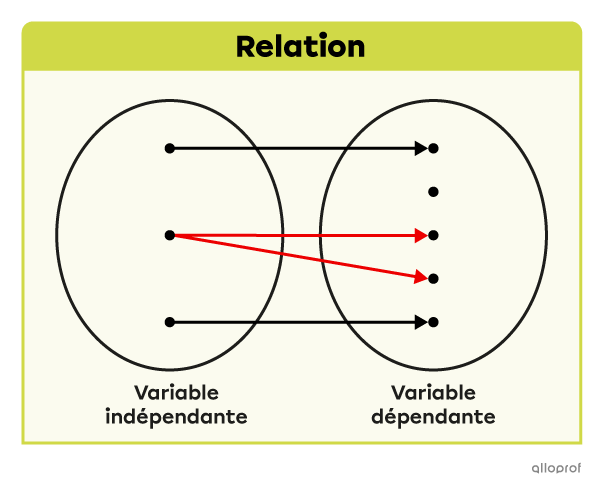
Cette relation n’est pas une fonction puisqu’il y a un élément de la variable indépendante qui est associé à plusieurs éléments de la variable dépendante.
Il est possible de déterminer si une relation est une fonction à l’aide de son graphique. Pour y arriver, il suffit d’utiliser le test de la droite verticale.
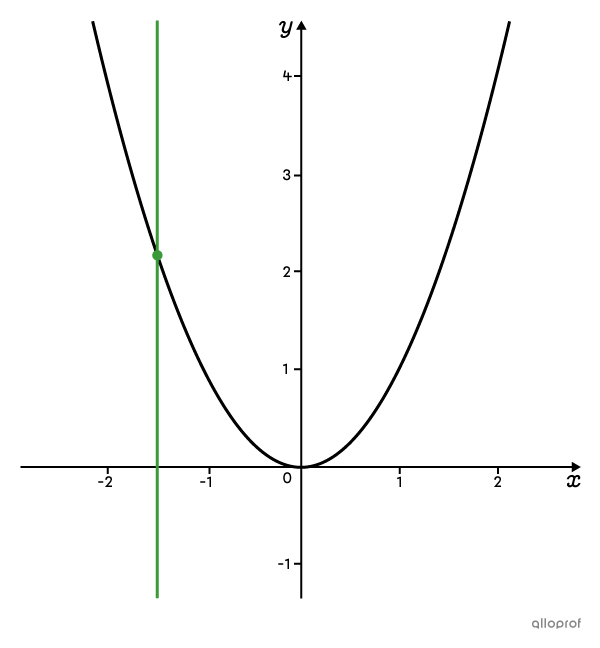
Cette relation est une fonction puisque la droite verticale croise la courbe à un seul endroit peu importe où on la place.
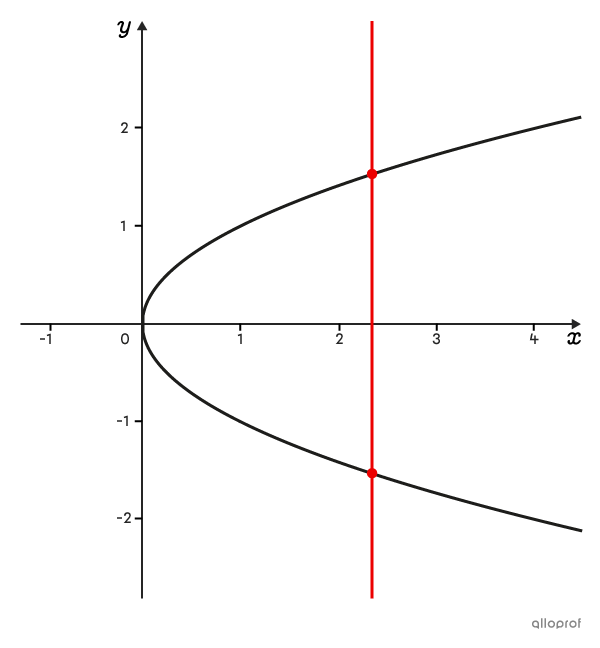
Cette relation n’est pas une fonction puisqu’on peut placer la droite verticale de sorte qu’elle croise la courbe à 2 endroits différents.
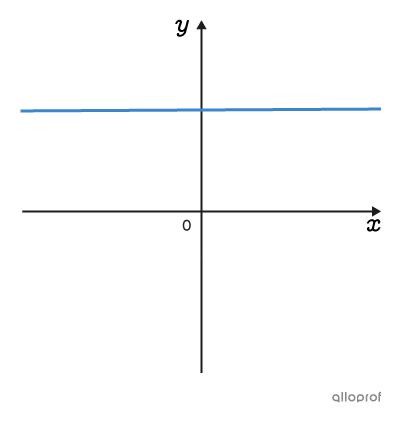
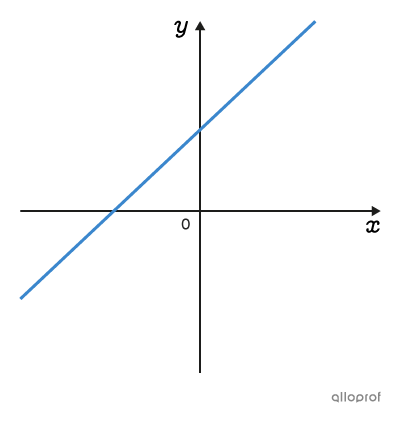
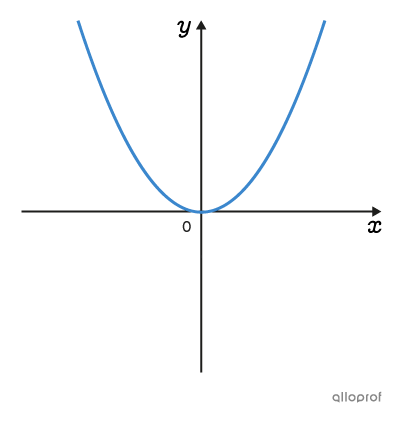
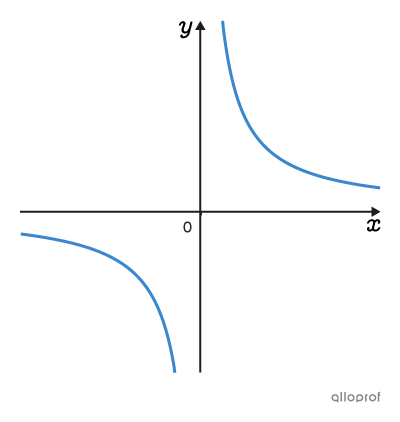
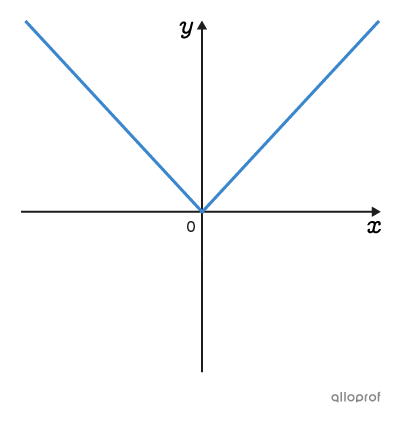
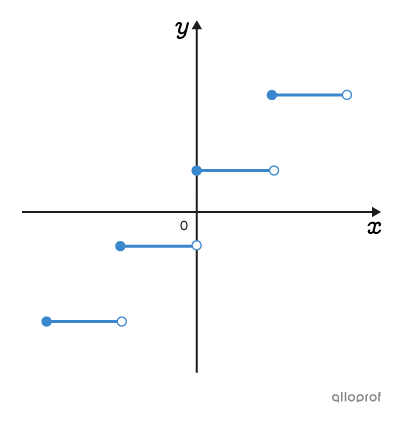
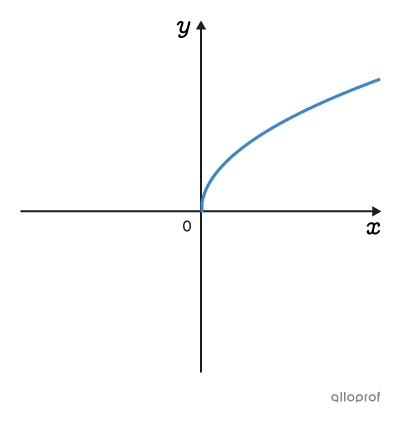
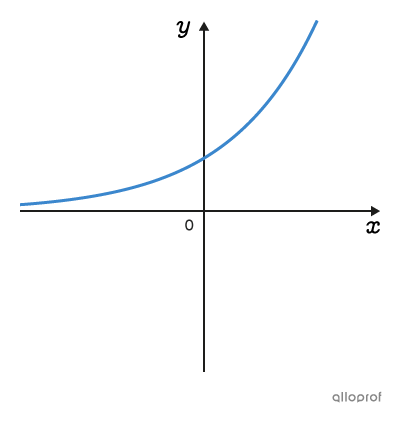
On peut représenter graphiquement une multitude de situations à l’aide de plusieurs familles de fonctions. Les fonctions d’une même famille ont des graphiques et des règles ayant des caractéristiques communes.
Clique sur les images pour en savoir plus.
Fonction polynomiale de degré 0
Fonction polynomiale de degré 1
Fonction polynomiale de degré 2
Fonction rationnelle
Fonction valeur absolue
Fonction en escalier
Fonction racine carrée
Fonction exponentielle
Fonction logarithmique
Fonction définie par partie
Fonction périodique
Fonction trigonométrique
On écrit souvent la règle d’une fonction sous la forme |y=\text{règle}.| Toutefois, on utilise aussi la notation |f(x)=\text{règle,}| qui se lit « |f| de |x| » et qui signifie « la valeur de |f| selon la valeur de |x| ».
Autrement dit, |y| et |f(x)| sont 2 notations équivalentes qui servent à désigner la variable dépendante.
Soit la fonction |y=2x+3,| que l’on peut également écrire |f(x)=2x+3.|
Pour calculer la valeur de la fonction lorsque |x=5,| les calculs peuvent s’écrire des 2 façons suivantes.
||\begin{align}y&=2x+3\\y&=2(5)+3\\y&=13\end{align}||
||\begin{align}f(x)&=2x+3\\f(5)&=2(5)+3\\f(5)&=13\end{align}||
Ainsi, le couple |(5,13)| fait partie de cette fonction.
On peut aussi écrire une fonction en utilisant la notation fonctionnelle. Cette notation sert à définir une fonction en indiquant son ensemble de départ, son ensemble d’arrivée et sa règle de correspondance.
||\begin{align}f:\ \ \begin{gathered}\text{Ensemble}\\\text{de départ}\end{gathered}\ \ \,&\rightarrow\quad\begin{gathered}\text{Ensemble}\\\text{d’arrivée}\end{gathered}\\[3pt]\begin{gathered}\text{Variable}\\\text{indépendante}\end{gathered}&\mapsto\begin{gathered}\text{Règle de}\\\text{correspondance}\end{gathered}\end{align}||
Soit la fonction |f(x)=3x+4.| En utilisant la notation fonctionnelle, on peut écrire cette fonction de la façon suivante.||\begin{align}f:\mathbb{R}&\rightarrow\mathbb{R}\\[3pt]x&\mapsto3x+4\end{align}||L’ensemble de départ est |\mathbb{R},| l’ensemble d’arrivée est aussi |\mathbb{R}| et la règle de correspondance est |3x+4.| De plus, la variable indépendante est |x| et la variable dépendante est |f(x).|
On lit cette notation fonctionnelle de la façon suivante.
« La fonction |f| va de |\mathbb{R}| vers |\mathbb{R}| et associe à un élément |x| de l’ensemble de départ un élément |3x+4| de l’ensemble d’arrivée. »
Pour valider ta compréhension à propos des fonctions de façon interactive, consulte la MiniRécup suivante.
