Voici les deux façons de déterminer la réciproque d'une fonction logarithmique :
Afin de déterminer graphiquement la réciproque d'une fonction logarithmique, on peut procéder de la manière suivante :
Tracer la réciproque de la fonction logarithmique suivante : ||y = -6\log_5 (x+4)+3||
1. On trace la fonction logarithmique dont on souhaite tracer la réciproque.
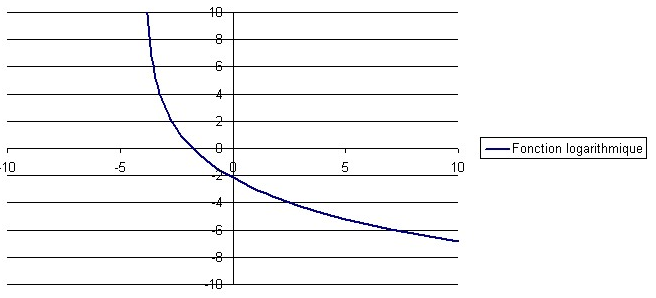
2. On trace la droite |y = x.|
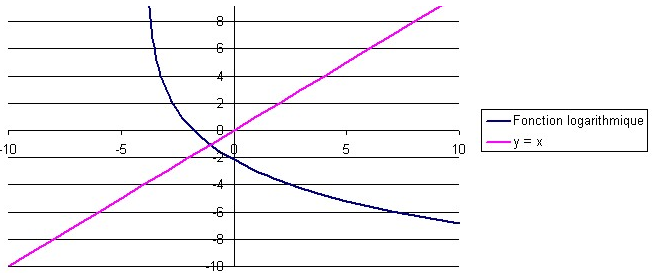
3. On effectue une réflexion de la fonction logarithmique de départ par rapport à la droite |y = x.|
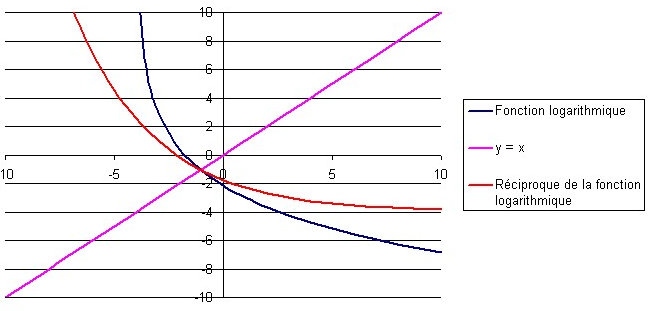
On obtient ainsi la réciproque de la fonction logarithmique de départ.
Afin de déterminer algébriquement la réciproque d'une fonction logarithmique, on peut procéder de la manière suivante :
-
Intervertir les variables |x| et |y| dans la règle initiale.
-
Isoler l'expression contenant le logarithme.
-
Passer à la forme exponentielle pour isoler |y.|
Déterminer algébriquement la règle de la réciproque de la fonction logarithmique suivante:
||y = -4\log_7 (3(x-6))+8||
1. Intervertir les variables |x| et |y| dans la règle initiale.
||x = -4\log_7 (3(y-6))+8||
2. Isoler l'expression contenant le logarithme.
||\begin{align} x &= -4\log_7 (3(y-6))+8 \\ x - 8 &= -4\log_7 (3(y-6)) \\ \frac{\text{-}1}{4}(x - 8) &= log_7 (3(y-6)) \end{align}||
3. Passer à la forme exponentielle pour isoler |y|.
||\begin{align} 7^{\frac{\text{-}1}{4}(x-8)} &= 3(y - 6) \\ \frac{7^{\frac{\text{-}1}{4}(x-8)}}{3} &= y - 6\\ \frac{7^{\frac{\text{-}1}{4}(x-8)}}{3}+6 &= y \\
\small{\frac{1} {3}}\normalsize(7)^{\frac{\text{-}1}{4}(x-8)}+6&= y \end{align}|| Ainsi, | y^{-1} = \dfrac{1}{3}(7)^{\frac{\text{-}1}{4}(x-8)}+6| est la règle de la réciproque.
Il est à noter que les réciproques des fonctions logarithmiques sont des fonctions exponentielles.
Si on observe attentivement la fonction de départ et sa réciproque, voici ce qu'on remarque :
-
Le paramètre |h| devient le paramètre |k| de la réciproque.
-
Le paramètre |k| devient le paramètre |h| de la réciproque.
-
La base |c| de la réciproque est la même que celle de la fonction de départ.
-
Le paramètre |a| de la réciproque est l'inverse du paramètre |b| de la fonction de départ.
-
Le paramètre |b| de la réciproque est l'inverse du paramètre |a| de la fonction de départ.
||y = \color{red}{a}\log_\color{magenta}{c} \big(\color{purple}{b}(x-\color{blue}{h})\big)+\color{green}{k}\ \ \Leftrightarrow \ \ y^{-1}=\color{purple}{\frac{1}{b}}(\color{magenta}{c})^{\color{red}{\frac{1}{a}}(x-\color{green}{k})}+\color{blue}{h}||