La fonction logarithmique est la réciproque de la fonction exponentielle. C’est une fonction qui comporte une asymptote verticale et dont le domaine est restreint.
Lorsqu’on travaille avec la fonction logarithmique, on utilise plusieurs lois et calculs propres aux logarithmes. D’autres notions connexes peuvent aussi être consultées.
Les logarithmes
Notions connexes
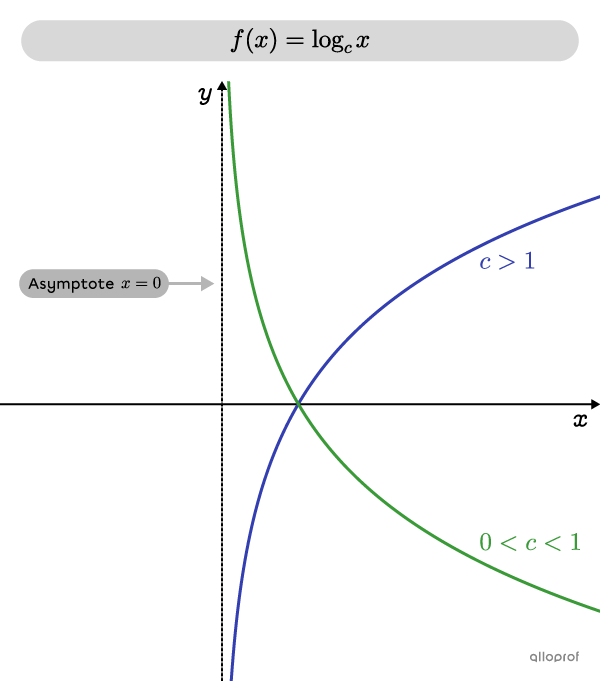
La règle de la fonction logarithmique de base est |f(x)=\log_cx| où |c\neq 1| et |c>0.|
L’argument du logarithme |(x)| doit être supérieur à |0.|
-
La fonction logarithmique de base se rapproche de plus en plus de l’axe des ordonnées, sans jamais y toucher. L’axe des ordonnées correspond donc à une asymptote verticale.
-
La fonction logarithmique de base possède un zéro, mais ne possède pas d’ordonnée à l’origine.
-
Les points de la fonction sont tous situés à droite de l’asymptote. Ainsi, son domaine est l’intervalle |]0,\infty[.|
-
Si |\color{#333FB1}{c>1},| la fonction est croissante.
-
Si |\color{#3A9A38}{0<c<1},| la fonction est décroissante.
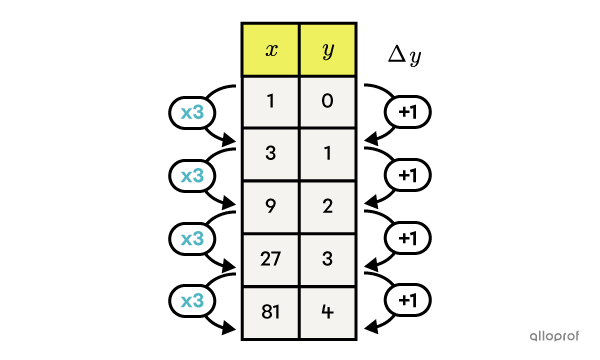
Dans une fonction logarithmique, la variable indépendante correspond à la puissance et la variable dépendante correspond à l’exposant. Ainsi, lorsque la variable dépendante (l’exposant) augmente d’une unité, la variable indépendante (la puissance) varie selon un facteur multiplicatif de |\color{#51B6C2}c.|
Voici un exemple avec la fonction |f(x)=\log_\color{#51B6C2}3x.|||\begin{align}f(x)&=\log_\color{#51B6C2}3x\\\\0&=\log_\color{#51B6C2}3(1)\\1&=\log_\color{#51B6C2}3(3)\\2&=\log_\color{#51B6C2}3(9)\\3&=\log_\color{#51B6C2}3(27)\\ 4&=\log_\color{#51B6C2}3(81) \\&\quad\cdots\end{align}||
Les 2 bases les plus souvent utilisées sont les bases |10| et |e.|
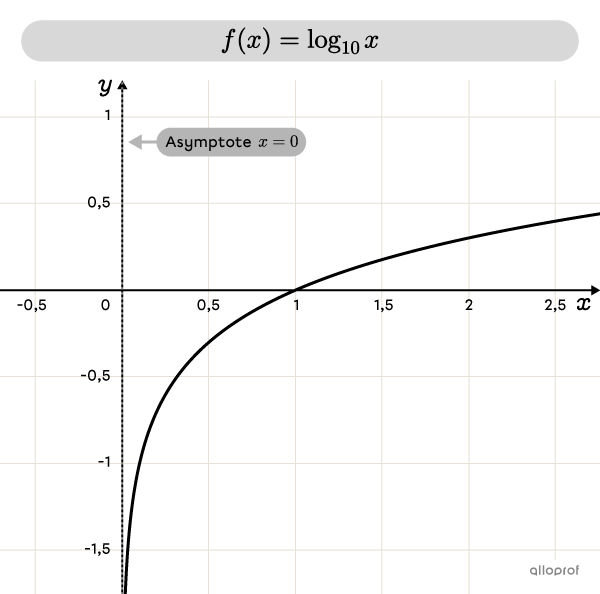
Logarithme en base |\boldsymbol{10}|
Lorsqu’un logarithme est en base |10,| on l’écrit simplement sans sa base. Le logarithme en base |10| est souvent utilisé pour effectuer des calculs à l’aide de la calculatrice, qui elle, est en base |10.|
|\log_{10}x=\log x|
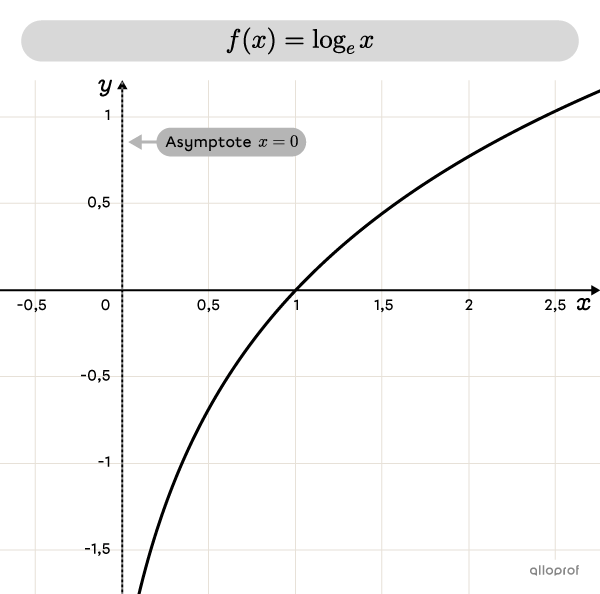
Logarithme en base |\boldsymbol{e}|
Le logarithme en base |e| est appelé logarithme naturel ou logarithme népérien. Le nombre |e,| aussi appelé nombre d’Euler, est un nombre irrationnel, c’est-à-dire qu’il a un développement non périodique et infini.
|\log_e x=\ln x| où |e\approx 2{,}72|
On s’intéresse à 2 types de règles lorsque la fonction logarithmique est transformée.
La forme |\boldsymbol{f(x)=a\log_c(bx)}|
où
|a\neq 0,| |b\neq 0,| |c\neq 1,| |c>0|
et
|x=0| correspond à l’équation de l’asymptote verticale.
L’argument du logarithme |(bx)| doit être supérieur à |0.|
La forme |\boldsymbol{f(x)=a\log_c\big(b(x-h)\big)+k}|
où
|a\neq 0,| |b\neq 0,| |c\neq 1,| |c>0|
et
|x=h| correspond à l’équation de l’asymptote verticale.
L’argument du logarithme |\big(b(x-h)\big)| doit être supérieur à |0.|
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction logarithmique de façon interactive, consulte la MiniRécup suivante.
