Il arrive que l’expression fonction quadratique soit utilisée comme synonyme de fonction polynomiale de degré 2. Par souci de cohérence, l’utilisation de l’expression fonction polynomiale de degré 2 est privilégiée.
Pour aborder la fonction polynomiale de degré 2, il importe de définir certains termes. De plus, d’autres notions connexes peuvent être consultées.
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction polynomiale de degré 2 de façon interactive, consulte la MiniRécup suivante.

La fonction de base |f(x)=x^2| est représentée par la table de valeurs et le graphique suivants.
| |x| | |y| |
|---|---|
| |-3| | |9| |
| |-2| | |4| |
| |-1| | |1| |
| |0| | |0| |
| |1| | |1| |
| |2| | |4| |
| |3| | |9| |
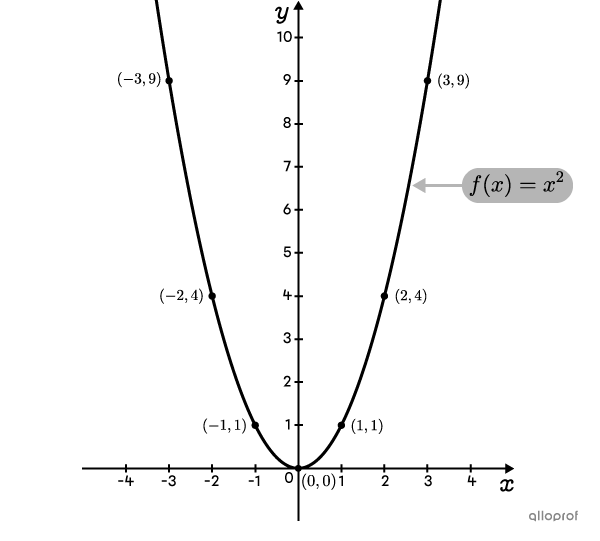
On remarque avec la forme parabolique de la fonction qu’il y a un sommet et que celui-ci est situé à l’origine |(0,0)| du plan cartésien. Également, les 2 branches de la parabole sont symétriques par rapport à un axe vertical qui passe par le sommet. Dans le cas de la fonction de base, il s’agit de l’axe des ordonnées.
La règle de la fonction polynomiale de degré 2 peut s’écrire sous 4 formes.
La forme centrée à l’origine : |f(x)=ax^2|
La forme générale : |f(x)=ax^2+bx+c|
La forme canonique : |f(x)=a(x-h)^2+k|
La forme factorisée : |f(x)=a(x-x_1)(x-x_2)|
Pour une fonction polynomiale de degré 2, lorsque la variable indépendante augmente d’une unité, l’écart entre les variations de la variable dépendante est constant et vaut |2a.| On utilise la fonction |f(x)=2(x-1)^2+1| en exemple.
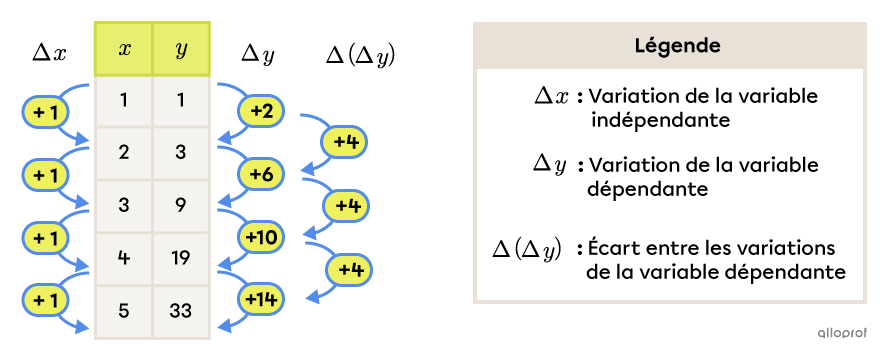
Chaque écart entre les variations consécutives de la variable dépendante vaut |4| ou |2a.| Or, si |2a=4,| alors |a=2.| C’est bel et bien la valeur du paramètre |a.|