Il est possible de représenter une inéquation dans un plan cartésien. Voici les différents cas possibles.
Une droite frontière est une droite qui délimite l'ensemble-solution d'une inéquation.
Il est possible de représenter une inéquation dans un plan cartésien. Pour ce faire, certaines règles doivent être suivies :
Pour tracer une inéquation :
-
Tracer la fonction dans le plan cartésien, comme si on avait une égalité (droite frontière).
-
Indiquer le type d'inégalité.
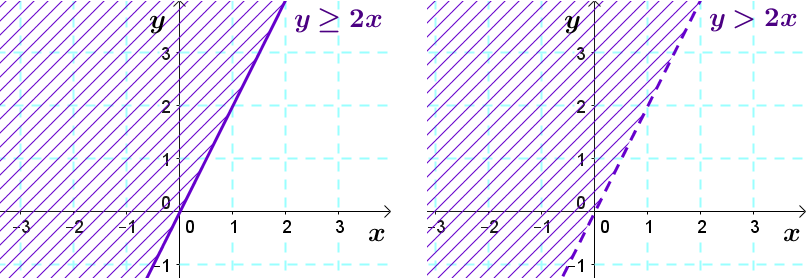
Si le signe de l'inéquation est |<| ou |>,| on tracera la droite frontière pointillée. Les points sur la droite ne font pas partie de la solution.
Si le signe de l'inéquation est |\leq| ou |\geq,| on tracera la droite frontière pleine. Les points sur la droite font partie de la solution.
-
Déterminer la région-solution.
Puisqu’il existe une infinité de points dans le plan cartésien qui peuvent répondre à cette contrainte et qu’il est impossible de tous les définir précisément, on hachurera la portion du plan cartésien qui illustre toutes ces possibilités. -
Valider la région-solution.
On valide la région-solution en remplaçant les variables de l'inéquation par les coordonnées d'un point se trouvant dans la région-solution. On appelle ce point un point test ou encore un point d'essai.
La droite frontière de gauche est incluse dans l'ensemble-solution alors que celle de droite en est exclue.
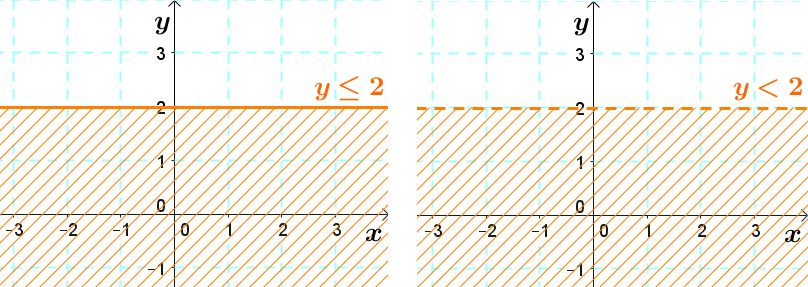
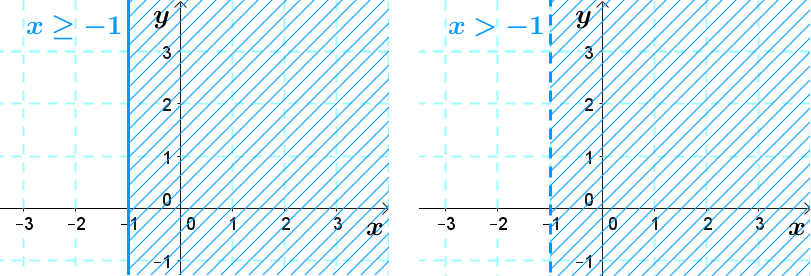
On doit se souvenir qu’une droite peut être horizontale (|y =| constante) ou verticale (|x=|constante).
Lorsque |y| est égal à une constante, la représentation de la frontière est sous forme d'une droite horizontale.
Lorsque |x| est égal à une constante, la représentation de la frontière est sous forme d'une droite verticale.
Il est possible, en suivant les étapes énumérées auparavant, de représenter une inéquation linéaire à deux variables dans un plan cartésien.
Soit la fonction |y > 3x+6.|
-
On représente tout d’abord la droite frontière dans le plan cartésien, comme si on avait une égalité |(y = 3x + 6).|
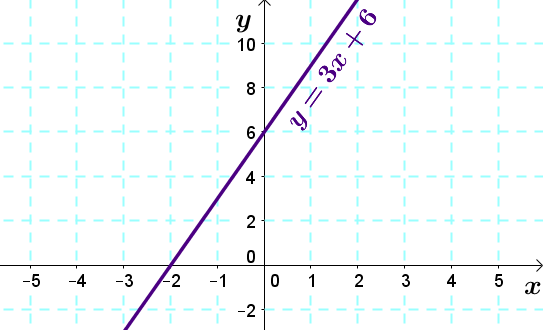
-
Comme le signe est |>,| on trace la droite frontière en trait pointillé.
(Truc : On peut simplement effacer des bouts de la ligne à l'étape précédente.)
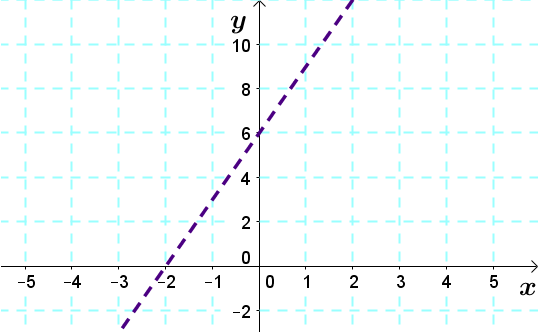
-
On détermine la région-solution.
Pour ce faire, on peut prendre un point dans la plan cartésien et vérifier s'il valide l'inéquation. Prenons le point |\left(0,0\right).|
On remplace |x| et |y| dans l'équation par les coordonnées du point et on résout l'inéquation.||\begin{align}0&> 3(0)+6\\0 &> 0+6\\0 &\color{red}{>} 6\end{align}|||0| n'est pas plus grand que |6| donc le point |\left(0,0\right)| ne fait pas partie de la solution. On hachure donc de l'autre côté de la droite frontière (en haut à gauche).
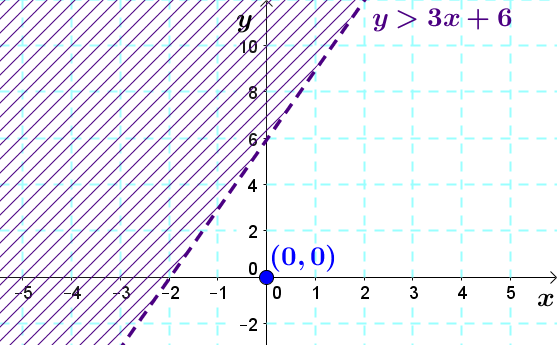
Après avoir tracé la droite frontière et déterminé le type d'inégalité, il est possible de déterminer la région-solution en utilisant un point aléatoire du plan cartésien. Il suffit alors de remplacer les variables de l'inéquation par les coordonnées de ce point et de vérifier si elles valident ou non l'inéquation. Ainsi:
- Si le point test valide l'inéquation, il fait partie de la région à hachurer, c'est-à-dire de la région-solution.
- Si le point test ne valide pas l'inéquation, il ne fait pas partie de la région à hachurer, c'est-à-dire de la région-solution. Il faut alors hachurer la région opposée.
-
On trouve l'équation de la droite frontière sous la forme |y=ax+b.|
-
On détermine le signe d'inégalité approprié (en utilisant la méthode du point d'essai).
Si le trait est pointillé on a 2 choix : |>| ou |<.|
Si le trait est plein on a 2 choix : |\geq| ou |\leq.|
Soit le graphique suivant.
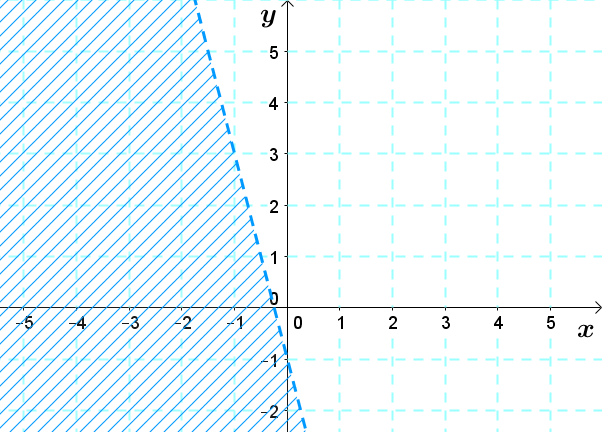
La droite frontière passe par les points |\left(-1,3\right)| et |\left(0,-1\right).|
-
Pour trouver l'équation de la droite frontière, on doit calculer le |a.| ||\begin{align}a &= \dfrac{\Delta y}{\Delta x}\\[3pt] &= \frac{y_2-y_1}{x_2-x_1}\\[3pt] &=\frac{-1-3}{0- -1}\\[3pt] &=-4\end{align}||On a donc |y=-4x+b.|
Il faut maintenant calculer |b| en remplaçant |x| et |y| par les valeurs d'un point. ||\begin{align}3&= -4 (-1) + b\\3 &= 4 + b\\-1&=b\end{align}||L'équation de la droite frontière est |y=-4x-1.|
-
Il ne reste qu'à déterminer le signe d'inégalité.
Comme le trait est pointillé, on a 2 choix : |>| ou |<.|
On choisit |<| et on vérifie si c'est le bon signe en prenant un point d'essai appartenant à la zone hachurée. Prenons le point |(-1,0).| ||\begin{align}0 &< -4 (-1) - 1\\0 &< 4 - 1\\0&<3\end{align}||Ceci est vrai, donc le signe d'inégalité est adéquat.
Par conséquent, le graphique plus haut correspond bien à l'inéquation |y<-4x-1.|
Lorsque l'on représente deux inéquations dans un plan cartésien, on se retrouve avec une zone où les zones hachurées de chaque inéquation se rencontrent. Cette zone de rencontre représente la région-solution.
Soit les 2 inéquations suivantes.||\begin{align}y&>2x-2 & y&<-2x+3\end{align}||
-
On trace les 2 inéquations comme si elles étaient des équations.
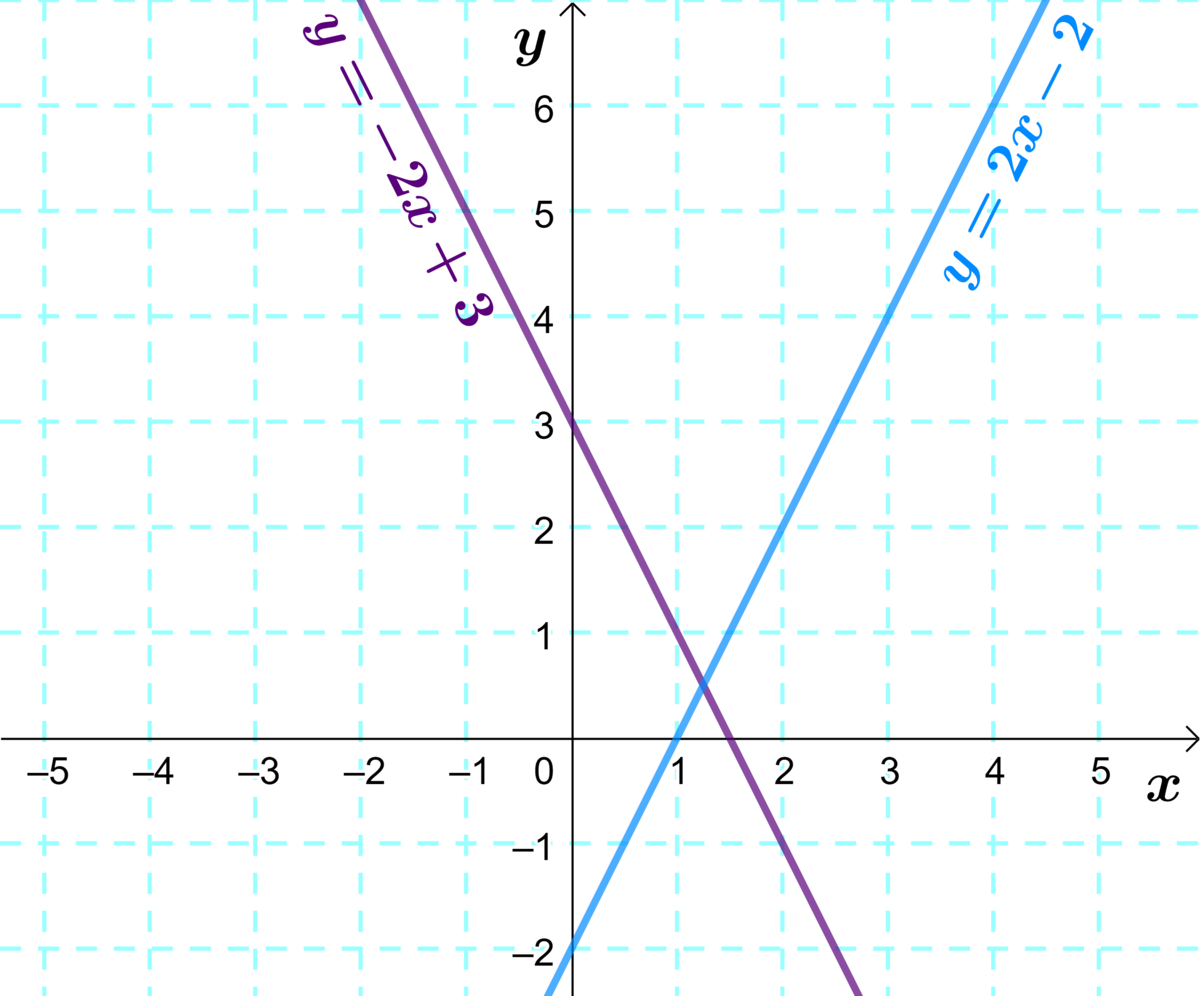
-
Puisque les signes sont |>| et |<,| les droites frontières seront pointillées.
-
On détermine les zones à hachurer. Prenons le point |(0,0)| pour les 2 inéquations.
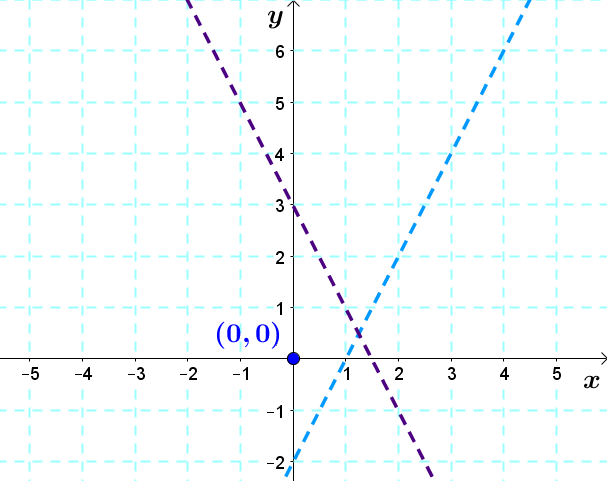
||\begin{align}0&>2 (0)-2 & &\phantom{00000} & 0&<-2 (0) +3\\0&>-2 & &\phantom{0} & 0&<3\\&\text{Vrai} & &\phantom{0} & & \text{Vrai}\end{align}||Dans les 2 cas, la situation est vraie et donc on hachure vers le point |(0,0)| pour les 2 inéquations.
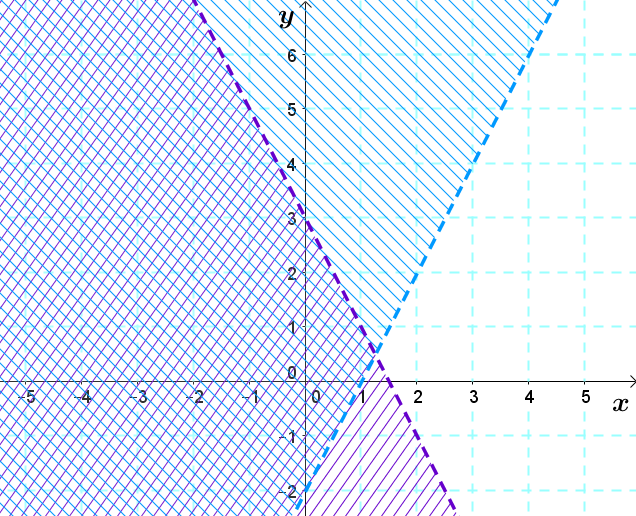
La région où les zones hachurées se rencontrent correspond à la région-solution. C'est ce qu'on appelle l'intersection des 2 inéquations.
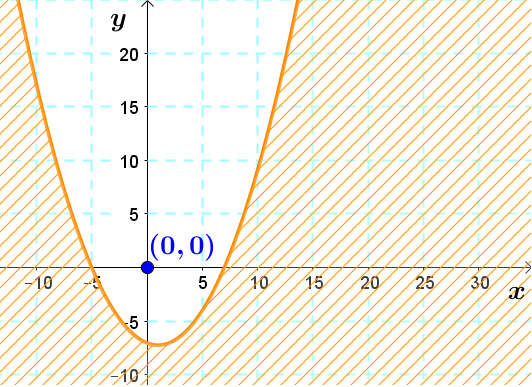
Il est possible, en suivant les étapes énumérées auparavant, de représenter une inéquation de degré 2 à deux variables dans un plan cartésien.
Soit l'inéquation |y \le 0{,}2x^2 - 0{,}4x - 7|
Dans ce cas, l'inéquation contient une égalité. Il faut donc représenter la fonction à l'aide d'une ligne pleine.
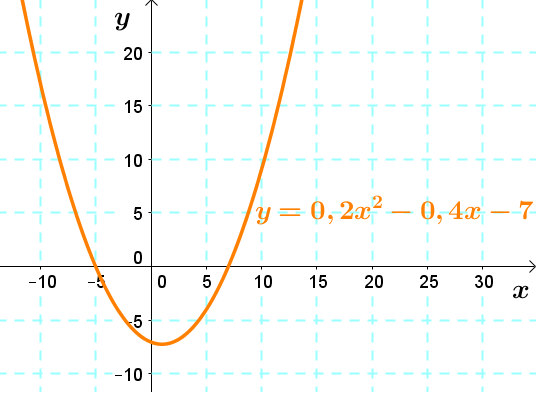
Ensuite, il suffit d'utiliser un point test pour valider quelle zone doit être sélectionnée comme région-solution. Par exemple, on peut utiliser le point |(0,0).| ||\begin{align}0 &\le 0{,}2(0)^2 - 0{,}4(0) - 7\\ 0 &\le -7\end{align}||Cette réponse est fausse puisque |0| est plus grand que |-7,| il faut donc sélectionner la zone où le point |(0,0)| ne se retrouve pas.