Pour résoudre un problème impliquant une fonction partie entière, il est important de bien connaitre tous les rouages de cette fonction. Il est également important de savoir résoudre algébriquement une telle équation dans un problème hors contexte. Pour les explications sur la façon de procéder, consulte la fiche suivante : Résoudre une équation partie entière.
Jean-Marc a besoin des services d’un avocat pour régler un litige avec son propriétaire par rapport à certaines clauses de son bail. Il contacte maitre Labonté, un avocat spécialisé dans ce type de cause. Les honoraires de l’avocat se détaillent comme suit : pour chaque période partielle ou complète de |15| minutes, Me Labonté facture |45| $. Heureusement, les taxes sont incluses.
a) Si l’étude du dossier demande |3\ h\ 24| de travail à Me Labonté, combien cela coutera-t-il à Jean-Marc?
b) Au moment où la cause est complètement réglée, Jean-Marc calcule qu’il a payé un montant total de |2\ 700| $ en frais d’avocat. Combien d’heures Me Labonté lui a-t-il facturées en tout?
On commence par définir les variables :
|x| : Temps facturé (h)
|f(x)| : Frais totaux ($)
Remarque : Pour les unités de la variable |x|, on a choisi d’utiliser les heures, car c'est l'unité qui est exigée à la question b). Si on avait choisi d'utiliser les minutes comme unité de temps, la règle aurait été différente, mais on aurait obtenu les mêmes réponses finales.
On peut représenter la situation dans un plan cartésien.
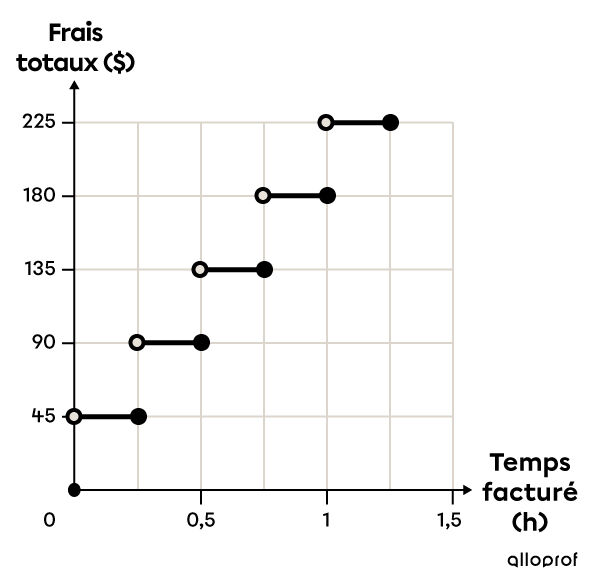
On place un point à l’origine du plan cartésien, car si Jean-Marc n’engage pas l’avocat |(\text{temps} = 0\ h),| ce dernier ne lui facturera rien |(\text{frais} = 0\ $)!| Puis, dès que Jean-Marc commence à le faire travailler sur son dossier, même pour une seule minute, les honoraires de Me Labonté sont facturés à Jean-Marc, c’est pourquoi il y a une marche à |45\ $| pour un temps entre |0| et |0{,}25\ h| |(15| minutes |=| un quart d’heure |=| |0{,}25\ h).|
On détermine la valeur des paramètres |a| et |b| en analysant les données du problème :
-
Puisque la distance verticale entre chaque marche correspond à une augmentation des frais de |45\ $,| on a que |{\mid}a{\mid} = 45.|
-
Comme la longueur de chaque segment correspond à la durée entre les augmentations de cout, soit |0{,}25\ h,| on a que |{\mid}b{\mid}=\dfrac{1}{0{,}25}=4.|
-
Chaque segment a un point ouvert à gauche et un point fermé à droite. On en déduit que |b| est négatif. Donc |{\mid}b{\mid} = -4.|
-
Étant donné que l’escalier est croissant, on en déduit que les paramètres |a| et |b| sont du même signe et& donc que |a| est négatif aussi. Alors, |a = -45.|
On peut utiliser la règle |f(x) = a[bx],| car il y a un point fermé à |(0,0).| En remplaçant les paramètres |a| et |b| par les valeurs qu’on vient de déterminer, on obtient la règle de la fonction : ||f(x) = -45[-4x]||
On peut maintenant répondre aux deux questions.
a)
On cherche la valeur de |f(x)| lorsque |x = 3\ h\ 24.|
Attention! |3\ h\ 24 \neq 3{,}24\ h.| Il faut convertir ce temps en nombre décimal en procédant comme suit : ||3\ h\ 24 = 3\ h + \frac{24}{60} h = 3{,}4\ h||
Maintenant, on peut remplacer |x| par |3{,}4| dans la règle de la fonction. ||\begin{align}f(x) &= -45[-4x] \\ f(3{,}4) &= -45[-4(3{,}4)] \\ &= -45[-13{,}6] \\ &= -45(-14) \\ &=\ \ 630\ $\end{align}||
Réponse : Jean-Marc devra payer |630\ $| en honoraires.
b)
On cherche la ou les valeur(s) de |x| lorsque |f(x) = 2\ 700\ $|
On remplace donc |f(x)| par |2\ 700| dans la règle et on isole |x.| ||\begin{align}f(x) &= -45[-4x] \\ 2\ 700 &= -45[-4x] \\ \frac{2\ 700}{-45} &= \frac{-45[-4x]}{-45} \\ -60 &= [-4x] \\ \end{align}||
Comme la partie entière est égale à un nombre entier, on peut poursuivre la résolution.
On applique la définition de la partie entière. ||\begin{align}-60 = [-4x]\quad \Longleftrightarrow\quad -60 \leq\ -4&x\ < -60+1 \\ -60 \leq\ -4&x\ <-59 \\ \frac{-60}{-4}\leq\ \frac{-4}{-4}&x\ <\frac{-59}{-4} \\ 15 \geq\quad\quad &x\ >14{,}75 \end{align}||
Réponse : Me Labonté a facturé entre |14{,}75| et |15| heures en honoraires. On peut aussi donner la réponse en intervalle : |]14{,}75\ ; 15]\ h.|
Dominik loue des films à son club vidéo préféré une fois par semaine. Malheureusement, ce dernier a la fâcheuse habitude de ne pas retourner ses films à temps. Un film coute |2{,}50\ $| lors de la première journée. Il faut absolument retourner le film après une journée sinon il doit payer des frais supplémentaires de |3{,}00\ $| par jour de retard.
a) Déterminez l'équation de la fonction modélisant cette situation et tracez le graphique.
b) Combien Dominik doit-il payer s'il rapporte son film |6| jours plus tard?
a)
La fonction qui modélise cette situation est une fonction en escalier de la forme |y=a[b(x-h)]+k| où |x| est le nombre de jours et |y| la somme à payer.
On peut trouver la valeur de la contremarche |(a)| qui correspond à la somme à payer chaque jour. Dans ce cas-ci, on paye |3{,}00\ $| par jour. Ainsi, le |a| vaut |3.| On déterminera le signe à lui donner plus tard.
De plus, on peut trouver la valeur de |b| en utilisant la longueur de la marche.
En effet, on a la relation |\text{longueur de la marche} = \dfrac{1}{{\mid}b{\mid}}.|
Dans cet exemple, la longueur de la marche équivaut à |1| jour. Ainsi, |{\mid}b{\mid} = 1.|
Il ne reste qu'à déterminer les coordonnées d'un point plein pour obtenir le couple |(h,k)|. Le premier point plein est |(1;2{,}5).|
Le sens des points est vide-plein. Ainsi, le paramètre |b| doit être négatif. Par conséquent, |b=-1.|
La fonction est croissante alors |ab >0| et ainsi |a=-3.|
En résumé, |a=-3,| |b=-1,| |h=1| et |k=2{,}5.|
Réponses : L'équation est |y=-3[-1(x-1)]+2{,}5| et on obtient le graphique suivant :
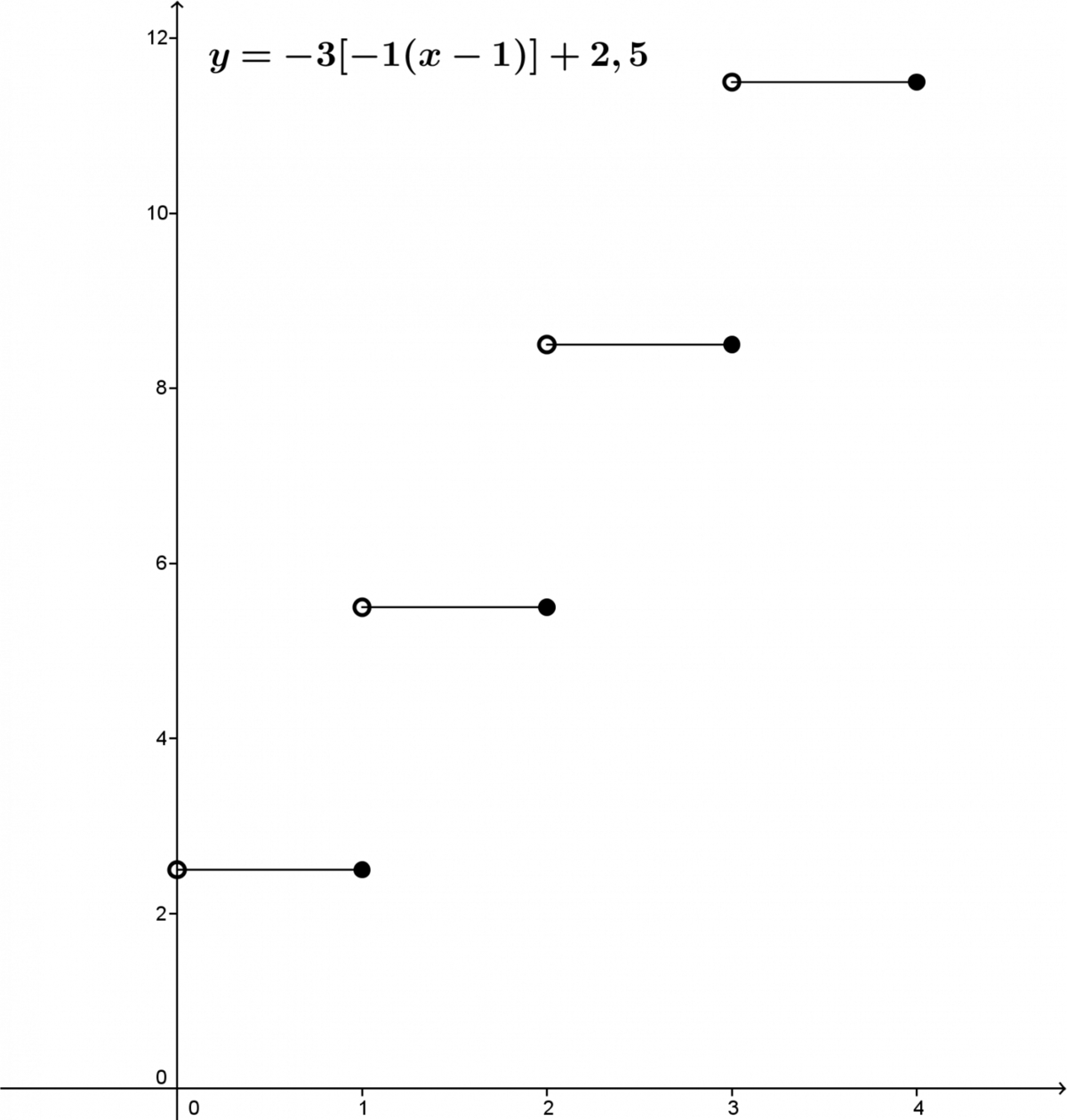
b)
On cherche la valeur de |y| lorsque |x=6.| ||\begin{align} y &= -3[-1(6-1)]+2{,}5 \\ y &= -3[-5]+2{,}5 \\ y &= -3 \times -5 + 2{,}5 \\ y &= 15 + 2{,}5 \\ y &= 17{,}5 \end{align}||
Réponse : Dominik devra payer |17{,}50\ $.|
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction partie entière de façon interactive, consulte la MiniRécup suivante.

Pour valider ta compréhension à propos de la résolution graphique de fonctions en escalier, périodiques et définies par parties de façon interactive, consulte la MiniRécup suivante.
