To solve a problem involving the greatest integer function, it is important to understand the function well. It is also important to learn how to solve the equation algebraically for a problem without context. For more details, see the following concept sheet: Solving a Step Function Equation.
Justin needs a lawyer to settle a dispute with his landlord regarding certain clauses in his lease. He contacts a lawyer specializing in property leases. The lawyer's fees are the following: for each partial or full period of |15| minutes, the lawyer charges |\$ 45|. Fortunately, taxes are included.
a) If studying the case requires |3| hours and |24| minutes, how much will it cost Justin?
b) When the case is completely settled, Justin calculates that he paid a total of |\$ 2\ 700| in fees. For how many hours did the lawyer bill him for?
Start by defining the variables.
|x|: Time billed (h)
|f(x)|: Total fees ($)
Note: For the units of |x|, we choose hours because it is the unit asked for in part b). If minutes were chosen as the unit of time instead, the equation would be different, but the ultimate result would be the same.
This situation can be drawn in a Cartesian plane.
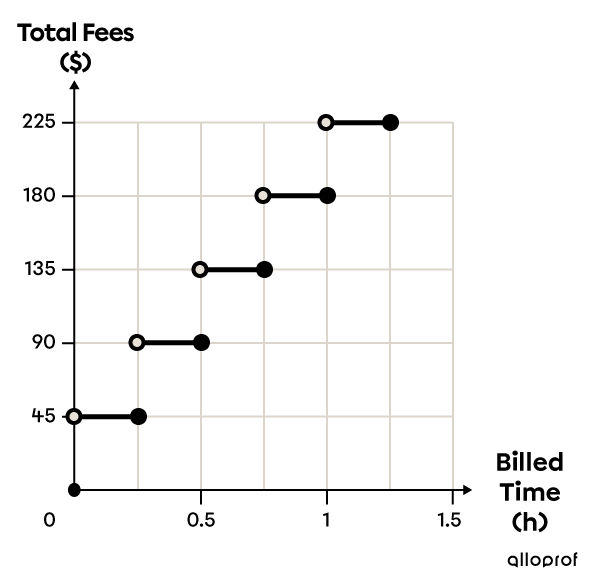
Place a point at the origin of the Cartesian plane, because if Justin does not hire the lawyer |(\text{time} = 0\ h),| the lawyer will not charge anything |(\text{fees} = \$ 0\ )!|
However, when Justin has the lawyer work on his case, even for one minute, the lawyer starts charging Justin, which is why there is a step with |y|-value |\$ 45| for the time between |0| and |0.25\ h| |(15| minutes |=| a quarter of an hour |=0.25\ h).|
Determine the value of the parameters |a| and |b| by analyzing the data.
-
Since the vertical distance between each step corresponds to an increase in the cost by |\$ 45,| this means that |{\mid}a{\mid} = 45.|
-
Since the length of each step corresponds to the time between increases in cost, which is |0.25\ h,| this means that |{\mid}b{\mid}=\dfrac{1}{0.25}=4.|
-
Each segment has an open point on the left and a closed point on the right, so |b| is negative. Therefore |{\mid}b{\mid} = -4.|
-
Given that the step function increases, the parameters |a| and |b| must have the same sign, meaning |a| is negative too. So, |a = -45.|
We can use the equation |f(x) = a[bx],| because there is a closed point at |(0.0).| Replacing the parameters |a| and |b| by the values that have been determined, we obtain the following equation for the function. ||f(x) = -45[-4x]||
Both questions can now be answered.
a)
We want the value of |f(x)| when |x = 3\ h\ 24.|
Be careful! |3\ h\ 24 \neq 3.24\ h.| The time must be converted into a decimal number as follows. ||3\ h\ 24 = 3\ h + \frac{24}{60} h = 3.4\ h||
Now |x| can be replaced by |3.4| in the equation of the function. ||\begin{align}f(x) &= -45[-4x] \\ f(3.4) &= -45[-4(3.4)] \\ &= -45[-13.6] \\ &= -45(-14) \\ &=\ \ \$ 630\end{align}||
Answer: Justin will have to pay |\$ 630| in fees.
b)
We want to find the value(s) of |x| when |f(x) = \$ 2\ 700.|
So, replace |f(x)| with |2\ 700| in the equation and isolate |x.| ||\begin{align}f(x) &= -45[-4x] \\ 2\ 700 &= -45[-4x] \\ \frac{2\ 700}{-45} &= \frac{-45[-4x]}{-45} \\ -60 &= [-4x] \\ \end{align}||
As the bracketed part is equal to a whole number, the solution can be continued.
Apply the definition of the greatest integer function. ||\begin{align}-60 = [-4x]\quad \Longleftrightarrow\quad -60 \leq\ -4&x\ < -60+1 \\ -60 \leq\ -4&x\ <-59 \\ \frac{-60}{-4}\leq\ \frac{-4}{-4}&x\ <\frac{-59}{-4} \\ 15 \geq\quad\quad &x\ >14{.}75 \end{align}||
Answer: The lawyer charged for between |14.75| and |15| hours in fees. The answer can also given as an interval: |]14.75\ ; 15]\ h.|
Dominik rents movies from his favorite video store once a week. Unfortunately, he has the annoying habit of not returning his films on time. A movie costs |\$ 2.50| on the first day. The film must be returned after one day or else he must pay a late fee of |\$ 3.00| per day.
a) Determine the equation of the function modeling this situation and draw the graph.
b) How much does Dominik have to pay if he brings back his film |6| days later?
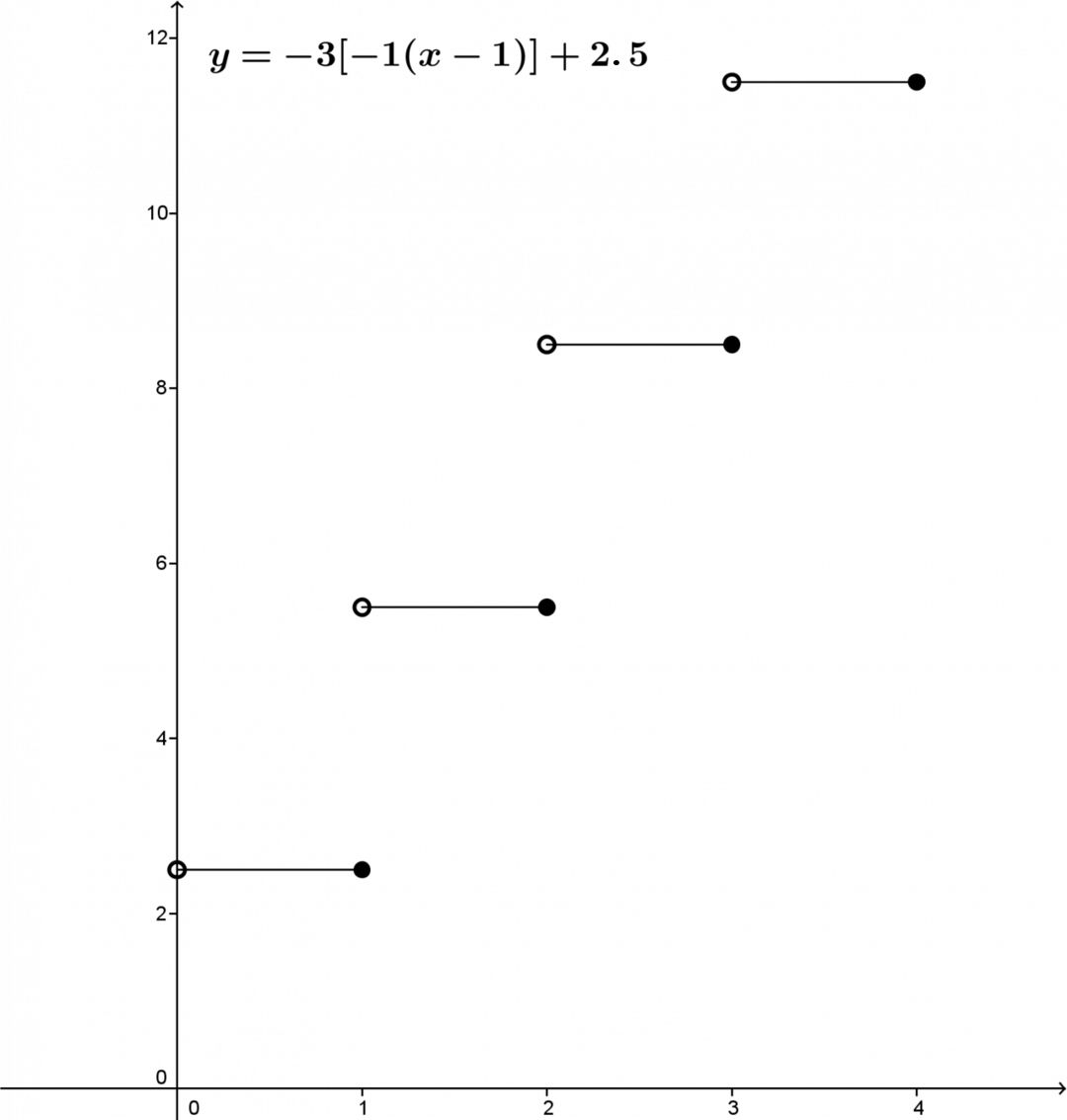
a) The function that models this situation is a step function of the form|y=a[b(x-h)]+k| where |x| is the number of days and |y| is the amount to be paid.
We can find the value of the interval |(a)|, which corresponds to the sum to be paid each day. In this case, Dominik pays |\$ 3{.}00| per day. So |a| has a value of |3.| The sign of |a| will be determined later.
In addition, the value of |b| can be found using the length of the step.
We know the formula: |\text{length of the step} = \dfrac{1}{{\mid}b{\mid}}.|
In this example, the length of the step is equal to |1| day. So, |{\mid}b{\mid} = 1.|
It only remains to determine the coordinates of a closed point to obtain some coordinates |(h,k)|. The first closed point is |(1,2.5).|
The direction of the points is closed-open (closed on the left, open on the right). So the parameter |b| must be negative. Therefore, |b=-1.|
The function is increasing, so |ab >0| meaning |a=-3.|
In summary, |a=-3,| |b=-1,| |h=1,| and |k=2.5.|
Answers: The equation is |y=-3[-1(x-1)]+2.5|, resulting in the following graph.
b)
We must find the value of |y| when |x=6.| ||\begin{align} y &= -3[-1(6-1)]+2.5 \\ y &= -3[-5]+2.5 \\ y &= -3 \times -5 + 2.5 \\ y &= 15 + 2.5 \\ y &= 17.5 \end{align}||
Answer: Dominik will have to pay |\$ 17.50.|
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction partie entière de façon interactive, consulte la MiniRécup suivante.
