Les fonctions rationnelles regroupent toutes les fonctions où l’on retrouve une fraction dans laquelle la variable indépendante |(x)| est au dénominateur.
On associe souvent la fonction rationnelle à la fonction de variation inverse (situation inversement proportionnelle). En réalité, la fonction de variation inverse est un cas particulier de l’ensemble des fonctions rationnelles.
La règle d’une fonction de variation inverse est |f(x)=\dfrac{k}{x}| où |x \neq 0.|
La forme de base d’une fonction rationnelle est la suivante. ||f(x)=\dfrac{1}{x}||où |x \neq 0|
Le graphique de la fonction rationnelle de base est composé de 2 courbes, appelées hyperboles, qui se rapprochent des 2 axes sans y toucher.
-
Une courbe passe par le point |(1,1),| l’autre par le point |(-1,-1).|
-
Le domaine est |\mathbb{R}\backslash \{0\}.|
-
L’image est |\mathbb{R}\backslash \{0\}.|
-
La fonction est décroissante sur l’intervalle |]-\infty,0[,| puis sur l’intervalle |]0,+\infty[.|
-
La fonction de base ne possède pas d’ordonnée à l’origine ni de zéro.
-
La fonction ne possède pas de maximum ni de minimum.
-
La fonction possède 2 asymptotes perpendiculaires : |x=0| et |y=0.|
-
La fonction est négative sur l’intervalle |]-\infty,0[| et est positive sur l’intervalle |]0,+\infty[.|

La fonction rationnelle transformée peut s’écrire de 2 façons différentes.
La forme canonique
||f(x)=\dfrac{a}{b(x-h)}+k||où |b\neq 0|
La forme générale
||f(x)=\dfrac{a_1 x+b_1}{a_2 x+b_2}||où |a_2 \neq 0|
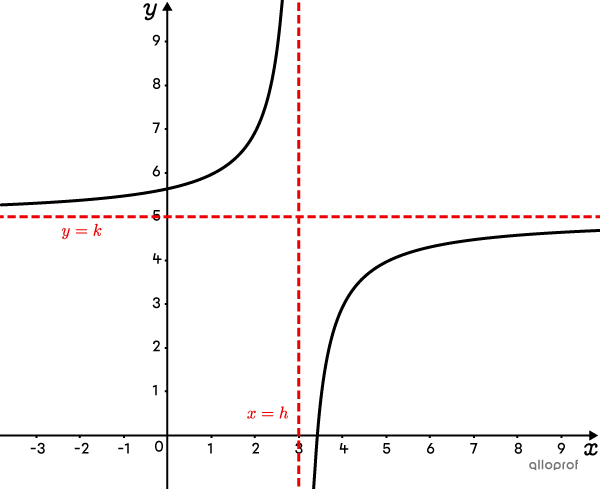
Le graphique de la fonction rationnelle transformée est composé de 2 courbes, appelées hyperboles, qui se rapprochent des 2 asymptotes sans y toucher.
-
Le domaine est |\mathbb{R}\backslash \{h\}.|
-
L’image est |\mathbb{R}\backslash \{k\}.|
-
Lorsque |ab>0,| la fonction est décroissante sur l’intervalle |]-\infty,h[,| puis sur l’intervalle |]h,+\infty[.|
-
Lorsque |ab<0,| la fonction est croissante sur l’intervalle |]-\infty,h[,| puis sur l’intervalle |]h,+\infty[.|
-
La fonction possède une ordonnée à l’origine si |h\neq 0| et un zéro si |k \neq 0.|
-
La fonction ne possède pas de maximum ni de minimum.
-
La fonction possède 2 asymptotes perpendiculaires : |x=h| et |y=k.|
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction rationnelle de façon interactive, consulte la MiniRécup suivante.
