Pour résoudre un problème où intervient une fonction valeur absolue, il faut connaitre tous les rouages de cette fonction et il faut connaitre les façons de résoudre une équation hors contexte. Tu peux consulter la fiche suivante au besoin : Résoudre une équation ou une inéquation de valeur absolue.
La température dans une journée varie souvent comme une fonction valeur absolue. C’est le cas pour cette splendide journée ensoleillée de novembre! Le matin, à 6 h, la température était de -6°C. Quand le soleil s’est mis à briller, la température s’est mise à monter à un rythme régulier jusqu’à atteindre un maximum de 9°C à 16 h. À partir de ce moment-là, la température s’est mise à redescendre jusqu’à minuit en suivant le même rythme que sa montée.
a) Quelle était la température à midi et à minuit?
b) À quel(s) moment(s) la température était-elle au point de congélation?
-
Définir les variables
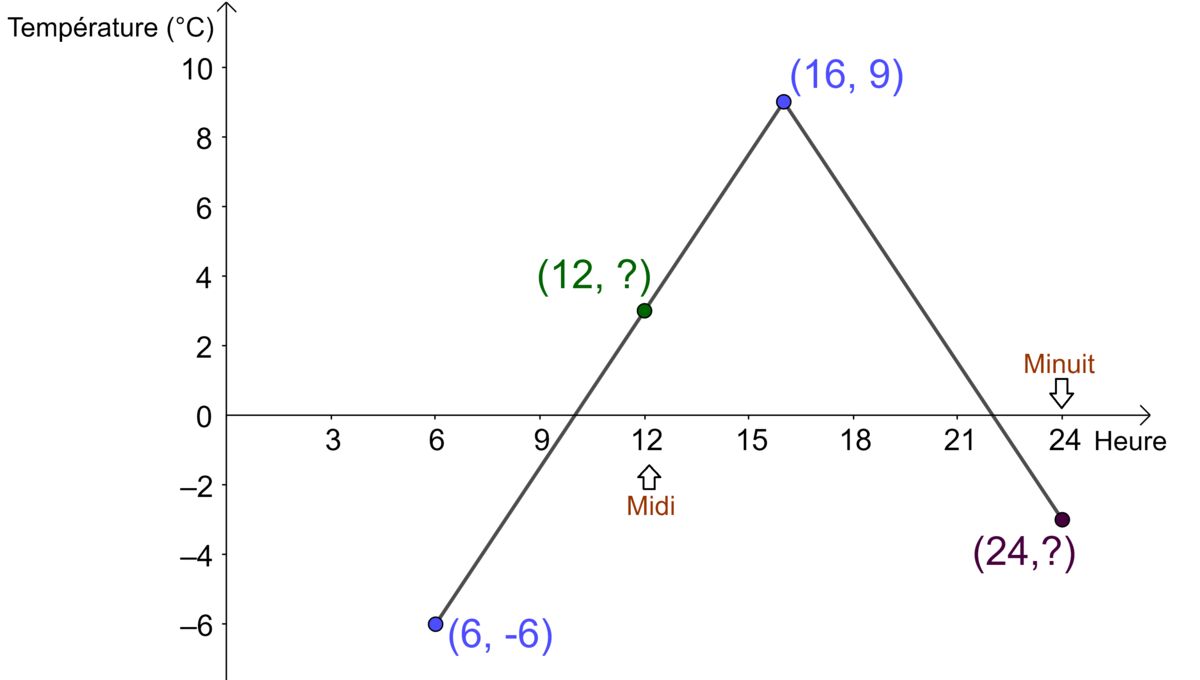
Attention! Ici, il faut être précis pour définir |x.| Il y a deux possibilités : |x| peut être l’heure de la journée ou le temps écoulé depuis 6 h du matin. Si |x| est l’heure de la journée et qu'on ne sait pas ce qui se passe avant 6 h, le graphique aurait l’air de ceci :
Si |x| était le temps écoulé depuis 6 h, alors à 16 h, |x=10| et non |16.| Aussi, à midi, |x=12-6=6| et à minuit, |x=24-6=18.| Le point |(6,-6)| deviendrait |(0,-6)| et serait donc notre ordonnée à l’origine. Le graphique aurait l’air de ceci :

C’est avec ce dernier graphique que nous allons faire le reste du problème. Donc, les variables sont :
|\color{blue}{x}| : Temps écoulé depuis 6 h
|\color{magenta}{f(x)}| : Température (°C)
-
Trouver la règle
On mentionne dans l'énoncé qu'il s'agit d'une fonction valeur absolue mais, même sans cette précision, on aurait pu le déduire parce qu'on dit que les rythmes de diminution et d'augmentation sont égaux. Si ce n'était pas le cas, nous aurions eu affaire à une fonction définie par parties.
Pour trouver la règle, nous allons utiliser la forme canonique (avec les paramètres |\color{purple}{a}|, |\color{red}{h}| et |\color{green}{k}|). D’abord, nous allons remplacer |\color{red}{h}| et |\color{green}{k}| par les coordonnées du sommet |(\color{red}{10},\color{green}{9}).| Puis, nous allons remplacer les variables |\color{blue}{x}| et |\color{magenta}{f(x)}| par les coordonnées d’un point autre que le sommet. Dans notre cas, nous allons utiliser le point |(\color{blue}{0},\ \color{magenta}{-6}).| ||\begin{align}\color{magenta}{f(x)}&=\color{purple}{a} \mid \color{blue}{x}-\color{red}{h} \mid+\ \color{green}{k}\\ \color{magenta}{f(x)}&=\color{purple}{a} \mid \color{blue}{x}-\color{red}{10} \mid+\ \color{green}{9}\\ \color{magenta}{-6}&=\color{purple}{a} \mid \color{blue}{0}-\color{red}{10} \mid+\ \color{green}{9}\\ -15 &=\color{purple}{a} \mid -\color{red}{10}\ \mid\\ -15 &=10\color{purple}{a}\\ \color{purple}{-1{,}5}&=\color{purple}{a}\end{align}||La règle de la fonction est donc : ||\color{magenta}{f(x)}=\color{purple}{-1{,}5} \mid \color{blue}{x}-\color{red}{10} \mid+\ \color{green}{9}||Remarque : La valeur de |\color{purple}{a}| est négative, ce qui est cohérent avec le graphique : notre fonction possède un maximum et le V est ouvert vers le bas. De plus, la valeur 1,5 indique les rythmes d'augmentation (1,5 °C/heure) et de diminution (-1,5 °C/heure) de la température.
a) Pour trouver la température à minuit, il faut remplacer |\color{blue}{x}| par |\color{blue}{18}| et isoler |\color{magenta}{f(x)}.| ||\begin{align} \color{magenta}{f(x)}&=-1{,}5 \mid \color{blue}{x} -10 \mid+\ 9\\ \color{magenta}{f(x)}&=-1{,}5 \mid \color{blue}{18} -10 \mid+\ 9\\ \color{magenta}{f(x)}&=-1{,}5 \mid 8\mid+\ 9\\ \color{magenta}{f(x)}&=-1{,}5 (8)+9\\ \color{magenta}{f(x)}&=-12+9\\ \color{magenta}{f(x)}&=-3\\\end{align}|| Pour trouver la température à midi, il faut remplacer |\color{blue}{x}| par |\color{blue}{6}| et isoler |\color{magenta}{f(x)}.| ||\begin{align} \color{magenta}{f(x)}&=-1{,}5 \mid \color{blue}{x} -10 \mid+\ 9\\ \color{magenta}{f(x)}&=-1{,}5 \mid \color{blue}{6} -10 \mid+\ 9\\ \color{magenta}{f(x)}&=-1{,}5 \mid -4\mid+\ 9\\ \color{magenta}{f(x)}&=-1{,}5 (4)+9\\ \color{magenta}{f(x)}&=-6+9\\ \color{magenta}{f(x)}&=3\\\end{align}||
Réponses : À midi, la température extérieure était de 3 °C. À minuit, elle était de -3 °C.
b) Pour trouver à quel(s) moment(s) la température était au point de congélation, il faut comprendre que celui-ci correspond à |0|°C. Il faut donc remplacer |\color{magenta}{f(x)}| par |\color{magenta}{0}| et isoler |x.| Attention! Si on se fie au graphique, on devrait trouver deux moments où la température était de |0|°C, soit une première fois pendant que la température augmentait, puis une deuxième fois en soirée alors que la température redescendait. ||\begin{align} \color{magenta}{f(x)}&=-1{,}5 \mid \color{blue}{x} -10 \mid+\ 9\\ \color{magenta}{0}&=-1{,}5 \mid \color{blue}{x} -10 \mid+\ 9\\ -9&=-1{,}5 \mid \color{blue}{x}-10\mid \\ 6&=\mid \color{blue}{x}-10\mid \\ \end{align}|| À partir d'ici, on applique la définition de la valeur absolue, ce qui nous donne 2 équations qu'on doit résoudre. ||\begin{align}\color{blue}{x}-10&=6\ \ \ \text{si } x>10\ \ \ \ \ \ \ \text{et } &\color{blue}{x}-10&=-6 \text{ si } x<10\\ \Rightarrow \color{blue}{x_2}&=16 \text{ h} &\Rightarrow \color{blue}{x_1}&=4 \text{ h} \end{align}|| Attention! Il faut se rappeler qu'on avait défini notre variable |\color{blue}{x}| comme étant le temps écoulé depuis 6 h. Donc, pour trouver les heures où la température était au point de congélation, il faut ajouter |6| à nos deux solutions. ||\begin{align}\color{blue}{x_1}&=4\ \ +6=10 \text{ h}\\ \color{blue}{x_2}&=16+6=22 \text{ h}\end{align}||
Réponse : La température extérieure était au point de congélation à 10 h du matin et à 10 h du soir (22 h).
Dans l'exemple précédent, nous n'avions affaire qu'à des équations et non à des inéquations. Une dernière sous-question qui aurait fait appel aux inéquations aurait pu être : « Pendant quel intervalle de temps la température était-elle supérieure à 5 °C ? » Pour savoir comment répondre à ce genre de question, vous pouvez consulter la fiche suivante : Résoudre une inéquation contenant une valeur absolue.
Voici maintenant 3 vidéos qui donnent d'autres exemples de problèmes impliquant une valeur absolue.
Pour valider ta compréhension à propos de la résolution de problèmes impliquant la fonction valeur absolue de façon interactive, consulte la MiniRécup suivante.
