En géométrie analytique, un demi-plan représente l'ensemble-solution d'une inéquation du premier degré à deux variables.
Un ensemble-solution est l'ensemble des valeurs vérifiant une équation ou une inéquation.
Les concepts de demi-plan et d'inéquation du premier degré à deux variables sont étroitement liés lorsqu'il est question de géométrie analytique. En fait l'un est la représentation graphique de l'autre.
Le demi-plan peut être vu comme l'une des deux portions d'un plan délimité par une droite nommée droite frontière.
Une droite frontière est une droite qui délimite l'ensemble-solution d'une inéquation.
Il existe deux types de droite frontière :
-
Si l'inégalité n'est pas stricte (|\leq| ou |\geq|), la droite frontière fera partie de l'ensemble-solution et on la représentera par un trait plein.
-
Si l'inégalité est stricte (|<| ou |>|), la droite frontière ne fera pas partie de l'ensemble-solution et on la représentera par un trait pointillé.
Le demi-plan suivant représente l'ensemble-solution de l'inéquation |y>3x.|
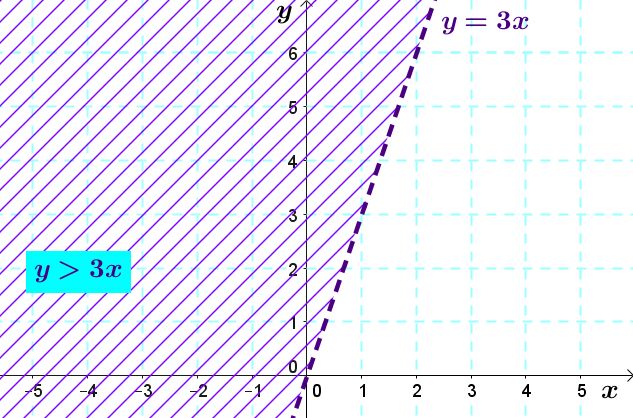
On remarque ici que la droite frontière |y=3x| est pointillée. Ceci est dû au fait que le signe d'inégalité de l'inéquation (|>|) est strict.
On aura cependant un trait plein pour la droite frontière de l'ensemble-solution de l'inéquation |y\geq3x.|
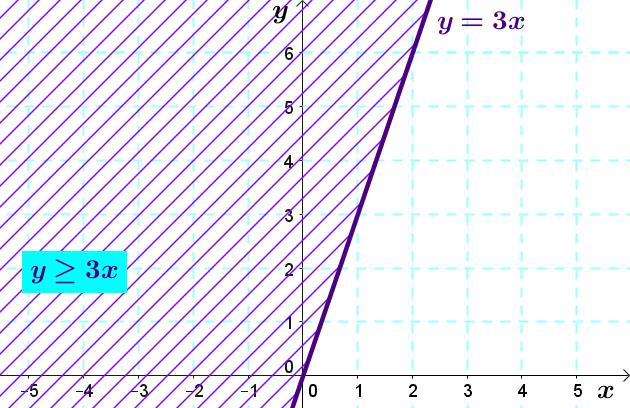
Un demi-plan peut aussi servir à représenter une inéquation du premier degré à une variable.
Lorsque l'inéquation comprend seulement :
-
la variable indépendante |(y),| on aura une droite frontière horizontale;
-
la variable dépendante |(x),| on aura une droite frontière verticale.
-
Le demi-plan suivant représente l'ensemble-solution de l'inéquation |y\leq4.|
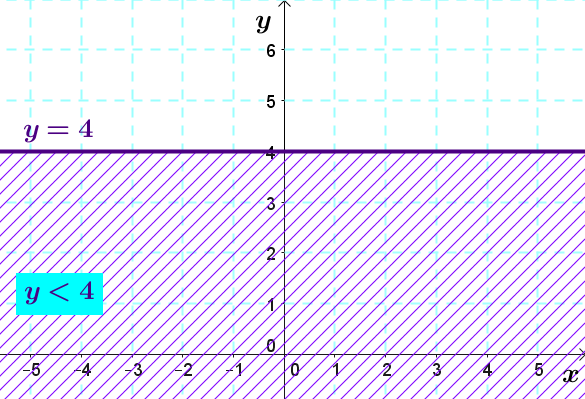
L'ensemble-solution comprend tous les points dont la coordonnée en |y| est plus petite ou égale à |4.|
-
Le demi-plan suivant représente l'ensemble-solution de l'inéquation |x>-2.|
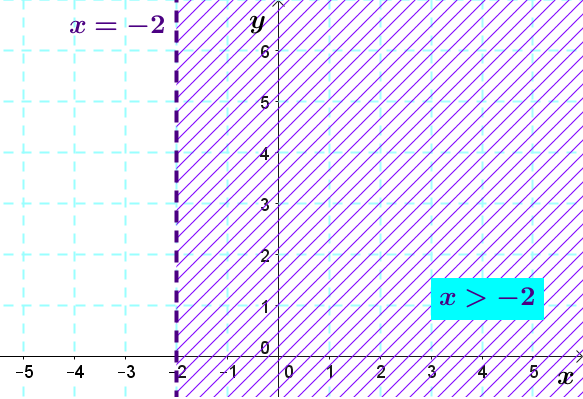
L'ensemble-solution comprend tous les points dont la coordonnée en |x| est strictement plus grande que |-2.|
Dans certaines situations, il peut être demandé de représenter graphiquement l'ensemble-solution d'une inéquation du premier degré à deux variables. Voici comment procéder.
-
Écrire l'inéquation en isolant la variable dépendante
|y>ax+b|, par exemple -
Tracer la droite frontière d'équation |y=ax+b|
Cette droite sera pointillée ou pleine selon le signe de l'inéquation. -
Hachurer le demi-plan :
- au-dessus de la droite frontière si le signe d'inégalité est |>| ou |\geq|
- au-dessous de la droite frontière si le signe d'inégalité est |<| ou |\leq|
Attention, pour utiliser cette technique, la variable dépendante doit être isolée à gauche de l'inégalité.
Il est possible de valider si nous avons hachuré le bon demi-plan en y choisissant un point-test. Il suffit de remplacer les variables de l'inéquation par les coordonnées de ce point. Si ces coordonnées vérifient l'inéquation, nous avons hachuré le bon demi-plan.
Tracer le demi-plan correspondant à l'ensemble-solution de l'inéquation |4x+2y\leq 6.|
1. Écrire l'inéquation sous sa forme fonctionnelle
||\begin{align} 4x \color{red}{-4x} + 2y &\leq 6 \color{red}{-4x} \\ 2y \color{red}{\div 2} &\leq (6 - 4x) \color{red}{\div 2} \\ y &\leq - 2x + 3 \end{align}||
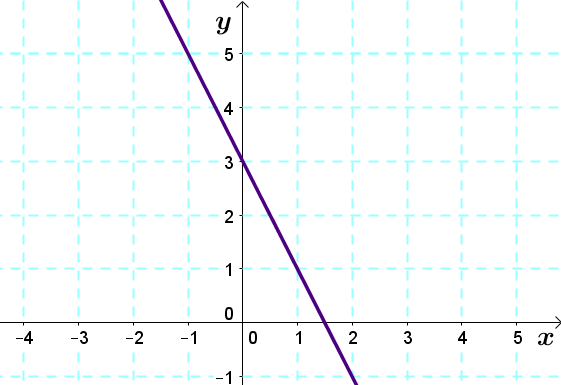
2. Tracer la droite frontière d'équation |y=-2x+3|
Comme le signe d'inégalité est |\leq,| cette droite sera représentée par un trait plein.
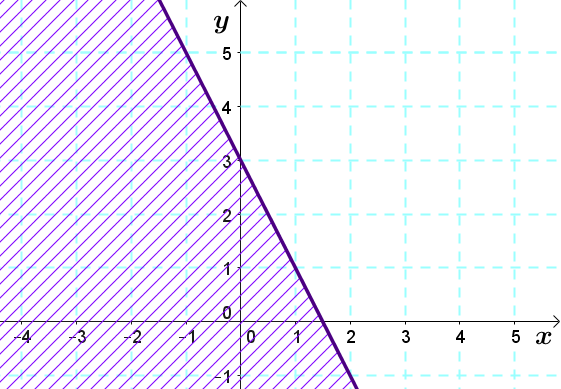
3. Hachurer le demi-plan correspondant à l'ensemble-solution de l'inéquation
Comme le signe d'inégalité de l'inéquation est |\leq ,| il faut hachurer au-dessous de la droite frontière.
Validons maintenant notre tracé à l'aide d'un point-test. Prenons le point |(-1,2)| faisant partie de la région hachurée et remplaçons les variables de l'inéquation de départ par ses coordonnées. ||\begin{align} 4x + 2y &\leq 6 \\ 4(\color{blue}{-1})+2(\color{blue}{2}) &\leq6 \\ -4 + 4 &\leq 6 \\ 0 &\leq 6 \Longrightarrow \text{VRAI} \end{align}||
Les coordonnées du point-test vérifie l'inéquation. Nous pouvons donc affirmer que le demi-plan ci-haut représente bien l'ensemble-solution de l'inéquation |4x+2y\leq 6.|
Si on multiplie ou on divise par un nombre négatif lorsqu'on manipule l'inéquation pour isoler la variable dépendante, il faut changer le sens du signe d'inégalité.
Pour être bien certain de ne pas faire d'erreur dans les manipulations, il peut être bon de revoir la notion d'inéquation.
Parfois, il est possible qu'on demande de déterminer la représentation algébrique d'un demi-plan. Cette représentation algébrique aura la forme d'une inéquation à deux variables. Voici les étapes de la démarche permettant d'y arriver.
-
Trouver l'équation de la droite frontière
-
Choisir le bon signe d'inégalité selon la région hachurée et l'allure de la droite frontière
L'astuce du point-test fonctionne toujours pour valider si nous avons choisi le bon signe d'inégalité. Il suffit de choisir un point appartenant à la région hachurée et de remplacer les variables de l'inéquation trouvée par ses coordonnées. Si ces coordonnées vérifient l'inéquation, nous avons choisi le bon sens pour le signe d'inégalité.
Détermine l'inéquation dont l'ensemble-solution correspond au demi-plan ci-dessous.
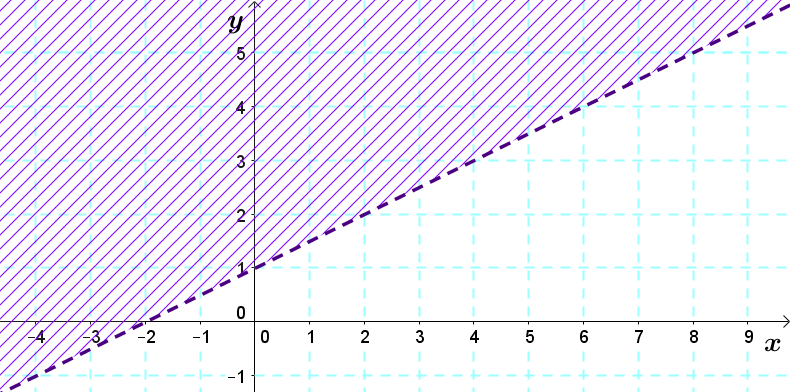
1. Trouver l'équation de la droite frontière
À l'aide du graphique, il est possible de déterminer que l'ordonnée à l'origine de la droite frontière est |1.| On peut ensuite calculer la pente à l'aide de deux points appartenant à la droite. Prenons les points |(2,2)| et |(4,3).| ||\begin{align}a=\displaystyle \frac{\triangle y}{\triangle x}&=\frac{y_2-y_1}{x_2-x_1}\\ &=\displaystyle \frac{3-2}{4-2}=0{,}5\end{align}||L'équation de la droite frontière est donc |y=0{,}5x+1|
2. Choisir le bon signe d'inégalité
Comme la région hachurée se retrouve au-dessus de la droite, il faut utiliser le signe |>| ou |\geq.|
De plus, puisque la droite frontière du graphique est pointillée, on doit choisir un signe d'inégalité stricte. Le bon signe d'inégalité est donc |>.|
L'inéquation recherchée est |y>0{,}5x+1|
Il est possible de valider l'inéquation à l'aide d'un point-test. Prenons le point |(1,3)| qui fait partie de la région hachurée du graphique et remplaçons les variables de l'inéquation par ses coordonnées. ||\begin{align}y&>0{,}5x+1\\ \color{blue}{3}&>0{,}5(\color{blue}{1})+1\\ 3&>1{,}5\end{align}||L'inéquation est vérifiée, nous avons choisi le bon sens pour le signe d'inégalité.